testul rădăcinilor raționale (cunoscut și sub denumirea de teorema zerourilor raționale) ne permite să găsim toate rădăcinile raționale posibile ale unui polinom. Să presupunem că a este rădăcina polinomului p \ left (x \right) care înseamnă P\left( a \right) = 0. Cu alte cuvinte, dacă înlocuim a în polinomul p \ left (x \right) și obținem zero, 0, înseamnă că valoarea de intrare este o rădăcină a funcției.dar cum găsim lista posibilă de rădăcini raționale? Iată cum funcționează pe scurt!,
Cheie Idei de Rădăcini Raționale Test
să Presupunem că avem un polinom P\left( x \right) cu coeficienti și o constantă diferită de zero termen:
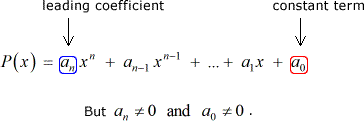
Apoi fiecare rațională rădăcină de P\left( x \right) este de forma:
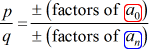
Cel mai bun mod de a învăța această metodă este de a lua o privire la câteva exemple!,
Exemple de cum să găsiți rădăcinile raționale ale unui polinom folosind testul rădăcinilor raționale
Exemplul 1: găsiți rădăcinile raționale ale polinomului de mai jos folosind testul rădăcinilor raționale.
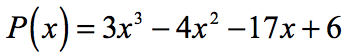
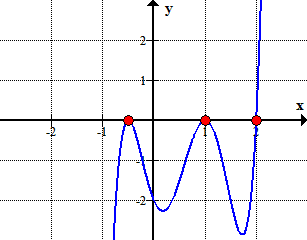
Găsirea rațională rădăcini (de asemenea, cunoscut sub numele de rațională zerouri) de un polinom este aceeași ca și găsirea raționale x-interceptează.
- începeți prin identificarea termenului constant a0 și a coeficientului principal an.,
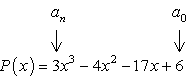
- Determinarea factori pozitivi și negativi din fiecare.
Factori de termen constant, {a_0} = 6\,\,:\,\, \pm \,\left( {1,2,3,6} \right)
Factori de conducere termen, {a_n} = 3\,\,:\,\, \pm \,\left( {1,3} \right)
- Scrie în jos lista de posibile rădăcini raționale prin găsirea {p \peste q} care este pur și simplu raportul dintre factorii de constante pe termen lung și de conducere pe termen lung. Asigurați-vă că urmăriți combinațiile posibile.,
acesta este modul în care o fac. Iau fiecare numărător și îl împart cu toți numitorii. Apoi trec la următorul numărător și împart din nou cu toți numitorii. Repet acest proces până când am trecut prin toți numărătorii. Acest lucru asigură că am acoperit toate combinațiile posibile.
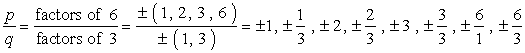
MARE Atenție: După ce ați scrie în jos toate combinațiile, simplificarea fracțiilor în scopul de a scăpa de duplicate.,
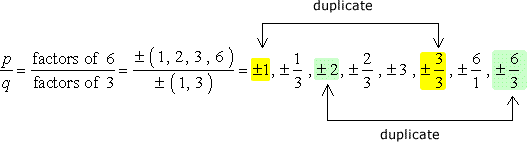
Deci, acestea sunt numerele fără duplicate că vom verifica cât posibil rădăcini. Avem doisprezece (12) posibili candidați pentru a verifica.
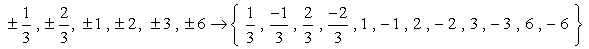
- Amintiți-vă că, dacă a este o rădăcină a polinomului P\left( x \right), atunci P\left( o \right) = 0. Acum, să verificăm fiecare număr.,
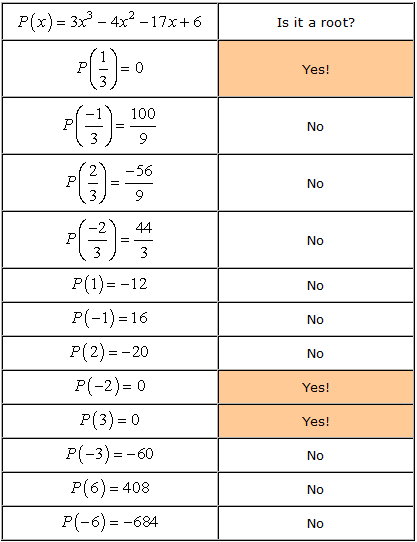
- Therefore, the rational roots of the polynomial
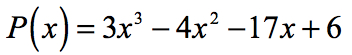
are

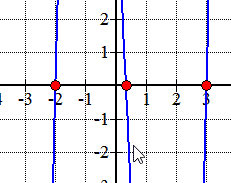
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
Exemplu 2: Găsi rațional rădăcinile polinomului de mai jos, folosind Rațional Rădăcini de Testare.
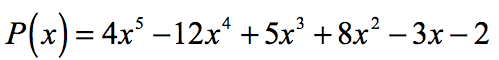
termenul constant este a0 = -2 și posibil de factori sunt p = ± 1, ± 2. Pentru coeficientul principal, avem an = 4, iar factorii săi sunt q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
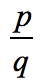
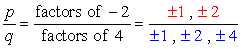
Write down all possible
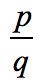
combinations:
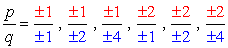
- Simplify each fraction to eliminate duplicates or identical values., Iată lista noastră nouă și îmbunătățită!
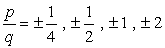
- ca urmare a plus sau minus considerare de fiecare număr, vom avea opt (8) candidați posibil ca rădăcinile acestui polinom.
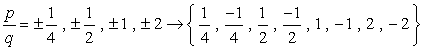
Dacă vă conectați în fiecare valoarea a dat polinom și devine zero, ceea ce înseamnă că numărul substituit este o rădăcină!, Încercați acest lucru pe hârtie și ar trebui să fiți convins că există doar trei valori care satisfac această condiție.
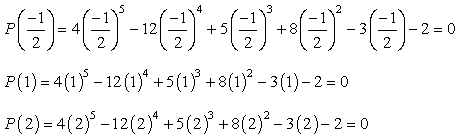
prin Urmare, rațional rădăcinile polinomului
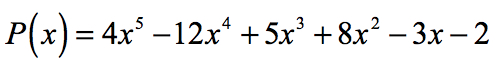
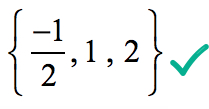
Grafic, se arată că polinom atinge sau trece axa x la aceste rădăcini determinate de rațională rădăcini de testare.,