De Rational Roots Test (ook bekend als Rational nullen stelling) stelt ons in staat om alle mogelijke rationale wortels van een veelterm te vinden. Stel dat a wortel is van de veelterm P\left (x \ right) dat betekent P\left( a \right) = 0. Met andere woorden, als we a vervangen door de veelterm P\links( x \rechts) en nul, 0 krijgen, betekent dit dat de invoerwaarde een wortel van de functie is.
maar hoe vinden we de mogelijke lijst van rationele wortels? Hier is hoe het werkt in een notendop!,
Belangrijke Ideeën van Rationele Wortels Test
Stel we hebben een aantal polynoom P\left( x \right) gehele coëfficiënten en een andere constante term:
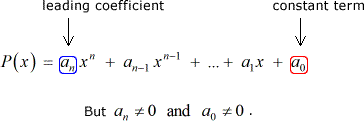
Vervolgens elke rationele wortel van P\left( x \right) is van de vorm:
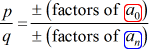
De beste manier om te leren van deze methode is om een kijkje te nemen naar enkele voorbeelden!,
voorbeelden van hoe de rationale wortels van een veelterm te vinden met behulp van de Rational Roots Test
Voorbeeld 1: Zoek de rational roots van de veelterm hieronder met behulp van de Rational Roots Test.
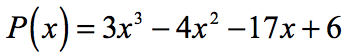
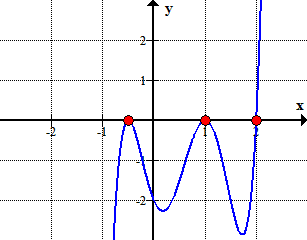
het vinden van de rationale wortels (ook wel rationale nullen genoemd) van een veelterm is hetzelfde als het vinden van de rationale x-intercepts.
- begin met het identificeren van de constante term a0 en de leidende coëfficiënt an.,
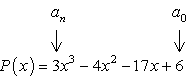
- Bepaal de positieve en negatieve factoren van elk.
factoren van constante term, {a_0} = 6\,\,:\,\, \pm \, \ left ({1,2,3,6} \right)
factoren van voorloopterm, {a_n} = 3\,\,:\,\, \pm \, \ left ({1,3} \right)
- noteer de lijst van de mogelijke rationele wortels door {p \over q} te vinden, wat gewoon de verhouding is van de factoren van de constante term en de leidende term. Zorg ervoor dat u de mogelijke combinaties bijhoudt.,
Dit is hoe ik het doe. Ik neem elke teller en deel het door alle noemers. Dan ga ik door naar de volgende teller en weer delen door alle noemers. Ik blijf dit proces herhalen totdat ik alle tellers heb doorlopen. Dit zorgt ervoor dat we alle mogelijke combinaties hebben behandeld.
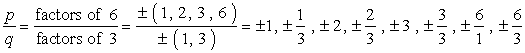
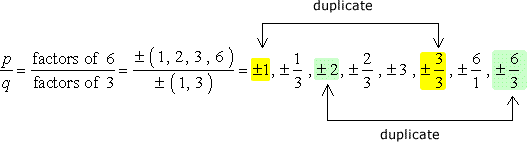
grote Waarschuwing: nadat u alle combinaties hebt opgeschreven, vereenvoudig de breuken om duplicaten te verwijderen.,
Dit zijn de getallen zonder duplicaten die we zullen controleren als mogelijke roots. We hebben twaalf (12) mogelijke kandidaten om te controleren.
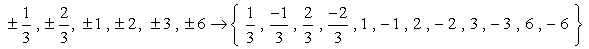
- onthoud dat als a een wortel is van de veelterm P\left( x \right), dan P\left( a \right) = 0. Laten we elk nummer controleren.,
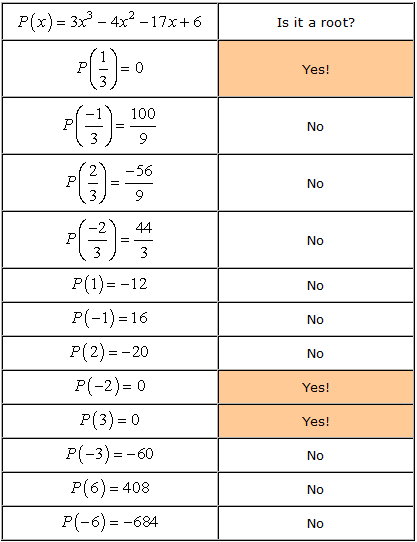
- Therefore, the rational roots of the polynomial
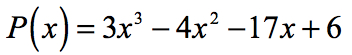
are

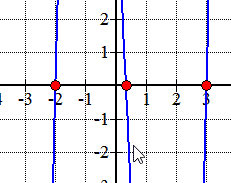
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
Voorbeeld 2: Zoek de rationale wortels van de veelterm hieronder met behulp van Rational Roots Test.
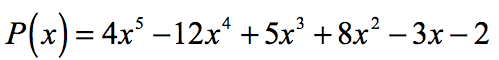
de constante term is a0 = -2 en de mogelijke factoren zijn P = ± 1, ± 2. Voor de belangrijkste coëfficiënt hebben we an = 4 en de factoren zijn q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
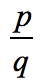
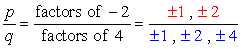
Write down all possible
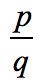
combinations:
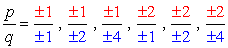
- Simplify each fraction to eliminate duplicates or identical values., Hier is onze nieuwe en verbeterde lijst!
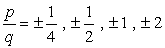
- vanwege de plus-of minafweging van elk getal, zullen we acht (8) mogelijke kandidaten hebben als de wortels van deze veelterm.
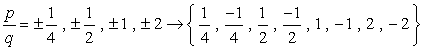
Als u elke waarde op de gegeven veelterm aansluit en nul krijgt, betekent dit dat het getal dat u hebt vervangen een root is!, Probeer dit op papier en je moet ervan overtuigd zijn dat er slechts drie waarden zijn die aan deze voorwaarde voldoen.
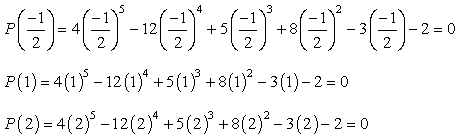
Daarom, de rationele wortels van de polynoom
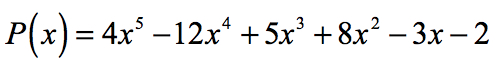
zijn
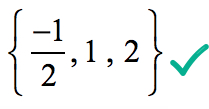
Grafisch, blijkt dat de veelterm raakt of kruist de x-as op die wortels bepaald door rationele wortels test.,