Den Rasjonelle Røtter Test (også kjent som Rasjonell Nuller Teorem) gjør det mulig for oss å finne alle mulig rasjonell røttene til et polynom. Anta at a er en rot i polynomet P\left( x \right) som betyr P\venstre( a \right) = 0. Med andre ord, hvis vi erstatter en i polynom P\left( x \right) og få null, 0, betyr det at input-verdien er du en rot av funksjon.
Men hvordan skal vi finne mulige liste over rasjonell røtter? Her er hvordan det fungerer i et nøtteskall!,
– Tasten Ideer av Rasjonell Røtter Test
la oss Anta at vi har noen polynom P\left( x \right) med heltall koeffisienter og en ikke-null konstant sikt:
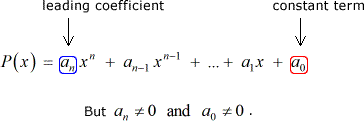
Deretter hver rasjonell root P\left( x \right) er på formen:
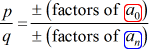
Den beste måten å lære denne metoden er å ta en titt på noen eksempler!,
Eksempler på Hvordan å Finne den Rasjonelle Røttene til et Polynom med Rasjonell Røtter Test
Eksempel 1: Finn den rasjonelle røtter i polynomet nedenfor ved bruk av den Rasjonelle Røtter Test.
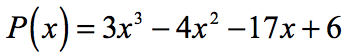
Finne den rasjonelle røtter (også kjent som rasjonell nuller) av et polynom er det samme som å finne den rasjonelle x-avskjærer.
- Start med å identifisere konstant sikt a0 og fører koeffisient en.,
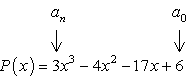
- Bestemme de positive og negative faktorer av hver.
Faktorer konstant sikt, {a_0} = 6\,\,:\,\, \pm \,\left( {1,2,3,6} \right)
Faktorer som fører sikt, {a_n} = 3\,\,:\,\, \pm \,\left( {1,3} \right)
- Skriv ned en liste over mulig rasjonell røtter ved å finne {p \over q} som er rett og slett forholdet mellom faktorer av konstant sikt og ledende sikt. Sørg for at du holde oversikt over mulige kombinasjoner.,
Dette er hvordan jeg gjør det. Jeg tar hver teller og dele det med alle denominators. Da skal jeg gå videre til neste teller og igjen dele med alle denominators. Jeg holder gjenta denne prosessen til jeg har gått gjennom alle numerators. Dette sikrer at vi har dekket alle mulige kombinasjoner.
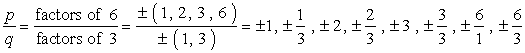
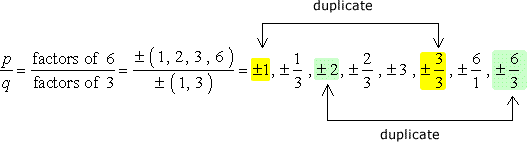
STOR Forsiktig: Når du skriver ned alle kombinasjoner, forenkle brøker for å bli kvitt duplikater.,
Så dette er tallene uten duplikater som vi ser som mulige røtter. Vi har tolv (12) mulige kandidater for å sjekke.
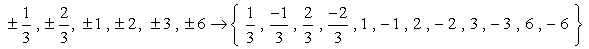
- Husk at hvis a er en rot i polynomet P\left( x \right), deretter P\venstre( a \right) = 0. Nå, la oss sjekke hvert nummer.,
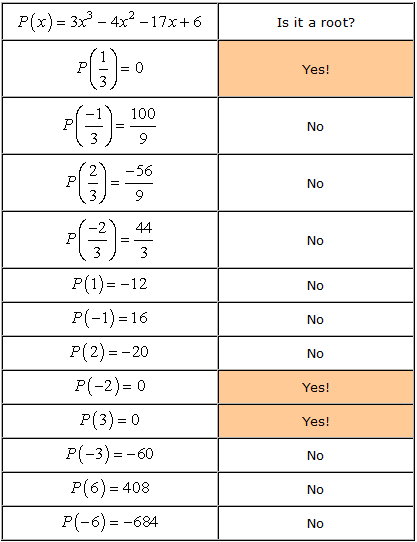
- Therefore, the rational roots of the polynomial
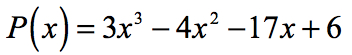
are

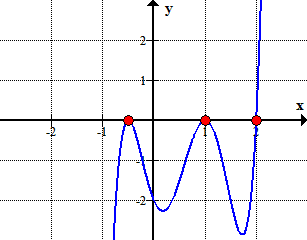
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
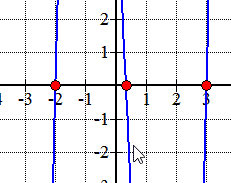
Eksempel 2: Finn rasjonell røtter i polynomet nedenfor ved hjelp av Rasjonell Røtter Test.
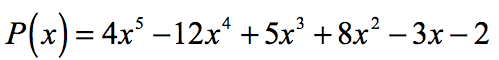
Den konstante sikt er a0 = -2 og dens mulige faktorer er p = ± 1, ± 2. For de ledende koeffisienten, har vi en = 4 og faktorer er q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
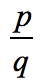
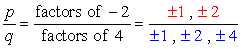
Write down all possible
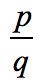
combinations:
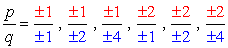
- Simplify each fraction to eliminate duplicates or identical values., Her er vår nye og forbedrede liste!
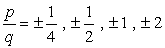
- på Grunn av pluss-eller minus-vurdering av hvert nummer vil vi ha åtte (8) mulige kandidater til røttene av denne polynom.
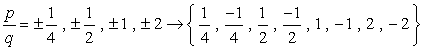
Hvis du plugger i hver verdi til gitt polynom og får null, betyr det at antallet du byttet ut er en rot!, Prøv dette på papiret, og du skal bli overbevist om at det er bare tre verdier tilfredsstillende denne tilstanden.
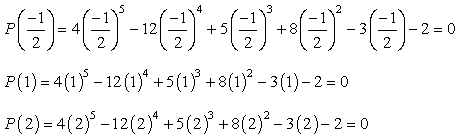
Derfor, den rasjonelle røtter i polynomet
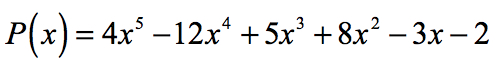
er
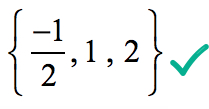
Grafisk, for det viser at polynom berører eller krysser x-aksen på de røttene bestemt av rasjonell røtter test.,