Il test delle radici Razionali (noto anche come Teorema degli zeri razionali) ci consente di trovare tutte le possibili radici razionali di un polinomio. Supponiamo che a sia la radice del polinomio P \ left (x \ right) che significa P \ left (a \right) = 0. In altre parole, se sostituiamo a nel polinomio P \ left(x \ right) e otteniamo zero, 0, significa che il valore di input è una radice della funzione.
Ma come troviamo la possibile lista di radici razionali? Ecco come funziona in poche parole!,
Idee Chiave di Radici Razionali Test
Supponiamo di avere qualche polinomio P\left( x \right) con coefficienti interi e una costante diversa da zero termine:
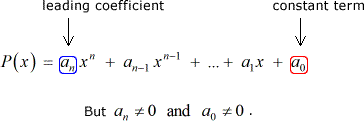
Poi ogni razionale radice di P\left( x \right) è della forma:
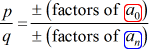
Il modo migliore per imparare questo metodo è quello di prendere uno sguardo ad alcuni esempi!,
Esempi di come trovare le radici razionali di un polinomio usando il Rational Roots Test
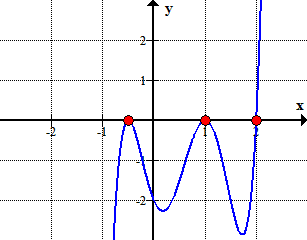
Esempio 1: Trova le radici razionali del polinomio sotto usando il Rational Roots Test.
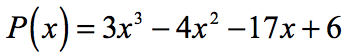
Trovare le radici razionali (note anche come zeri razionali) di un polinomio equivale a trovare gli x-intercetti razionali.
- Inizia identificando il termine costante a0 e il coefficiente iniziale an.,
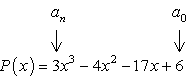
- Determinare i fattori negativi che positivi di ciascuno.
Fattori di termine costante, {a_0} = 6\,\,:\,\, \pm \,\left( {1,2,3,6} \right)
Fattori di condurre a termine, {a_n} = 3\,\,:\,\, \pm \,\left( {1,3} \right)
- Scrivere l’elenco delle possibili radici razionali trovando {p \over q} che è semplicemente il rapporto tra i fattori del termine costante e leader del termine. Assicurarsi di tenere traccia delle possibili combinazioni.,
Questo è come lo faccio. Prendo ogni numeratore e lo divido per tutti i denominatori. Poi passo al numeratore successivo e divido di nuovo per tutti i denominatori. Continuo a ripetere questo processo fino a quando non ho passato tutti i numeratori. Questo assicura che abbiamo coperto tutte le possibili combinazioni.
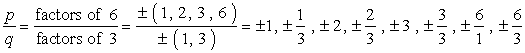
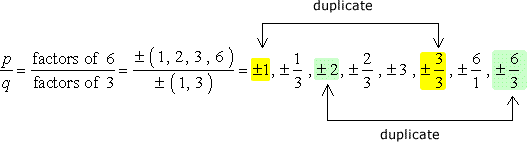
GRANDE attenzione: dopo aver annotato tutte le combinazioni, semplificare le frazioni per eliminare i duplicati.,
Quindi questi sono i numeri senza duplicati che controlleremo come possibili radici. Abbiamo dodici (12) possibili candidati da controllare.
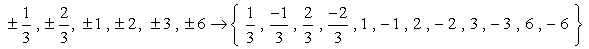
- Ricordate che, se a è una radice del polinomio P\left( x \right), allora P\left( a \right) = 0. Ora, controlliamo ogni numero.,
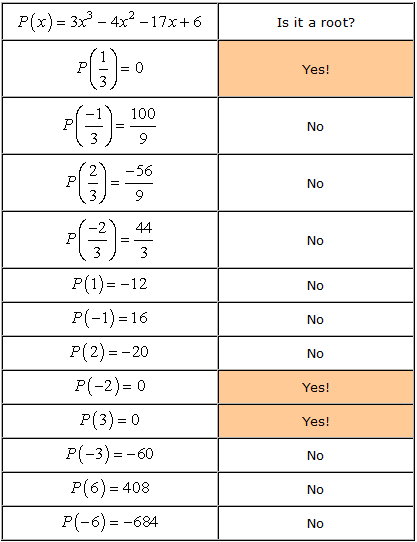
- Therefore, the rational roots of the polynomial
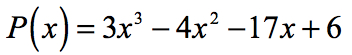
are

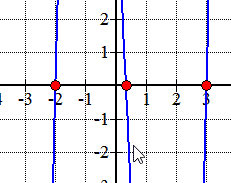
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
Esempio 2: Trova le radici razionali del polinomio sotto usando Rational Roots Test.
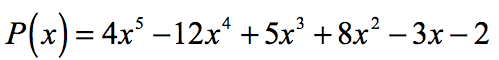
Il termine costante è a0 = -2 e i suoi possibili fattori sono p = ± 1, ± 2. Per il coefficiente principale, abbiamo an = 4 e i suoi fattori sono q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
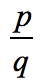
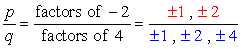
Write down all possible
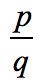
combinations:
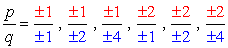
- Simplify each fraction to eliminate duplicates or identical values., Ecco la nostra lista nuova e migliorata!
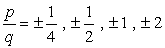
- A causa della considerazione più o meno di ogni numero, avremo otto (8) possibili candidati come radici di questo polinomio.
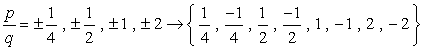
Se si collega ogni valore al polinomio dato e ottiene zero, significa che il numero sostituito è una radice!, Prova questo su carta e dovresti essere convinto che ci sono solo tre valori che soddisfano questa condizione.
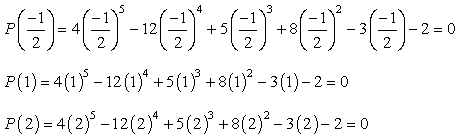
Quindi, le radici razionali di un polinomio
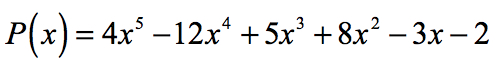
sono
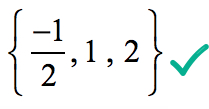
Graficamente, mostra che il polinomio tocca o interseca l’asse x in corrispondenza di quelle radici determinato dalle radici razionali di prova.,