a Rational Roots Test (más néven Rational Zeros tétel) lehetővé teszi számunkra, hogy megtaláljuk a polinom minden lehetséges racionális gyökerét. Tegyük fel, hogy a a polinom gyökere p \ bal (x \ jobb), ami azt jelenti, p\bal( a \ jobb) = 0. Más szavakkal, ha az a-T helyettesítjük a polinomba p\bal( x \jobb), és nullát kapunk, 0, ez azt jelenti, hogy a bemeneti érték a függvény gyökere.
de hogyan találjuk meg a racionális gyökerek lehetséges listáját? Így működik dióhéjban!,
Gombot Ötletek a Racionális Gyökerek Vizsga
Tegyük fel, hogy van egy polinom P\left( x \jobbra) egész együtthatós, valamint egy nem nulla konstans kifejezés:
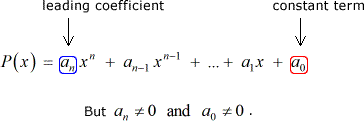
Akkor minden racionális gyökere P\left( x \jobbra) a következő formában:
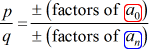
A legjobb módja annak, hogy tanulni ezt a módszert, hogy vessen egy pillantást néhány példát!,
példák arra, hogyan lehet megtalálni a polinom racionális gyökereit a Rational Roots Test segítségével
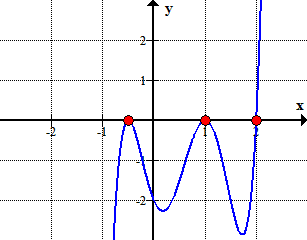
1 példa: keresse meg az alábbi polinom racionális gyökereit a Rational Roots teszt segítségével.
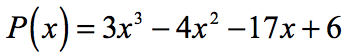
a polinom racionális gyökereinek (más néven racionális nulláknak) megtalálása ugyanaz, mint a racionális x-elfogások megtalálása.
- Kezdje az A0 állandó kifejezés és az An vezető együttható azonosításával.,
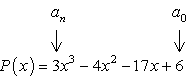
- határozza meg mindegyik pozitív és negatív tényezőjét.
az állandó kifejezés tényezői, {a_0} = 6\,\,:\,\, \pm\, \ left ({1,2,3,6} \ right)
a vezető kifejezés tényezői, {a_n} = 3\,\,:\,\, \pm \,\left( {1,3} \right)
- írja le a lehetséges racionális gyökerek listáját úgy, hogy {p \over q} – T találja meg, ami egyszerűen az állandó kifejezés és a vezető kifejezés tényezőinek aránya. Győződjön meg róla, hogy nyomon követi a lehetséges kombinációkat.,
így csinálom. Minden számlálót beveszek, és elosztom az összes nevezővel. Aztán továbblépek a következő számlálóra, majd ismét megosztom az összes nevezővel. Addig ismételgetem ezt a folyamatot, amíg át nem megyek az összes számlálón. Ez biztosítja, hogy minden lehetséges kombinációt lefedtünk.
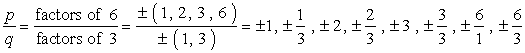
nagy figyelmeztetés: miután leírta az összes kombinációt, egyszerűsítse a frakciókat annak érdekében, hogy megszabaduljon a duplikációktól.,
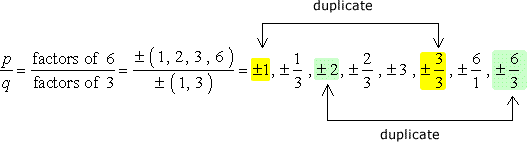
tehát ezek a számok duplikációk nélkül, amelyeket a lehetséges gyökerekként ellenőrizünk. Tizenkét (12) lehetséges jelöltet kell ellenőriznünk.
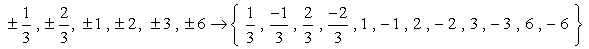
- ne feledje, hogy ha a a polinom gyökere p\bal( x \jobb), akkor P\bal( a \jobb) = 0. Most nézzük meg az egyes számokat.,
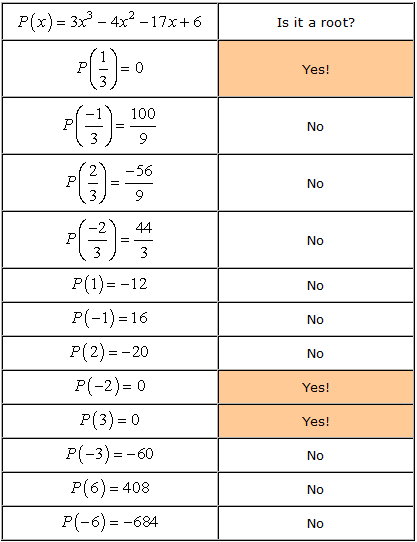
- Therefore, the rational roots of the polynomial
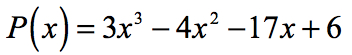
are

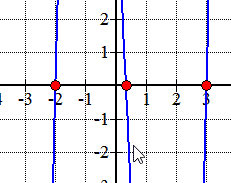
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
2.példa: a lenti polinom racionális gyökereit racionális Roots-teszt segítségével keresse meg.
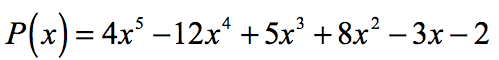
az állandó kifejezés a0 = -2, és lehetséges tényezői p = ± 1, ± 2. A vezető együttható esetében van egy = 4, tényezői pedig q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
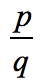
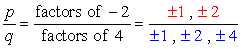
Write down all possible
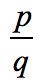
combinations:
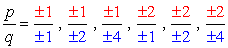
- Simplify each fraction to eliminate duplicates or identical values., Itt az új és továbbfejlesztett listánk!
- az egyes számok plusz vagy mínusz figyelembevétele miatt nyolc (8) lehetséges jelöltünk lesz ennek a polinomnak a gyökerei.
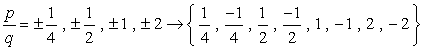
ha minden értéket az adott polinomhoz csatlakoztat, és nullát kap, ez azt jelenti, hogy a helyettesített szám gyökér!, Próbáld ki ezt papíron, és meg kell győződnöd róla, hogy csak három érték felel meg ennek a feltételnek.
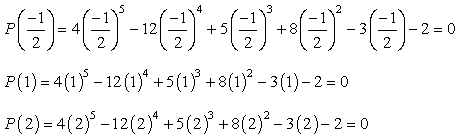
Ezért a racionális gyökerei a polinom
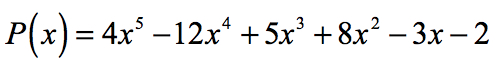
vagy
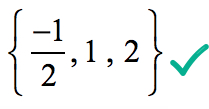
Grafikusan, ez azt mutatja, hogy a polinom érinti vagy metszi az x-tengelyt, azokat a gyökerek által meghatározott ésszerű gyökerek teszt.,