Le Test des racines rationnelles (également connu sous le nom de théorème des zéros rationnels) nous permet de trouver toutes les racines rationnelles possibles d’un polynôme. Supposons que a soit la racine du polynôme P \ left (x \ right), ce qui signifie P\left( a \right) = 0. En d’autres termes, si nous substituons a dans le polynôme P\left( x \right) et obtenons zéro, 0, cela signifie que la valeur d’entrée est une racine de la fonction.
Mais comment trouver la liste possible des racines rationnelles? Voici comment cela fonctionne en un mot!,
les concepts Clés de l’Rationnelle Racines Test
Supposons que nous avons un certain polynôme P\left( x \right) à coefficients entiers et un terme constant non nul:
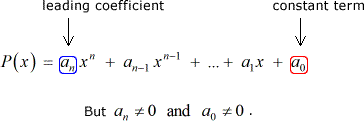
Ensuite, chaque rationnelle racine de P\left( x \right) est de la forme:
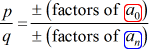
La meilleure façon d’apprendre cette méthode est de prendre un coup d’oeil à quelques exemples!,
exemples de la façon de trouver les racines rationnelles d’un polynôme en utilisant le test de racines rationnelles
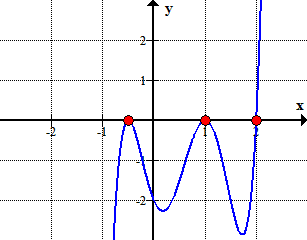
exemple 1: Trouvez les racines rationnelles du polynôme ci-dessous en utilisant le Test de racines rationnelles.
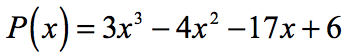
Trouver les racines rationnelles (aussi connu comme rationnelle des zéros) d’un polynôme est la même chose que de trouver le rationnel x intercepte.
- Commencez par identifier le terme constant a0 et le coefficient directeur d’une.,
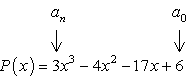
- Déterminer les facteurs positifs et négatifs de chacun.
Facteurs de terme constant, {a_0} = 6\,\,:\,\, \pm \,\left( {1,2,3,6} \right)
Facteurs de mener à terme, {a_n} = 3\,\,:\,\, \pm \,\left( {1,3} \right)
- Écrivez la liste de l’rationnelle possible des racines par trouver {p \over q}, qui est simplement le rapport des facteurs de la constante de terme et conduisant à terme. Assurez-vous de garder les combinaisons possibles.,
Voici comment je le fais. Je prends chaque numérateur et le divise par tous les dénominateurs. Ensuite, je passe au numérateur suivant et je divise à nouveau par tous les dénominateurs. Je continue à répéter ce processus jusqu’à ce que je suis passé par tous les numérateurs. Cela garantit que nous avons couvert toutes les combinaisons possibles.
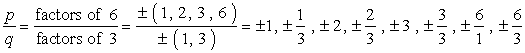
BIG Attention: Après vous écrire toutes les combinaisons, de simplifier les fractions afin d’éliminer les doublons.,
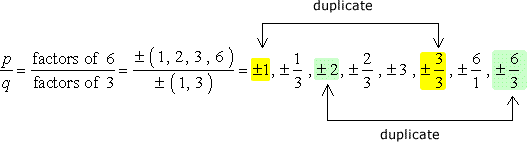
Donc ce sont les chiffres sans les doublons qui nous permettra de vérifier que possible les racines. Nous avons douze (12) candidats possibles à vérifier.
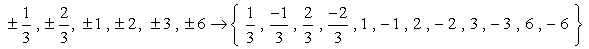
- n’oubliez pas que si a est une racine du polynôme P\left( x \right), alors P\left( a \right) = 0. Maintenant, vérifions chaque numéro.,
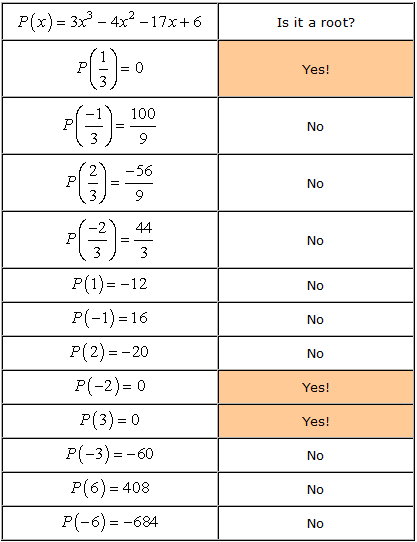
- Therefore, the rational roots of the polynomial
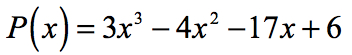
are

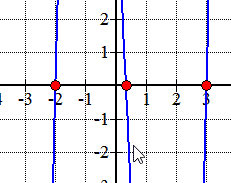
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
Exemple 2: Trouver le rationnel racines du polynôme ci-dessous à l’aide de Racines Rationnelles de Test.
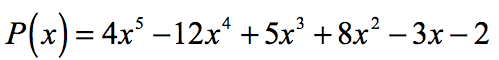
Le terme constant a0 = -2 et ses facteurs sont p = ± 1, ± 2. Pour le coefficient principal, nous avons an = 4 et ses facteurs sont q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
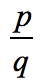
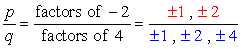
Write down all possible
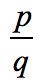
combinations:
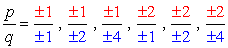
- Simplify each fraction to eliminate duplicates or identical values., Voici notre nouvelle liste améliorée!
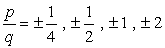
- en Raison de la plus ou moins compte de chaque numéro, nous aurons huit (8) candidats possibles comme les racines de ce polynôme.
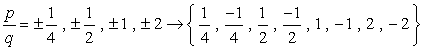
Si vous branchez chaque valeur de la donnée polynôme et devient zéro, cela signifie que le numéro que vous avez substitué est une racine!, Essayez ceci sur papier, et vous devriez être convaincu qu’il n’y a que trois valeurs satisfaisant cette condition.
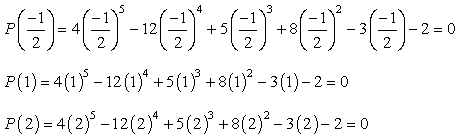
Par conséquent, les racines rationnelles du polynôme