Der Rational Roots Test (auch als Rational Zeros Theorem bekannt) ermöglicht es uns, alle möglichen rationalen Wurzeln eines Polynoms zu finden. Angenommen, a ist die Wurzel des Polynoms P\left( x \right), was P\left (a \right) = 0 bedeutet. Mit anderen Worten, wenn wir a in das Polynom P\left( x \right) ersetzen und Null, 0 erhalten, bedeutet dies, dass der Eingabewert eine Wurzel der Funktion ist.
Aber wie finden wir die mögliche Liste rationaler Wurzeln? So funktioniert es auf den Punkt gebracht!,
Schlüsselideen des rationalen Wurzeltests
Angenommen, wir haben ein Polynom P\left( x \right) mit ganzzahligen Koeffizienten und einem konstanten Term ungleich Null:
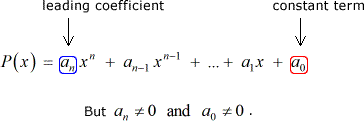
Dann hat jede rationale Wurzel von P\left( x \right) die Form:
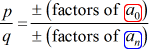
Der beste Weg, diese Methode zu lernen, ist ein Blick auf einige Beispiele!,
Beispiele zum Finden der rationalen Wurzeln eines Polynoms mit dem rationalen Wurzeltest
Beispiel 1: Finden Sie die rationalen Wurzeln des Polynoms unten mit dem rationalen Wurzeltest.
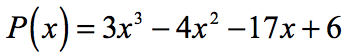
Das Finden der rationalen Wurzeln (auch als rationale Nullen bezeichnet) eines Polynoms ist dasselbe wie das Finden der rationalen x-Intercepts.
- Identifizieren Sie zunächst den konstanten Term a0 und den führenden Koeffizienten an.,
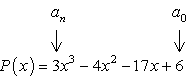
- Bestimmen Sie die positiven und negativen Faktoren der einzelnen.
Faktoren konstanter term, {a_0} = 6\,\,:\,\, \pm \, \ left ({1,2,3,6} \right)
Factors of leading term, {a_n} = 3\,\,:\,\, \pm \, \ left ({1,3} \right)
- Notieren Sie sich die Liste der möglichen rationalen Wurzeln, indem Sie {p \über q} finden, was einfach das Verhältnis der Faktoren des konstanten Terms und des führenden Terms ist. Stellen Sie sicher, dass Sie den Überblick über die möglichen Kombinationen zu halten.,
So mache ich es. Ich nehme jeden Zähler und teile ihn durch alle Nenner. Dann gehe ich zum nächsten Zähler über und dividiere erneut durch alle Nenner. Ich wiederhole diesen Vorgang, bis ich alle Zähler durchlaufen habe. Dies stellt sicher, dass wir alle möglichen Kombinationen abgedeckt haben.
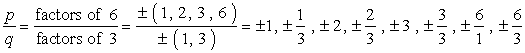
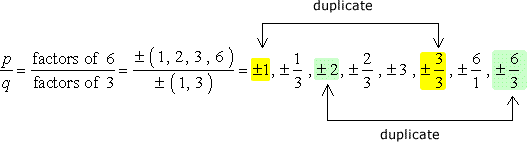
GROßE Vorsicht: Nachdem Sie alle Kombinationen notiert haben, vereinfachen Sie die Brüche, um Duplikate zu entfernen.,
Dies sind also die Zahlen ohne Duplikate, die wir als mögliche Wurzeln überprüfen werden. Wir haben zwölf (12) mögliche Kandidaten zu prüfen.
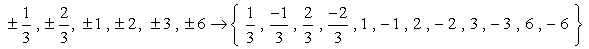
- denken Sie Daran, dass, wenn a eine Wurzel des Polynoms P\left( x \right), dann P\left( a \right) = 0. Lassen Sie uns nun jede Nummer überprüfen.,
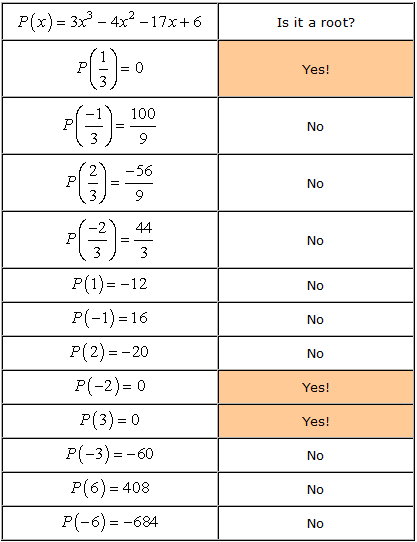
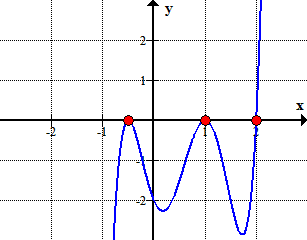
- Therefore, the rational roots of the polynomial
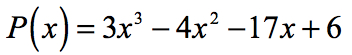
are

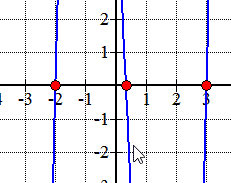
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
Beispiel 2: Finden Sie die rationalen Wurzeln des Polynoms unter Verwendung von Rational Roots Test.
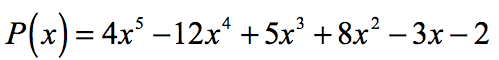
Der Konstante term ist a0 = -2 und seine mögliche Faktoren sind p = ± 1, ± 2. Für den führenden Koeffizienten haben wir an = 4 und seine Faktoren sind q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
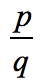
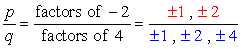
Write down all possible
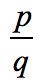
combinations:
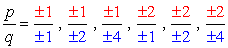
- Simplify each fraction to eliminate duplicates or identical values., Hier ist unsere neue und verbesserte Liste!
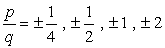
- Aufgrund der Plus-oder Minus-Berücksichtigung jeder Zahl haben wir acht (8) mögliche Kandidaten als Wurzeln dieses Polynoms.
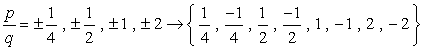
Wenn Sie jeden Wert an das angegebene Polynom anschließen und Null erhalten, bedeutet dies, dass die ersetzte Zahl eine Wurzel ist!, Versuchen Sie dies auf Papier, und Sie sollten überzeugt sein, dass es nur drei Werte gibt, die diese Bedingung erfüllen.
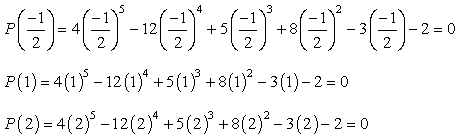
Daher sind die rationalen Wurzeln des Polynoms
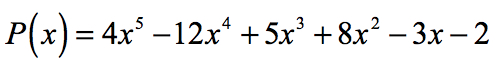
sind
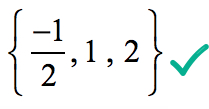
Grafisch zeigt es, dass das Polynom die x-Achse an den durch rational roots test bestimmten Wurzeln berührt oder kreuzt.,