Rational Roots Test (také známý jako Rational Zeros Theorem) nám umožňuje najít všechny možné racionální kořeny polynomu. Předpokládejme, že a je kořen polynomu P \ left (x \ right), což znamená P\left( a \right) = 0. Jinými slovy, pokud nahradíme a do polynomu P \ vlevo (x \ vpravo) a dostaneme nulu, 0, znamená to, že vstupní hodnota je kořenem funkce.
ale jak najdeme možný seznam racionálních kořenů? Zde je návod, jak to funguje v kostce!,
Klíčové Myšlenky Racionální Kořeny Test
Předpokládejme, že máme nějaký polynom P\left( x \right) s celočíselnými koeficienty a nenulovou konstantou termín:
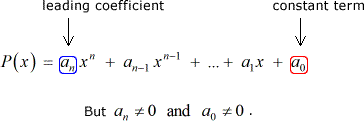
Pak každý racionální kořen P\left( x \right) je ve tvaru:
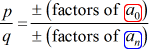
nejlepší způsob, jak se tuto metodu naučit, je podívat se na některé příklady!,
Příklady, Jak Najít Racionální Kořeny Polynomu pomocí Racionální Kořeny Test
Příklad 1: Najděte racionální kořeny polynomu níže pomocí Racionální Kořeny Test.
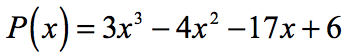
Nalezení racionálních kořenů (také známý jako racionální nuly) polynomu je stejné, jako najít racionální x-zachytí.
- začněte identifikací konstantního výrazu a0 a předního koeficientu an.,
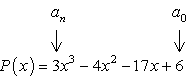
- Určit pozitivní a negativní faktory každého.
Faktory konstantní výraz, {a_0} = 6\,\,:\,\, \pm \,\left( {1,2,3,6} \right)
Faktory vedoucí termín, {a_n} = 3\,\,:\,\, \pm \,\left( {1,3} \right)
- Napsat seznam možné racionální kořeny najít {p \over q}, která je jednoduše poměr faktory konstantní výraz a vedoucí termín. Ujistěte se, že budete sledovat možné kombinace.,
takto to dělám. Vezmu každého čitatele a vydělím ho všemi jmenovateli. Pak přejdu k dalšímu čitateli a znovu vydělím všemi jmenovateli. Opakuji tento proces, dokud jsem neprošel všemi čitateli. Tím je zajištěno, že jsme pokryli všechny možné kombinace.
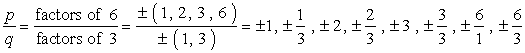
VELKOU Opatrností: Po zapište si všechny kombinace, zjednodušit frakce, ve snaze zbavit se duplikátů.,
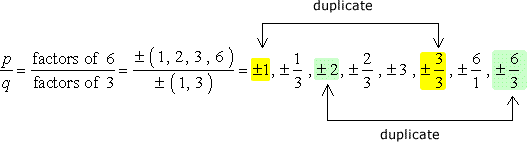
takže se jedná o čísla bez duplikátů, která zkontrolujeme jako možné kořeny. Máme dvanáct (12) možných kandidátů na kontrolu.
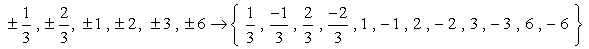
- Pamatujte si, že pokud je kořen polynomu P\left( x \right), pak P\left( a \right) = 0. Teď se podíváme na každé číslo.,
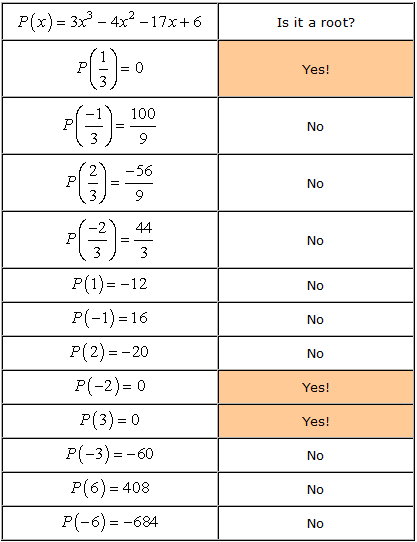
- Therefore, the rational roots of the polynomial
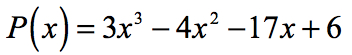
are

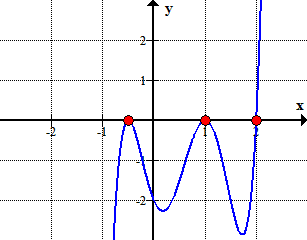
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
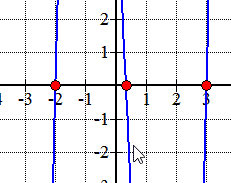
Příklad 2: Najděte racionální kořeny polynomu níže pomocí Racionální Kořeny Test.
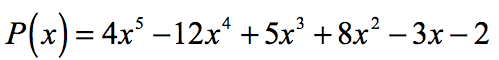
konstantní výraz je a0 = -2 a její možné faktory jsou p = ± 1, ± 2. Pro vedoucí koeficient máme an = 4 a jeho faktory jsou q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
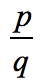
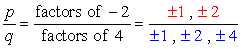
Write down all possible
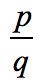
combinations:
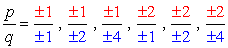
- Simplify each fraction to eliminate duplicates or identical values., Zde je náš nový a vylepšený seznam!
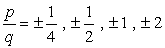
- Vzhledem k plus nebo minus zvážení každé číslo, budeme mít osm (8) možných kandidátů jako kořeny tohoto polynomu.
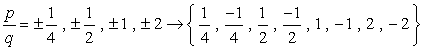
Pokud se připojíte každá hodnota daného polynomu a dostane na nulu, znamená to, že číslo, které jste nahradit je kořen!, Zkuste to na papíře a měli byste být přesvědčeni, že existují pouze tři hodnoty, které tuto podmínku splňují.
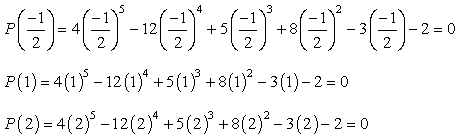
Proto, racionální kořeny polynomu
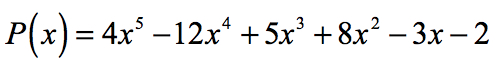
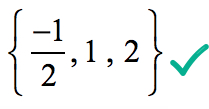
Graficky, to ukazuje, že polynom se dotýká nebo protíná osu x v těchto kořenů určuje racionální kořeny test.,