Rational Roots Test (även känt som Rational Zeros Theorem) gör att vi kan hitta alla möjliga rationella rötter av ett polynom. Antag att A är roten till polynomet p \ left (x \ right) som betyder P\left( a \right) = 0. Med andra ord, om vi ersätter a i polynomet p\left( x \right) och får noll, 0 betyder det att inmatningsvärdet är en rot av funktionen.
men hur hittar vi den möjliga listan över rationella rötter? Så här fungerar det i ett nötskal!,
key Ideas of Rational Roots Test
Antag att vi har några polynom p\left( x \right) med heltalskoefficienter och en nonzero konstant term:
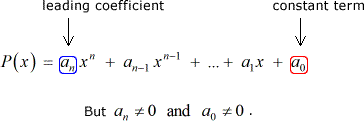
då är varje rationell rot av p\Left( X \right) av formuläret:
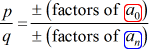
det bästa sättet att lära sig denna metod är att ta en titt på några exempel!,
exempel på hur man hittar de rationella rötterna i ett polynom med hjälp av Rational Roots-testet
exempel 1: Hitta polynomets rationella rötter nedan med hjälp av Rational Roots-testet.
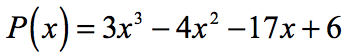
att hitta de rationella rötterna (även kända som rationella nollor) i ett polynom är detsamma som att hitta de rationella X-avlyssningarna.
- börja med att identifiera den konstanta termen A0 och den ledande koefficienten an.,
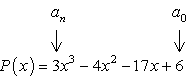
- Bestäm de positiva och negativa faktorerna för varje.
faktorer med konstant term, {a_0} = 6\,\,:\,\, \pm\, \ left ({1,2,3,6} \right)
faktorer av ledande term, {a_n} = 3\,\,:\,\, \pm\, \ left ({1,3} \ right)
- skriv ner listan över möjliga rationella rötter genom att hitta {p \över q} vilket helt enkelt är förhållandet mellan faktorerna för den konstanta termen och ledande termen. Se till att du håller reda på de möjliga kombinationerna.,
Så här gör jag det. Jag tar varje täljare och delar den med alla nämnare. Sedan går jag vidare till nästa täljare och delar igen av alla nämnare. Jag fortsätter att upprepa denna process tills jag har gått igenom alla täljare. Detta säkerställer att vi har täckt alla möjliga kombinationer.
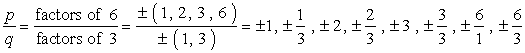
stor försiktighet: när du har skrivit ner alla kombinationer, förenkla fraktionerna för att bli av med dubbletter.,
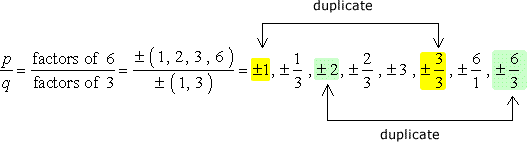
så det här är siffrorna utan dubbletter som vi kommer att kontrollera som möjliga rötter. Vi har tolv (12) möjliga kandidater att kontrollera.
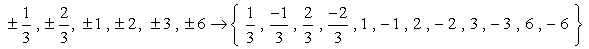
- kom ihåg att om A är en rot av polynomet p\left( x \right), sedan P\left( a \right) = 0. Nu kollar vi varje nummer.,
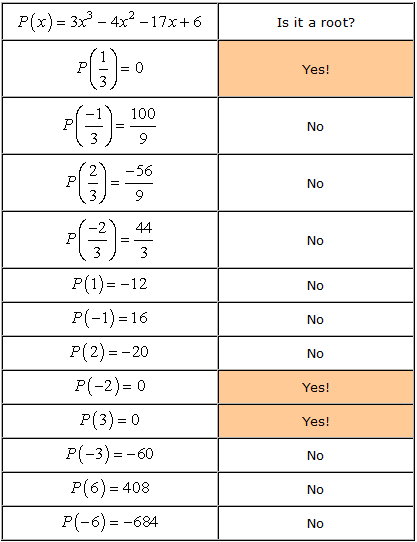
- Therefore, the rational roots of the polynomial
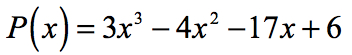
are

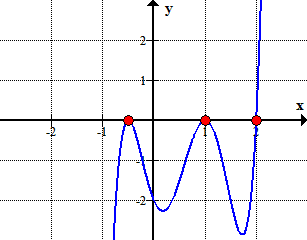
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
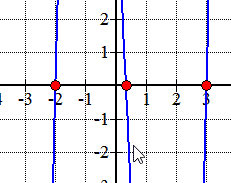
exempel 2: Hitta de rationella rötterna i polynom nedan med hjälp av Rational Roots Test.
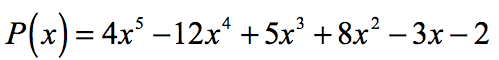
den konstanta termen är A0 = -2 och dess möjliga faktorer är P = ± 1, ± 2. För den ledande koefficienten har vi an = 4 och dess faktorer är q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
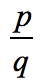
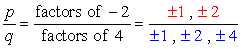
Write down all possible
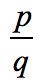
combinations:
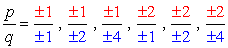
- Simplify each fraction to eliminate duplicates or identical values., Här är vår nya och förbättrade lista!
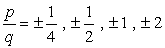
- på grund av plus eller minus övervägande av varje nummer kommer vi att ha åtta (8) möjliga kandidater som rötterna till detta polynom.
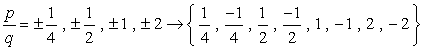
om du ansluter varje värde till det givna polynomet och blir noll betyder det att numret du ersatte är en rot!, Prova detta på papper, och du bör vara övertygad om att det bara finns tre värden som uppfyller detta villkor.
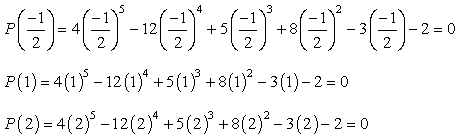
därför rationella rötter polynom
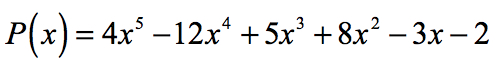
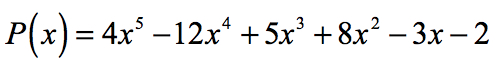
är
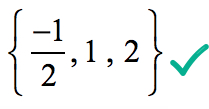
grafiskt visar det att polynomet berör eller korsar x-axeln vid de rötter som bestäms av Rational Roots test.,