The Rational Roots Test (also known as Rational Zeros Theorem) all possible rational roots of a polynomial. Suponha que a é a raiz do polinômio p\esquerda( x \direita) que significa P\esquerda (a \direita) = 0. Em outras palavras, se nós substituirmos a no polinômio p\esquerda (x \direita) e obter zero, 0, significa que o valor de entrada é uma raiz da função.mas como encontramos a possível Lista de raízes racionais? É assim que funciona em poucas palavras!,
Ideias-Chave de Raízes Racionais de Teste
Suponhamos que temos algum polinˆ omio P\left( x \right) com coeficientes inteiros e um termo constante diferente de zero:
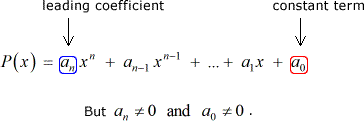
em Seguida, a cada racional raiz de P\left( x \right) é da forma:
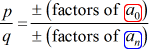
A melhor maneira de aprender este método é dar uma olhada em alguns exemplos!,
Examples of How to Find the Rational Roots of a Polynomial using the Rational Roots Test
Example 1: Find the rational roots of the polynomial below using the Rational Roots Test.
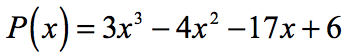
Encontrar o racional raízes (também conhecido como racional zeros) de um polinômio é o mesmo que encontrar o racional x intercepta.
- comece por identificar o termo constante a0 e o coeficiente inicial an.,
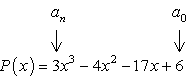
- Determinar os pontos positivos e negativos de cada um.
Fatores de termo constante, {a_0} = 6\,\,:\,\, \pm \,\left( {1,2,3,6} \right)
Fatores de líder a prazo, {a_n} = 3\,\,:\,\, \pm \,\left( {1,3} \right)
- Escreva a lista dos possíveis raízes racionais, encontrando {p \over q}, que é simplesmente a relação dos fatores do termo constante e levando a termo. Certifique-se de manter o controle das combinações possíveis.,é assim que eu faço. Pego em cada numerador e divido-o por todos os denominadores. Depois passo para o numerador seguinte e divido novamente por todos os denominadores. Continuo a repetir este processo até ter passado por todos os numeradores. Isto garante que temos coberto todas as combinações possíveis.
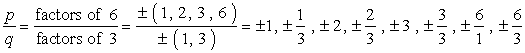
GRANDE Cuidado: Depois de escrever todas as combinações, simplifique as frações, a fim de se livrar de duplicatas.,
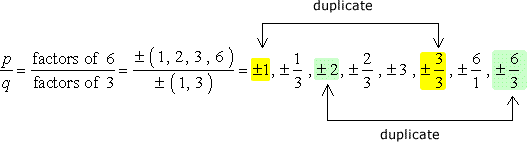
Então, estes são os números sem duplicatas que iremos verificar possível raízes. Temos doze (12) candidatos possíveis para verificar.
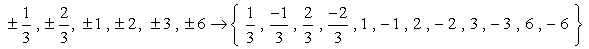
- Lembre-se que se a é uma raiz do polinômio P\left( x \right), então P\left( um \right) = 0. Agora, vamos verificar cada número.,
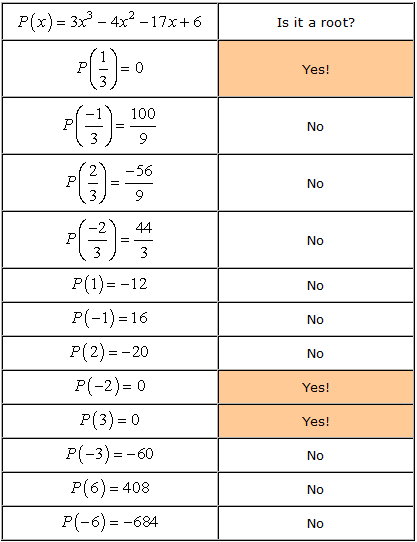
- Therefore, the rational roots of the polynomial
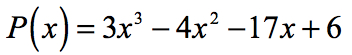
are

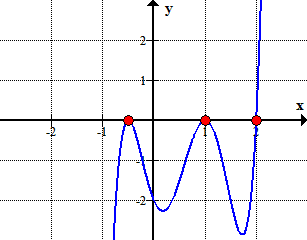
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
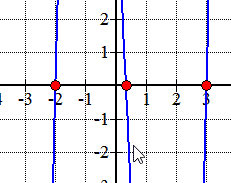
Exemplo 2: Encontrar o racional raízes do polinômio abaixo usando o Rational Raízes de Teste.
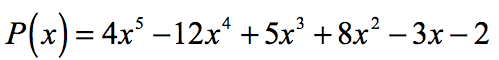
O termo constante é a0 = -2 e seus possíveis fatores de são p = ± 1, ± 2. Para o coeficiente líder, temos an = 4 e seus fatores são q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
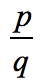
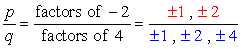
Write down all possible
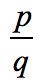
combinations:
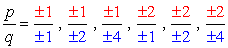
- Simplify each fraction to eliminate duplicates or identical values., Aqui está a nossa nova e melhorada lista!
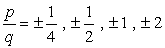
- Devido à mais ou menos a consideração de cada número, teremos oito (8) candidatos possíveis, como as raízes deste polinômio.
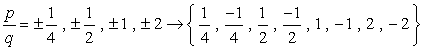
Se você conectar em cada valor para o dado polinômio e fica zero, que significa o número que você substituído é uma raiz!, Tente isso no papel, e você deve estar convencido de que existem apenas três valores que satisfazem esta condição.
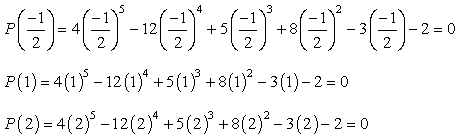
Portanto, o racional raízes do polinômio
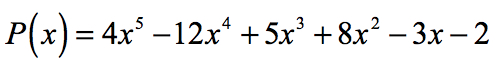
são
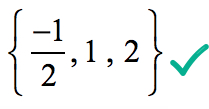
Graficamente, isso mostra que o polinˆ omio toca ou cruza o eixo x em raízes determinado pelo racional raízes de teste.,