op deze pagina schetsen we de drie principes die u moet begrijpen met betrekking tot serie circuits:
- stroom: de hoeveelheid stroom is gelijk door elk onderdeel in een serie circuit.
- weerstand: de totale weerstand van een seriekring is gelijk aan de som van de afzonderlijke weerstanden.
- spanning: de voedingsspanning in een seriekring is gelijk aan de som van de individuele spanningsdalingen.,
laten we eens kijken naar enkele voorbeelden van serie circuits die deze principes demonstreren.
we beginnen met een seriecircuit bestaande uit drie weerstanden en een enkele batterij:

het eerste principe dat we begrijpen over seriecircuits is als volgt:
de hoeveelheid stroom in een seriecircuit is gelijk door elk onderdeel in het circuit.
Dit komt omdat er slechts één pad is voor stroom in een seriecircuit., Omdat elektrische lading door geleiders stroomt als knikkers in een buis, moet de stroomsnelheid (marmersnelheid) op elk punt in het circuit (buis) op elk specifiek punt in de tijd gelijk zijn.
met behulp van de wet van Ohm in Seriecircuits
uit de manier waarop de 9-volt batterij is gerangschikt, kunnen we zien dat de stroom in dit circuit met de klok mee zal stromen, van punt 1 naar 2 naar 3 naar 4 en terug naar 1. We hebben echter één spanningsbron en drie weerstanden. Hoe gebruiken we Ohm ‘ s wet hier?,
een belangrijk voorbehoud bij de wet van Ohm is dat alle grootheden (spanning, stroom, weerstand en vermogen) met elkaar in verband moeten staan in termen van dezelfde twee punten in een circuit. We kunnen dit concept in actie zien in het enkele weerstand circuit voorbeeld hieronder.,
met Behulp van de Wet van Ohm in een Eenvoudige, Enkele Weerstand Circuit
Met een single-batterij, één weerstand circuit, kunnen we eenvoudig berekenen welke hoeveelheid, omdat ze allemaal op dezelfde twee punten in het circuit:


Sinds de punten 1 en 2 zijn met elkaar verbonden met de draad van te verwaarlozen weerstand, net als de punten 3 en 4, kunnen we zeggen dat punt 1 is elektrisch gemeenschappelijk punt 2 en punt 3 is het elektrisch gemeenschappelijk punt 4., Omdat we weten dat we 9 volt elektromotorische kracht hebben tussen de punten 1 en 4 (direct over de batterij), en omdat punt 2 gemeenschappelijk is met punt 1 en punt 3 gemeenschappelijk met punt 4, moeten we ook 9 volt hebben tussen de punten 2 en 3 (direct over de weerstand).
daarom kunnen we Ohm ‘ s wet (I = E/R) toepassen op de stroom door de weerstand, omdat we de spanning (E) over de weerstand en de weerstand (R) van die weerstand kennen. Alle termen (E, I, R) zijn van toepassing op dezelfde twee punten in het circuit, op dezelfde weerstand, zodat we de Ohm ‘ s Law formule zonder voorbehoud kunnen gebruiken.,
door gebruik te maken van de wet van Ohm in Circuits met meerdere weerstanden
In circuits die meer dan één weerstand bevatten, moeten we voorzichtig zijn in hoe we de wet van Ohm toepassen. In het drieweerstands voorbeeld circuit hieronder, weten we dat we 9 volt tussen de punten 1 en 4, dat is de hoeveelheid elektromotorische kracht die de stroom door de serie combinatie van R1, R2 en R3. We kunnen echter niet de waarde van 9 volt nemen en deze delen door 3k, 10k of 5k Ω om een stroomwaarde te vinden, omdat we niet weten hoeveel spanning er over een van deze weerstanden afzonderlijk is.,

het cijfer van 9 volt is een totale hoeveelheid voor het hele circuit, terwijl de cijfers van 3k, 10k en 5k Ω individuele hoeveelheden voor individuele weerstanden zijn. Als we een cijfer voor de totale spanning in een Wetvergelijking van Ohm zouden stoppen met een cijfer voor de individuele weerstand, zou het resultaat niet nauwkeurig betrekking hebben op enige hoeveelheid in het echte circuit.,
voor R1 zal de wet van Ohm de hoeveelheid spanning over R1 relateren aan de stroom door R1, gegeven de weerstand van R1, 3kΩ:

maar omdat we de spanning over R1 niet kennen (alleen de totale spanning die door de batterij wordt geleverd over de combinatie van de drieweerstands-serie) en we de stroom niet kennen door R1, kunnen we geen berekeningen maken met beide formules. Hetzelfde geldt voor R2 en R3: we kunnen de Wetvergelijkingen van Ohm alleen dan toepassen als alle termen representatief zijn voor hun respectievelijke grootheden tussen dezelfde twee punten in het circuit.,
dus wat kunnen we doen? We kennen de spanning van de bron (9 volt) toegepast over de serie combinatie van R1, R2, en R3, en we kennen de weerstand van elke weerstand, maar omdat die hoeveelheden niet in dezelfde context, kunnen we niet Ohm ‘ s Wet gebruiken om de stroom van de schakeling te bepalen. Wisten we maar wat de totale weerstand voor het circuit was: dan konden we de totale stroom berekenen met ons cijfer voor de totale spanning (I=E/R).,
het combineren van meerdere weerstanden tot een equivalente totale weerstand
brengt ons bij het tweede principe van seriecircuits:
de totale weerstand van een seriecircuit is gelijk aan de som van de individuele weerstanden.
Dit zou intuïtief logisch moeten zijn: hoe meer weerstanden in serie waar de stroom doorheen moet stromen, hoe moeilijker het zal zijn voor de stroom om te stromen.,
in het voorbeeld probleem, we hadden een 3 kΩ, 10 kΩ, en 5 kω weerstanden in serie, wat ons een totale weerstand van 18 kΩ geeft:

in wezen hebben we de equivalente weerstand van R1, R2 en R3 gecombineerd berekend.,oltages gebruikmakend van Ohm ‘ s wet
wetende dat de stroom gelijk is door alle componenten van een serie circuit (en we hebben net de stroom door de batterij bepaald), kunnen we teruggaan naar ons oorspronkelijke circuit schema en noteer de stroom door elke component:
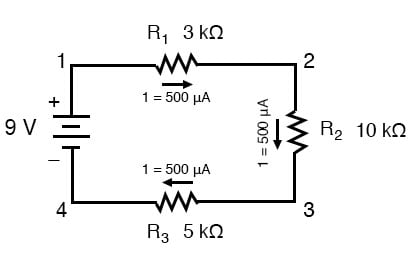
nu we de hoeveelheid stroom door elke weerstand weten, kunnen we Ohm ’s Wet gebruiken om de spanningsval over elke één te bepalen (Ohm’ s toepassen wet in zijn juiste context):

merk op dat de spanning over elke weerstand daalt en hoe de som van de spanning daalt (1.,5 + 5 + 2.5) is gelijk aan de batterij (voeding) spanning: 9 volt.
Dit is het derde principe van seriecircuits:
De voedingsspanning in een seriecircuit is gelijk aan de som van de individuele spanningsdalingen.
het analyseren van eenvoudige Series Circuits met de” Table Method “en Ohm’ s Law
echter, de methode die we net hebben gebruikt om dit eenvoudige serie circuit te analyseren kan worden gestroomlijnd voor een beter begrip., Door een tabel te gebruiken om alle spanningen, stromen en weerstand in het circuit weer te geven, wordt het heel gemakkelijk om te zien welke van deze grootheden correct gerelateerd kunnen worden in de Wetvergelijking van Ohm:

de regel met een dergelijke tabel is om de wet van Ohm alleen toe te passen op de waarden binnen elke verticale kolom. Bijvoorbeeld, ER1 alleen met IR1 EN R1; ER2 alleen met IR2 en R2; enz., U begint uw analyse door de elementen van de tabel in te vullen die u vanaf het begin zijn gegeven:

zoals u kunt zien aan de rangschikking van de gegevens, kunnen we de 9 volt van ET (totale spanning) niet toepassen op een van de weerstanden (R1, R2 of R3) in de Wetformule van Ohm omdat ze in verschillende kolommen staan. De 9 volt batterijspanning wordt niet direct toegepast over R1, R2 of R3. We kunnen echter onze “regels” van seriecircuits gebruiken om lege plekken op een horizontale rij in te vullen.,t van 500 µA:

dan, wetende dat de stroom gelijk wordt gedeeld door alle componenten van een seriecircuit (een andere “regel” van seriecircuits), kunnen we de stromen voor elke weerstand invullen van de zojuist berekende stroom:

ten slotte kunnen we de wet van Ohm gebruiken om de spanningsval over elke weerstand te bepalen, één kolom tegelijk:

berekeningen verifiëren met computer analysis (spice)
voor de lol, kunnen we een computer gebruiken om hetzelfde circuit automatisch te analyseren., Het zal een goede manier zijn om onze berekeningen te verifiëren en ook meer vertrouwd te raken met computeranalyse. Eerst moeten we het circuit naar de computer beschrijven in een formaat dat herkenbaar is aan de software.
het SPICE programma dat we zullen gebruiken vereist dat alle elektrisch unieke punten in een circuit genummerd zijn, en component plaatsing wordt begrepen door welke van die genummerde punten, of “knooppunten,” ze delen. Voor de duidelijkheid heb ik de vier hoeken van ons voorbeeldcircuit 1 tot en met 4 genummerd., SPICE eist echter dat er ergens een knooppunt nul is in het circuit, dus Ik zal het circuit opnieuw tekenen en het nummering schema iets veranderen:

alles wat ik hier heb gedaan is de linkerbenummerhoek van het circuit 0 in plaats van 4. Nu kan ik een aantal regels tekst invoeren in een computerbestand dat het circuit beschrijft in termen die SPICE zal begrijpen, compleet met een paar extra regels code die het programma leiden om spanning en stroomgegevens weer te geven voor ons kijkplezier., Dit computerbestand is bekend als de netlist in SPICE terminologie:
series circuit v1 1 0 r1 1 2 3k r2 2 3 10k r3 3 0 5k .dc v1 9 9 1 .print dc v(1,2) v(2,3) v(3,0) .end
Nu, alles wat ik moet doen is het uitvoeren van de SPICE-programma voor het verwerken van de netlijst en de output van de resultaten:
| v1 | v(1,2) | v(2,3) | v(3) | i(v1) |
|---|---|---|---|---|
| 9.000 E+00 | 1.500 E+00 | 5.000 E+00 | 2.500 E+00 | -5.,000E-04 |
deze print geeft aan dat de batterijspanning 9 volt is en dat de spanning over R1, R2 en R3 respectievelijk 1,5 volt, 5 volt en 2,5 volt bedraagt. Spanningsdalingen over een component in SPICE worden verwezen door de knooppuntnummers waar de component tussen ligt, dus v (1,2) verwijst naar de spanning tussen knooppunten 1 en 2 in het circuit, die de punten zijn waartussen R1 zich bevindt.,
De volgorde van knooppuntnummers is belangrijk: wanneer SPICE een cijfer voor v(1,2) geeft, beschouwt het de polariteit op dezelfde manier als wanneer we een voltmeter met de rode testsnoer op knooppunt 1 en de zwarte testsnoer op knooppunt 2 vasthouden. We hebben ook een display met stroom (zij het met een negatieve waarde) bij 0,5 milliamp of 500 microamps. Dus onze wiskundige analyse is bevestigd door de computer. Dit cijfer verschijnt als een negatief getal in de SPICE analyse, als gevolg van een eigenaardigheid in de manier waarop SPICE omgaat met de huidige berekeningen.,
samengevat wordt een seriekring gedefinieerd als het hebben van slechts één pad waardoor stroom kan stromen. Uit deze definitie volgen drie regels van seriecircuits: alle componenten delen dezelfde stroom; weerstanden voegen toe aan een grotere totale weerstand; en spanningsdalingen voegen toe aan een grotere totale spanning. Al deze regels vinden hun oorsprong in de definitie van een seriecircuit. Als je die definitie volledig begrijpt, dan zijn de regels niets meer dan voetnoten bij de definitie.
recensie:
- componenten in een seriecircuit delen dezelfde stroom: ITotal = I1 = I2 = . . ., In
- is de totale weerstand in een seriecircuit gelijk aan de som van de individuele weerstanden: RTotal = R1 + R2 + . . . Rn
- totale spanning in een seriekring is gelijk aan de som van de individuele spanningsdalingen ETotal = E1 + E2 + . . . Nl
Probeer onze Ohm ‘ s Law Calculator in onze Tools sectie.
gerelateerde werkbladen:
- serie DC Circuits Oefenwerkblad met antwoorden werkblad
- algebraïsche vergelijking manipulatie voor elektrische Circuits werkblad