een ding dat we veel zullen doen met de algoritmen in deze reeks is graph traversal. Wat betekent dit precies?
in principe is het idee dat we de grafiek van het ene punt naar het andere zullen verplaatsen en de eigenschappen van hun onderling verbonden relaties zullen ontdekken.
twee van de meest gebruikte algoritmen die we veel zullen gebruiken zijn: Depth-First Search (DFS) en Breadth-First Search (BFS).,
hoewel beide algoritmen ons in staat stellen grafieken te doorlopen, verschillen ze op verschillende manieren. Laten we beginnen met DFS.
DFS maakt gebruik van de” go deep, head first ” filosofie in zijn implementatie. Het idee is dat we vanaf een beginpunt (of plaats) een pad volgen tot we het einde bereiken en als we onze bestemming niet bereiken, dan komen we terug en gaan we een ander pad af.
laten we een voorbeeld bekijken., Stel we hebben een gerichte graaf die er als volgt uitziet:

Nu het idee is dat we beginnen bij vertex s en we zijn gevraagd om te vinden van top t. Met DFS, we gaan samen een pad, ga helemaal naar het einde en als we het niet vinden t, dan gaan we een ander pad af., Hier is het proces:

dus hier gaan we het pad (p1) van het eerste naastgelegen Vertex af en we zien dat het niet het einde is omdat het een pad naar een ander Vertex heeft., Dus we gaan dat pad in:
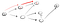
Dit is duidelijk niet de top t dus we moeten teruggaan omdat we een doodlopende weg hebben bereikt. Aangezien het vorige knooppunt geen buren meer heeft, gaan we terug naar s., Vanuit s gaan we naar het tweede naastgelegen knooppunt:
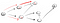
op het pad (P2) worden we geconfronteerd met drie buren., Sinds de eerste heeft al zijn bezocht, hebben we naar beneden te gaan de tweede:
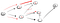
Nu, eenmaal weer hebben we op een dood spoor dat is niet de vertex t dus we moeten terug., Omdat er een andere buurman die nog niet is bezocht, we gaan die naburige pad en op het laatst vonden we het de vertex t:

Dit is hoe DFS werkt. Ga een pad af en ga door tot je de bestemming of een doodlopende weg hebt bereikt. Als het de bestemming is, ben je klaar. Als dat niet zo is, ga dan terug en volg een ander pad totdat je alle opties binnen dat pad hebt uitgeput.,
we kunnen zien dat we dezelfde procedure volgen op elk hoekpunt dat we bezoeken:
doe een DFS voor elke buur van het hoekpunt
aangezien dit inhoudt dat we dezelfde procedure bij elke stap moeten doen, vertelt iets ons dat we recursie moeten gebruiken om dit algoritme te implementeren.
Hier is de code in JavaScript:
opmerking: met dit specifieke DFS-algoritme kunnen we bepalen of het mogelijk is om van de ene plaats naar de andere te gaan., DFS kan op verschillende manieren worden gebruikt en er kunnen subtiele veranderingen zijn in het bovenstaande algoritme. Het algemene concept blijft echter hetzelfde.
analyse van DFS
laten we nu dit algoritme analyseren. Omdat we door elke buur van het knooppunt gaan en we de bezochte negeren, hebben we een runtime van O(V + E).
een korte uitleg van wat V + E precies betekent:
V vertegenwoordigt het totale aantal hoekpunten. E staat voor het totale aantal randen. Elke top heeft een aantal randen.,
hoewel het lijkt dat men kan worden geleid om te geloven dat het V•E is in plaats van V + E, laten we eens nadenken over wat V•E precies betekent.wil iets V * E zijn, dan betekent dit dat we voor elk hoekpunt naar alle randen in de grafiek moeten kijken, ongeacht of die randen verbonden zijn met dat specifieke hoekpunt.
terwijl, aan de andere kant, V + E betekent dat Voor elk hoekpunt, we alleen kijken naar het aantal randen die betrekking hebben op dat hoekpunt. Herinneren van de vorige post, dat de ruimte die we nemen voor de adjacency lijst is O(V + E)., Elk vertex heeft een aantal randen en in het ergste geval, als we DFS zouden draaien op elk vertex, zouden we O(V) werk hebben gedaan samen met het verkennen van alle randen van de hoekpunten, dat is O(E). Als we eenmaal hebben gekeken naar alle v aantal hoekpunten, zouden we ook hebben gekeken naar een totaal van e randen. Daarom is het nu V + E.
, aangezien DFS recursie gebruikt op elk hoekpunt, betekent dit dat een stack wordt gebruikt (daarom wordt het een stack overflow fout genoemd wanneer je een oneindige recursieve aanroep tegenkomt). Daarom is de complexiteit van de ruimte O (V).,
laten we nu eens kijken hoe breedte-eerste zoekopdracht verschilt.
Breadth-First Search
Breadth-First Search (BFS) volgt de “go wide, bird ‘ s eye-view” filosofie. Wat dat in principe betekent is dat in plaats van helemaal naar beneden te gaan tot het einde, BFS beweegt naar zijn bestemming een buur per keer., Laten we eens kijken wat dat betekent:

dus in plaats van gewoon helemaal naar beneden te gaan, zou bfs eerst alle buren van s bezoeken en dan de buren van die buren bezoeken enzovoort totdat het t bereikt.,fd17d”>


See how different DFS and BFS behave?, Hoewel ik graag denk dat DFS graag het hoofd op gaat, kijkt BFS graag langzaam en observeert alles stap voor stap.
een vraag die ons opvalt zou moeten zijn: “hoe weten we welke buren we het eerst moeten bezoeken van de buren van s?”
Nou, we kunnen gebruik maken van een wachtrij first-in-first-out (FIFO) eigenschap waar we pop de eerste hoekpunt van de wachtrij, Voeg zijn niet bezochte buren aan de wachtrij, en dan doorgaan met dit proces totdat de wachtrij is ofwel leeg of het hoekpunt dat we toevoegen aan het is het hoekpunt waar we naar op zoek zijn.,
laten we nu eens kijken naar de code in JavaScript:
analyse van BFS
Het kan lijken alsof BFS langzamer is. Maar als je goed kijkt naar de visualisaties van zowel BFS als DFS, zul je zien dat ze eigenlijk dezelfde runtime hebben.
de wachtrij zorgt ervoor dat ten hoogste elke hoekpunt zal worden verwerkt totdat het de bestemming bereikt. Dus dat betekent in het slechtste geval, dat BFS ook naar alle hoekpunten en alle randen zal kijken.,
hoewel BFS langzamer lijkt, wordt het eigenlijk sneller geacht omdat als we ze op grotere grafieken implementeren, je zult merken dat DFS veel tijd verspilt door lange paden af te leggen die uiteindelijk verkeerd zijn. In feite wordt BFS vaak gebruikt in algoritmen om het kortste pad van de ene top naar de andere te bepalen, maar we zullen die later bespreken.
dus omdat de runtimes hetzelfde zijn, heeft BFS een runtime van O(V + E) en door het gebruik van een wachtrij die maximaal V hoekpunten kan bevatten, heeft het een ruimtecomplexiteit van O(V).,
analogieën om te stoppen met
Ik wil je laten met andere manieren die ik me persoonlijk inbeeld hoe DFS en BFS werken in de hoop dat het je ook zal helpen herinneren.
wanneer ik aan DFS denk, denk ik graag aan iets dat het juiste pad vindt door tegen veel doodlopende wegen aan te lopen. Meestal zou dit zijn als een muis die door een doolhof gaat om voedsel te zoeken.,zou proberen een pad, dat vinden de weg is een doodlopende weg, kantel vervolgens een ander pad en herhaal dit proces totdat hij zijn doel bereikt:

En dit is wat een vereenvoudigde versie van het proces er als volgt uit:

Nu voor BFS, Ik heb altijd gedacht als een rimpeling.,div>

net als hoe BFS begint bij de bron en bezoeken de bron van de buren en vervolgens gaat meer naar buiten door een bezoek aan hun buren en zo op:

Overzicht
- Depth-First Search (DFS) en de Breedte-First Search (BFS) worden beide gebruikt voor het doorsnijden van grafieken.,
- DFS laadt een pad op totdat het dat pad heeft uitgeput om zijn doel te vinden, terwijl BFS door naburige hoekpunten rimpelt om zijn doel te vinden.
- DFS gebruikt een stack terwijl BFS een wachtrij gebruikt.
- zowel DFS als BFS hebben een runtime van O (V + E) en een ruimtecomplexiteit van O(V).
- beide algoritmen hebben verschillende filosofieën, maar hebben evenveel belang in hoe we grafieken doorkruisen.