Madame Lelica

Inleiding

welkom in de wereld van waarschijnlijkheid in Data Science! Laat ik beginnen met een intuïtief voorbeeld.

stel dat u docent bent aan een universiteit. Na het controleren van opdrachten voor een week, heb je alle studenten beoordeeld. Je gaf deze gegradueerde papers aan een data entry man op de universiteit en vertelde hem om een spreadsheet te maken met de cijfers van alle studenten., Maar de man slaat alleen de cijfers op en niet de overeenkomstige studenten.

hij maakte nog een blunder, hij miste een paar inzendingen in een haast en we hebben geen idee wiens cijfers ontbreken. Laten we een manier vinden om dit op te lossen.

een manier is dat u de cijfers visualiseert en ziet of u een trend in de gegevens kunt vinden.

de grafiek die u hebt plot wordt de frequentieverdeling van de gegevens genoemd. Je ziet dat er een gladde kromme-achtige structuur is die onze gegevens definieert,maar zie je een anomalie?, We hebben een abnormaal lage frequentie bij een bepaald scorebereik. Dus de beste gok zou zijn om ontbrekende waarden die de deuk in de verdeling te verwijderen.

Dit is hoe je zou proberen om een real-life probleem op te lossen met behulp van data-analyse. Voor elke Data Scientist, een student of een beoefenaar, distributie is een must know concept. Het biedt de basis voor analytics en inferentiële statistieken.

hoewel het concept van waarschijnlijkheid ons de wiskundige berekeningen geeft, helpen distributies ons om daadwerkelijk te visualiseren wat er onder gebeurt.,

in dit artikel heb ik een aantal belangrijke kansverdelingen behandeld die zowel helder als Uitgebreid worden uitgelegd.

Opmerking: Dit artikel gaat ervan uit dat u een basiskennis van waarschijnlijkheid hebt. Zo niet, dan kunt u deze kansverdelingen verwijzen.,

inhoudsopgave

1. gemeenschappelijke gegevenstypen
2. soorten distributies
   1. Bernoulli distributie
   2. uniforme distributie
   3. binomiale distributie
   4. normale distributie
   5. Poisson distributie
   6. exponentiële distributie
3. relaties tussen de distributies
4. Test uw kennis!

gemeenschappelijke gegevenstypen

voordat we verder gaan met de uitleg van distributies, laten we eens kijken wat voor soort gegevens we kunnen tegenkomen. De gegevens kunnen discreet of continu zijn.,

Discrete gegevens, zoals de naam al doet vermoeden, kunnen alleen gespecificeerde waarden aannemen. Als je bijvoorbeeld een Dobbelsteen rolt, zijn de mogelijke uitkomsten 1, 2, 3, 4, 5 of 6 en niet 1,5 of 2,45.

continue gegevens kunnen elke waarde binnen een bepaald bereik aannemen. Het bereik kan eindig of oneindig zijn. Bijvoorbeeld, het gewicht of de lengte van een meisje, de lengte van de weg. Het gewicht van een meisje kan elke waarde van 54 kg, of 54.5 kg, of 54.5436 kg.

laten we nu beginnen met de soorten distributies.,

soorten distributies

Bernoulli distributie

laten we beginnen met de makkelijkste distributie die Bernoulli distributie is. Het is eigenlijk makkelijker te begrijpen dan het klinkt!

alle cricket junkies die er zijn! Aan het begin van een cricketwedstrijd, hoe beslis je wie er gaat slaan of bal? Een worp! Het hangt er allemaal van af of je wint of verliest, toch? Laten we zeggen dat als de worp resulteert in een hoofd, je wint. Anders verlies je. Er is geen midway.

een verdeling van Bernoulli heeft slechts twee mogelijke uitkomsten, namelijk 1 (succes) en 0 (falen), en één enkele proef., Dus de willekeurige variabele X die een Bernoulli distributie heeft kan waarde 1 nemen met de kans op succes, zeg p, en de waarde 0 met de kans op mislukking, zeg q of 1-p.

Hier staat het voorkomen van een kop voor succes, en het voorkomen van een staart voor mislukking.kans op het krijgen van een kop = 0,5 = kans op het krijgen van een staart omdat er slechts twee mogelijke uitkomsten zijn.

De kansmassafunctie wordt gegeven door: px (1-p)1-x waarbij x € (0, 1).,
Het kan ook geschreven worden als

de kans op succes en mislukking hoeft niet even waarschijnlijk te zijn, zoals het resultaat van een gevecht tussen Me en Undertaker. Hij zal zeker winnen. Dus in dit geval is de kans op mijn succes 0,15 terwijl mijn mislukking 0,85

is hier, is de kans op succes(p) niet hetzelfde als de kans op mislukking. Dus, de grafiek hieronder toont de Bernoulli verdeling van onze strijd.

Hier is de kans op succes = 0,15 en de kans op falen = 0,85., De verwachte waarde is precies wat het klinkt. Als ik je sla, verwacht ik misschien dat je me terug Slaat. In principe is de verwachte waarde van een distributie Het gemiddelde van de distributie., De verwachte waarde van een stochastische variabele X uit een Bernoulli verdeling is als volgt vastgesteld:

E(X) = 1*p + 0*(1-p) = p

De variantie van een stochastische variabele uit een bernoulli verdeling is:

V(X) = E(X2) – 2 = p – p2 = p(1-p)

Er zijn veel voorbeelden van Bernoulli verdeling zoals de vraag of het gaat morgen regenen of niet waar regen geeft succes en geen regen betekent mislukking en het Winnen van (succes) of verliezen (niet aan) het spel.

uniforme verdeling

wanneer u een eerlijke Dobbelsteen rolt, zijn de uitkomsten 1 tot 6., De kansen op het krijgen van deze resultaten zijn even waarschijnlijk en dat is de basis van een uniforme verdeling. In tegenstelling tot Bernoulli distributie, zijn alle n aantal mogelijke uitkomsten van een uniforme verdeling even waarschijnlijk.

een variabele X wordt gelijkmatig verdeeld als de dichtheidsfunctie:

de grafiek van een uniforme distributiecurve lijkt op

u kunt zien dat de vorm van de uniforme distributiecurve rechthoekig is, de reden waarom uniforme distributie rechthoekig wordt genoemd.,

voor een uniforme verdeling zijn A en b de parameters.

het aantal boeketten dat dagelijks in een bloemenwinkel wordt verkocht, is gelijkmatig verdeeld, met een maximum van 40 en een minimum van 10.

laten we proberen de kans te berekenen dat de dagelijkse verkopen tussen 15 en 30 zullen dalen.

de kans dat de dagelijkse verkoop zal dalen tussen 15 en 30 is (30-15)*(1/(40-10)) = 0.5

evenzo is de kans dat de dagelijkse omzet groter is dan 20 = 0.,667

het gemiddelde en De variantie van X na een uniforme verdeling is:

de Gemiddelde> E(X) = (a+b)/2

Variantie -> V(X) = (b-a)2/12

De standaard uniforme dichtheid met parameters a = 0 en b = 1, dus de PDF voor standaard uniforme dichtheid wordt gegeven door:

Binomiale Verdeling

Laten we terug gaan naar cricket. Stel dat je de toss vandaag hebt gewonnen en dit duidt op een succesvol evenement. Je gooit weer, maar deze keer heb je verloren., Als je vandaag een toss wint, hoeft dit niet dat je morgen de toss wint. Laten we een willekeurige variabele, zeg X, toewijzen aan het aantal keren dat je de toss hebt gewonnen. Wat kan de mogelijke waarde van X zijn? Het kan elk nummer, afhankelijk van het aantal keren dat je gooide een munt.

er zijn slechts twee mogelijke uitkomsten. Kop geeft succes aan en staart geeft mislukking aan. Daarom kan de kans op het krijgen van een head = 0,5 en de kans op mislukking gemakkelijk worden berekend als: q = 1 – p = 0,5.,

een distributie waarbij slechts twee resultaten mogelijk zijn, zoals succes of mislukking, winst of verlies, winst of verlies en waarbij de kans op succes en mislukking voor alle proeven gelijk is, wordt een binomiale Distributie genoemd.

de uitkomsten hoeven niet even waarschijnlijk te zijn. Herinner je je het voorbeeld van een gevecht tussen mij en de begrafenisondernemer? Dus, als de kans op succes in een experiment 0,2 is dan kan de kans op mislukking gemakkelijk worden berekend als q = 1 – 0,2 = 0,8.

elke proef is onafhankelijk omdat de uitkomst van de vorige toss niet bepalend is voor of invloed heeft op de uitkomst van de huidige toss., Een experiment met slechts twee mogelijke uitkomsten herhaald n aantal keren wordt binomiaal genoemd. De parameters van een binomiale verdeling zijn n en p, waarbij n het totale aantal trials is en p de kans op succes in elke trial.

op basis van de bovenstaande uitleg zijn de eigenschappen van een binomiale distributie

1. elk onderzoek is onafhankelijk.
2. Er zijn slechts twee mogelijke uitkomsten in een studie – een succes of een mislukking.
3. Er wordt een totaal aantal n identieke onderzoeken uitgevoerd.
4. de kans op succes en falen is voor alle onderzoeken hetzelfde., (Proeven zijn identiek.,

   

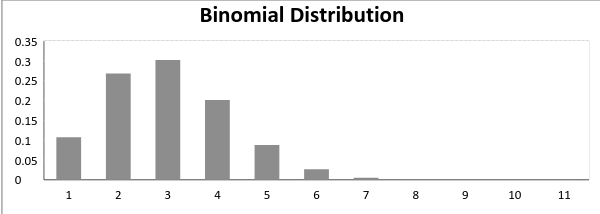
   Nu, wanneer de kans op succes = kans van falen, in een dergelijke situatie is de grafiek van de binomiale verdeling eruit ziet

   

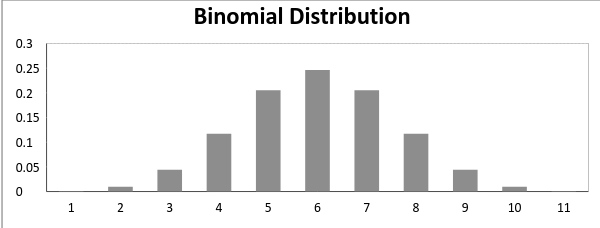
   het gemiddelde en De variantie van de binomiale verdeling wordt gegeven door:

   Bedoel -> µ = n*p

   Variantie -> Var(X) = n*p*q

   Normale Verdeling

   Normale verdeling vertegenwoordigt het gedrag van het merendeel van de situaties in het heelal (Dat is waarom het heet een “normale” verdeling., Ik denk het!). De grote som van (kleine) willekeurige variabelen blijkt vaak normaal verdeeld te zijn, wat bijdraagt aan de wijdverbreide toepassing ervan. Elke verdeling wordt normale verdeling genoemd als deze de volgende kenmerken heeft:

   1. Het gemiddelde, de mediaan en de wijze van verdeling vallen samen.
   2. de curve van de verdeling is klokvormig en symmetrisch over de lijn x=μ.
   3. de totale oppervlakte onder de curve is 1.
   4. precies de helft van de waarden ligt links van het centrum en de andere helft rechts.,

   een normale verdeling verschilt sterk van binomiale verdeling. Echter, als het aantal proeven nadert oneindigheid dan zullen de vormen vrij vergelijkbaar zijn.

   het PDF-bestand van een willekeurige variabele X na een normale verdeling wordt gegeven door:

   

   Het gemiddelde en de variantie van een willekeurige variabele X die normaal zou worden verdeeld, worden gegeven door:

   gemiddelde- > E(X) = µ

   variantie – > var(x) = σ^2

   hier zijn µ (gemiddelde) en σ (standaardafwijking) de parameters.,
   de grafiek van een willekeurige variabele X ~ N (µ, σ) is hieronder weergegeven.

   

   een standaard normale verdeling wordt gedefinieerd als de verdeling met gemiddelde 0 en standaardafwijking 1. Voor een dergelijk geval wordt de PDF:

   

   

   Poisson distributie

   stel dat u in een callcenter werkt, hoeveel gesprekken krijgt u ongeveer per dag? Het kan elk nummer zijn. Nu, het hele aantal gesprekken in een callcenter in een dag wordt gemodelleerd door Poisson distributie., Enkele andere voorbeelden zijn

   1. het aantal noodoproepen dat in een ziekenhuis per dag wordt opgenomen.
   2. het aantal diefstallen dat op een dag in een gebied is gemeld.
   3. het aantal klanten dat binnen een uur bij een salon aankomt.
   4. het aantal zelfmoorden in een bepaalde stad.
   5. het aantal afdrukfouten op elke pagina van het boek.

   U kunt nu vele voorbeelden bedenken die dezelfde cursus volgen., Poisson distributie is van toepassing in situaties waarin gebeurtenissen plaatsvinden op willekeurige punten van tijd en ruimte waarin ons belang ligt alleen in het aantal gebeurtenissen van de gebeurtenis.

   een distributie wordt poissondistributie genoemd wanneer de volgende veronderstellingen geldig zijn:

   1. Een succesvol evenement mag de uitkomst van een ander succesvol evenement niet beïnvloeden.
   2. De kans op succes over een kort interval moet gelijk zijn aan de kans op succes over een langer interval.
   3. De kans op succes in een interval nadert nul als het interval kleiner wordt.,

   als een distributie bovenstaande veronderstellingen valideert, dan is het een Poisson distributie. Sommige notaties die gebruikt worden in de distributie van Poisson zijn:

   • λ is de snelheid waarmee een gebeurtenis optreedt,
   • t is de lengte van een tijdsinterval,
   • en X is het aantal gebeurtenissen in dat tijdsinterval.

   Hier wordt X een Poisson-willekeurige variabele genoemd en de kansverdeling van X wordt Poisson-Distributie genoemd.

   zij µ geeft het gemiddelde aantal gebeurtenissen aan in een interval van lengte t. vervolgens µ = λ * t.,

   de PMF van X na een poissondistributie wordt gegeven door:

   

   De gemiddelde µ is de parameter van deze distributie. µ wordt ook gedefinieerd als λ maal de lengte van dat interval. De grafiek van een Poissondistributie is hieronder weergegeven:

   

   de grafiek hieronder illustreert de verschuiving in de curve als gevolg van de toename van het gemiddelde.

   

   Het is waarneembaar dat naarmate het gemiddelde toeneemt, de curve naar rechts verschuift.,

   Het gemiddelde en de variantie van X na een Poissondistributie:

   gemiddelde -> E(X) = µ
   variantie -> Var(X) = µ

   exponentiële distributie

   call center voorbeeld nog een keer. Hoe zit het met de tijd tussen de gesprekken ? Hier komt de exponentiële distributie ons te hulp. Exponentiële distributie modelleert het tijdsinterval tussen de gesprekken.

   andere voorbeelden zijn:

   1. Lengte van de aankomsttijd van de metro,
   2., Tijdsduur tussen aankomsten bij een benzinestation
   3. De levensduur van een airconditioner

   exponentiële verdeling wordt veel gebruikt voor overlevingsanalyse. Van de verwachte levensduur van een machine tot de verwachte levensduur van een mens, levert exponentiële distributie met succes het resultaat op.

   een willekeurige variabele X zou een exponentiële distributie hebben met PDF:

   f(x) = { λe-λx, x ≥ 0

   en parameter λ>0, wat ook de snelheid wordt genoemd.,

   Voor survival analyse, λ heet de failure rate van een apparaat op elk tijdstip t, gegeven dat het heeft overleefd up-to-t.

   het Gemiddelde en de Variantie van een stochastische variabele X na een exponentiële verdeling:

   Bedoel -> E(X) = 1/λ

   Variantie -> Var(X) = (1/λ)2

   Ook is, hoe groter de snelheid, hoe sneller de curve daalt, en hoe lager het tarief, vlakker de curve. Dit wordt beter uitgelegd met de onderstaande grafiek.,

   

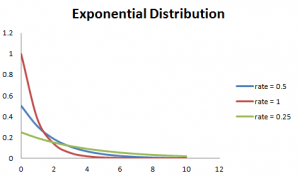
   om de berekening te vergemakkelijken, worden hieronder enkele formules gegeven.
   P{x≤x} = 1 – e-λx, komt overeen met het gebied onder de dichtheidscurve links van x.

   P{X>x} = e-λx, komt overeen met het gebied onder de dichtheidscurve rechts van x.

   P{x1<x≤ x2} = e-λx1 – e-λx2, komt overeen met het gebied onder de dichtheidskromme tussen X1 en X2.

   relaties tussen de distributies

   relatie tussen Bernoulli en binomiale distributie

   1., Bernoulli distributie is een speciaal geval van binomiale distributie met een enkele proef.

   2. Er zijn slechts twee mogelijke uitkomsten van een Bernoulli en binomiale verdeling, namelijk succes en mislukking.

   3. Zowel Bernoulli als binomiale distributies hebben onafhankelijke paden.

   relatie tussen Poisson en binomiale distributie

   Poissondistributie is een limiterend geval van binomiale distributie onder de volgende omstandigheden:

   1. het aantal studies is oneindig groot of n → ∞.,
   2. de kans op succes voor elk onderzoek is hetzelfde en voor onbepaalde tijd klein of p →0.
   3. np = λ, is eindig.

   relatie tussen normale en binomiale distributie& normaal en Poisson distributie:

   normale distributie is een andere beperkende vorm van binomiale distributie onder de volgende omstandigheden:

   1. het aantal studies is oneindig groot, n → ∞.
   2. zowel p als q zijn niet voor onbepaalde tijd klein.

   de normale verdeling is ook een limiterend geval van Poissonverdeling met de parameter λ →∞.,

   relatie tussen exponentiële en Poissondistributie:

   als de tijden tussen willekeurige gebeurtenissen exponentiële distributie volgen met snelheid λ, dan volgt het totale aantal gebeurtenissen in een periode van lengte t de poissondistributie met parameter λt.

   Test uw kennis

   u bent zover gekomen. Nu, bent u in staat om de volgende vragen te beantwoorden? Laat het me weten in de reacties hieronder!

   1. De formule om de standaard normale willekeurige variabele te berekenen is:

   a. (x+µ) / σ
   b. (x-µ) / σ
   c. (x-σ) / µ

   2., In de verdeling van Bernoulli wordt de formule voor de berekening van de standaardafwijking gegeven door:

   a. p (1 – p)
   b. SQRT(p(p – 1))
   c. SQRT(p (1 – p))

   3. Bij een normale verdeling zal een toename van het gemiddelde:

   a. De Kromme naar links verschuiven
   b. De Kromme naar rechts verschuiven
   c.De Kromme plat maken

   4. De levensduur van een batterij wordt exponentieel verdeeld met λ = 0,05 per uur. De kans dat een batterij 10 tot 15 uur meegaat is:

   a. 0. 1341
   b. 0. 1540
   c. 0.,

   End Notes

   kansverdelingen komen voor in vele sectoren, namelijk verzekeringen, natuurkunde, techniek, informatica en zelfs sociale wetenschappen, waar de studenten psychologie en geneeskunde op grote schaal gebruik maken van kansverdelingen. Het heeft een eenvoudige toepassing en wijdverbreid gebruik. Dit artikel belicht zes belangrijke distributies die worden waargenomen in het dagelijks leven en legde de toepassing ervan uit. Nu zul je in staat zijn om deze distributies te identificeren, te relateren en te differentiëren.,

   Als u twijfels hebt en meer artikelen over distributies wilt zien, schrijf dan in de commentaarsectie hieronder. Voor een meer diepgaande schrijf-up van deze distributies, kunt u deze bron raadplegen.