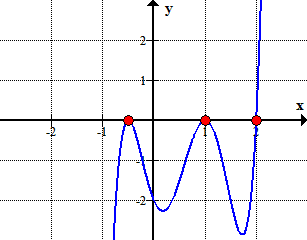
Rational Roots Test(Rational Zeros Theorem 이라고도 함)를 사용하면 다항식의 가능한 모든 rational roots 를 찾을 수 있습니다. A 는 P\left(a\right)=0 을 의미하는 다항식 P\left(x\right)의 루트라고 가정합니다. 즉,a 를 다항식 P\left(x\right)로 대체하고 0,0 을 얻으면 입력 값이 함수의 루트임을 의미합니다.
그러나 우리는 합리적인 뿌리의 가능한 목록을 어떻게 찾습니까? 간단히 말해서 작동하는 방법은 다음과 같습니다!,
키의 아이디어를 합리적 뿌리를 시험
가 있다고 가정하겠습니다 몇 가지 다항 P\left(x\오른쪽)정수 계수와 및 아닌 일정한 기간:
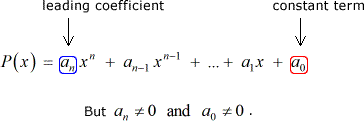
그 모든 합리적인 루트의 P\left(x\오른쪽)의 형태로 되어 있습니다.
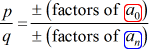
가장 좋은 방법을 배우는 이 방법을 살펴 몇 가지 예!,
Rational Roots Test 를 사용하여 다항식의 Rational Roots 를 찾는 방법의 예
예제 1:Rational Roots Test 를 사용하여 아래의 다항식의 rational roots 를 찾습니다.
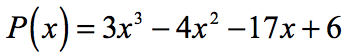
를 찾는 합리적 뿌리(도 알려져 있으로 합리적인 제로)의 다항식과 같은를 찾는 합리적인 x-을 차단.
- 상수 항 a0 및 선행 계수 an 을 식별하여 시작하십시오.,
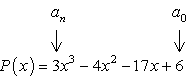
- 결정의 긍정 및 부정적인 요소입니다.
요인의 일정한 기간,{a_0} = 6\,\,:\,\, \이\,\left({1,2,3,6}\right)
요소의 선도기,{a_n} = 3\,\,:\,\, \이\,\left({1,3}\right)
- 목록을 작성의 가능한 합리적 뿌리를 찾아{p\통해 q}단순히 비율의 요소의 지속적인 용어와 선도하는 용어입니다. 가능한 조합을 추적하는지 확인하십시오.,이것이 내가하는 방법입니다. 나는 각 분자를 가져 와서 모든 분모로 나눕니다. 그런 다음 다음 분자로 이동하고 다시 모든 분모로 나눕니다. 나는 모든 분자를 겪을 때까지이 과정을 계속 반복한다. 이것은 우리가 가능한 모든 조합을 다루었 음을 보장합니다.
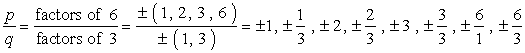
큰 주의:신 후 작성하는 모든 조합,단순화 분수에서의 제거하기 위해 중복.,
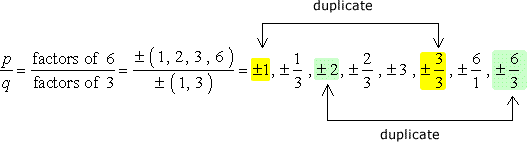
그래서 이들은 이 번호는 중복되지 않는 것으로 확인 가능한 뿌리입니다. 우리는 열두(12)확인 가능한 후보가.
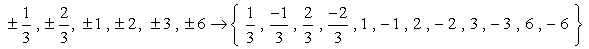
- 기억하는 경우에는 루트의 다항 P\left(x\오른쪽),P\left(\를 오른쪽)=0. 이제 각 번호를 확인합시다.,
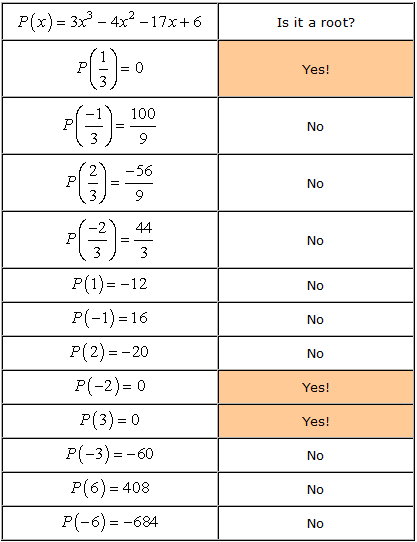
- Therefore, the rational roots of the polynomial
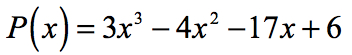
are

Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
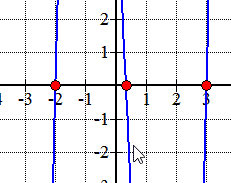
예제 2:을 찾을 합리적의 뿌리가 다항식을 사용하여 아래에 합리적 뿌리 테스트입니다.
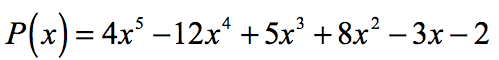
지속적인 용어 a0=-2 및 그것의 가능한 요인은 p=±1,±2. 선행 계수의 경우,우리는=4 를 가지며 그 요인은 q 입니다= ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
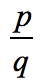
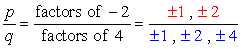
Write down all possible
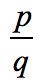
combinations:
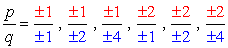
- Simplify each fraction to eliminate duplicates or identical values., 여기에 우리의 새롭고 개선 된 목록이 있습니다!
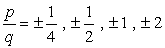
- 때문에 더하거나 빼기 고려하여 각각의 번호,우리는 팔(8)가능자의 뿌리가 이 다항식.
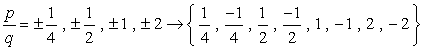
경우 플러그인에서 각각의 가치를 부여 다항 및 면 제한다는 것을 의미하는 번호는 당신이 대체입니다., 종이에 이것을 시도하면이 조건을 만족시키는 세 가지 값만 있다는 것을 확신해야합니다.
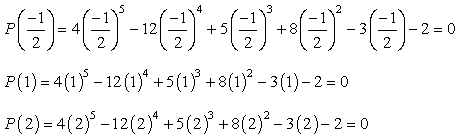
따라서, 합리적의 뿌리가 다항식
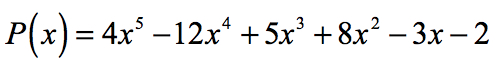
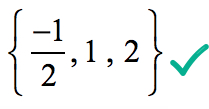
을 그래픽으로 보여줍니다,다항식에 닿거나 십자가 x-axis 에 그 뿌리에 의해 결정된 합리적 뿌리 테스트입니다.,