有理根検定(有理零点定理としても知られている)は、多項式のすべての可能な有理根を見つけることを可能にする。 Aが多項式P\left(x\right)の根であり、p\left(a\right)=0を意味するとします。 言い換えれば、aを多項式P\left(x\right)に代入してゼロ0を得ると、入力値が関数の根であることを意味します。
しかし、合理的な根の可能なリストをどのように見つけるのですか? ここでは、一言で言えばどのように動作するかです!,
有理根検定の重要なアイデア
整数係数と非ゼロ定数項を持つ多項式P\left(x\right)があるとします。
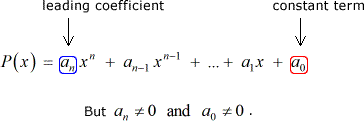
p\left(x\right)のすべての有理根は次の形式になります。
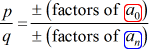
このメソッドを学ぶ最良の方法は、いくつかの例を見てみることです!,
有理根検定を使用して多項式の有理根を見つける方法の例
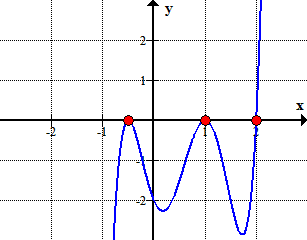
例1:有理根検定を使用して以下の多項式の有理根を見つける。
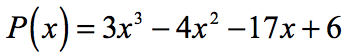
多項式の有理根(有理ゼロとも呼ばれます)を見つけることは、有理x切片を見つけることと同じです。
- 定数項a0と先行係数anを識別することから始めます。,
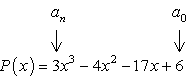
- それぞれの正と負の要因を決定します。
定数項の因子、{a_0} = 6\,\,:\,\, \pm\,\left({1,2,3,6}\right)
主要な用語の要因、{a_n} = 3\,\,:\,\, \pm\,\left({1,3}\right)
- 見つけることによって、可能な有理根のリストを書き留めます{p\over q}これは単に定数項と先行項の因子の比です。 可能な組み合わせを追跡することを確認してください。,
これは私がそれを行う方法です。 私は各分子を取り、それをすべての分母で割ります。 それから私は次の分子に移り、再びすべての分母で割ります。 私はすべての分子を通過するまで、このプロセスを繰り返し続けます。 これは私達がすべての可能な組合せを覆ったことを保障する
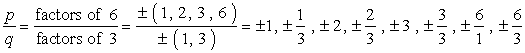
大きな注意:すべての組み合わせを書き留めた後、重複を取り除くために分数を単純化します。,
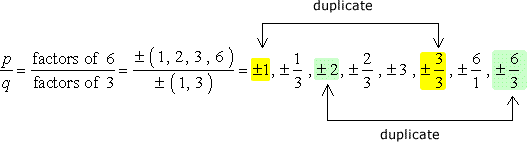
したがって、これらは重複のない数字であり、可能なルーツとしてチェックします。 私たちは、チェックする12の候補を持っています。
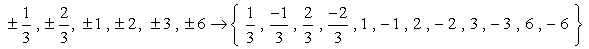
- aが多項式P\left(x\right)の根であれば、P\left(a\right)=0であることを覚えておいてください。 さて、それぞれの番号を確認しましょう。,
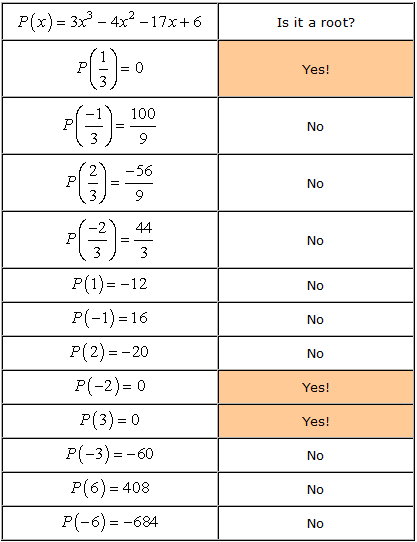
- Therefore, the rational roots of the polynomial
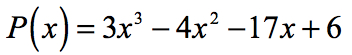
are

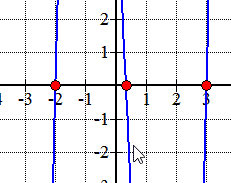
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
例2:有理根検定を使用して、以下の多項式の有理根を求めます。
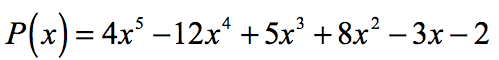
定数項はa0=-2であり、その可能な因子はp=±1、±2である。 先行係数については、an=4であり、その因子はqです= ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
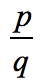
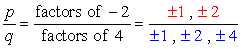
Write down all possible
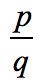
combinations:
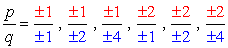
- Simplify each fraction to eliminate duplicates or identical values., こちらは新しいの改善まことにありがとうございます。
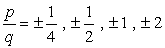
- 各数のプラスまたはマイナスの考慮により、この多項式の根として8つの可能な候補があります。
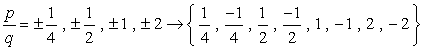
各値を与えられた多項式にプラグインしてゼロになると、置換した数がルートであることを意味します!, 紙の上でこれを試してみて、あなたはこの条件を満たす三つの値しかないと確信する必要があります。
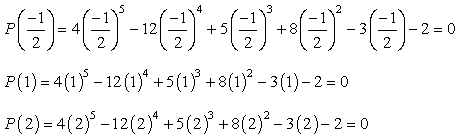
したがって、多項式の有理根
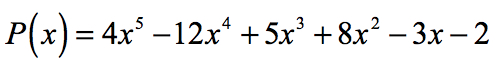
are
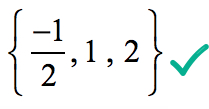
グラフィカルに、多項式が有理根検定によって決定された根でx軸に接するか交差することを示しています。,