Une chose que nous ferons beaucoup avec les algorithmes de cette série est la traversée de graphes. Qu’est-ce que cela signifie exactement?
fondamentalement, L’idée est que nous allons nous déplacer autour du graphe d’un sommet à un autre et découvrir les propriétés de leurs relations interconnectées.
deux des algorithmes les plus couramment utilisés que nous utiliserons beaucoup sont: la recherche en profondeur (DFS) et la recherche en largeur (BFS).,
bien que ces deux algorithmes nous permettent de parcourir des graphes, ils diffèrent de différentes manières. Commençons par DFS.
DFS utilise la philosophie « aller en profondeur, la tête la première” dans sa mise en œuvre. L’idée est qu’à partir d’un sommet initial (ou d’un endroit), nous descendons un chemin jusqu’à la fin et si nous n’atteignons pas notre destination, nous revenons et empruntons un chemin différent.
prenons un exemple., Supposons que nous avons un graphe orienté qui ressemble à ceci:

Maintenant, l’idée est que nous partons au sommet s et on nous demande de trouver le sommet t. À l’aide de DFS, nous allons explorer un chemin, aller tout le chemin à la fin, et si nous ne trouvons pas de t, puis nous descendons par un autre chemin., Voici la procédure à suivre:

Donc, ici, nous descendons le chemin d’accès (p1) de la première voisins vertex et nous voyons que ce n’est pas la fin, car il dispose d’un chemin d’accès vers un autre sommet., Nous avons donc aller dans cette voie:
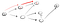
Ce n’est clairement pas le sommet t de sorte que nous devons revenir en arrière, car nous avons atteint une impasse. Puisque le nœud précédent n’a plus de voisins, nous revenons à S., À partir de s, nous allons à sa deuxième voisins d’un nœud:
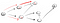
en descendant le chemin d’accès (p2), nous sommes confrontés à trois voisins., Depuis le premier a déjà été visité, nous avons eu à descendre de la seconde:
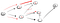
Maintenant, une fois encore, nous avons atteint une impasse qui n’est pas le sommet t de sorte que nous devons revenir en arrière., Puisqu’il y a un autre voisin qui n’a pas été visité, nous descendons voisine chemin et à la fin, nous avons trouvé le sommet t:

C’est comment DFS œuvres. Descendez un chemin et continuez jusqu’à ce que vous ayez atteint la destination ou une impasse. Si c’est la destination, vous avez terminé. Si ce n’est pas le cas, revenez en arrière et continuez sur un chemin différent jusqu’à ce que vous ayez épuisé toutes les options de ce chemin.,
Nous pouvons voir que nous suivons la même procédure à chaque sommet que nous visitons:
Faire un DFS pour chaque voisin du sommet
Depuis, cela implique de faire la même procédure à chaque étape, quelque chose nous dit que nous aurons besoin d’utiliser la récursivité pour mettre en œuvre cet algorithme.
Voici le code en JavaScript:
Remarque: l’algorithme DFS nous permet de déterminer s’il est possible d’aller d’un endroit à l’autre., DFS peut être utilisé de diverses manières et il peut y avoir des changements subtils à l’algorithme ci-dessus. Cependant, le concept général reste le même.
analyse de DFS
analysons maintenant cet algorithme. Puisque nous traversons chaque voisin du nœud et que nous ignorons ceux visités, nous avons un runtime de O(V + E).
Une rapide explication de ce que V+E signifie:
V représente le nombre total de sommets. E représente le nombre total d’arêtes. Chaque sommet a un certain nombre d’arêtes.,
bien qu’il puisse sembler que L’on puisse croire que C’est V•E au lieu de V + E, réfléchissons à ce que V•E signifie exactement.pour que quelque chose soit V•E, cela signifierait que pour chaque sommet, nous devons regarder toutes les arêtes du graphique, que ces arêtes soient ou non connectées à ce sommet spécifique.
alors que, D’autre part, V + E signifie que pour chaque sommet, nous ne regardons que le nombre d’arêtes qui se rapportent à ce sommet. Rappelez-vous du post précédent, que l’espace que nous prenons pour la liste de contiguïté est O(V + E)., Chaque sommet a un certain nombre d’arêtes et dans le pire des cas, si nous devions exécuter DFS sur chaque sommet, nous aurions effectué un travail O(V) en explorant tous les arêtes des sommets, ce qui est O(E). Une fois que nous avons examiné tous les v nombre de Sommets, nous aurions également regardé un total de E arêtes. Par conséquent, c’est V + E.
maintenant, puisque DFS utilise la récursivité sur chaque sommet, cela signifie qu’une pile est utilisée (c’est pourquoi on l’appelle une erreur de débordement de pile chaque fois que vous rencontrez un appel récursif infini). Par conséquent, la complexité de l’espace est O (V).,
voyons maintenant en quoi la recherche en largeur diffère.
recherche de largeur en premier
La recherche de largeur en premier (BFS) suit la philosophie « Go wide, bird’s eye-view”. Ce que cela signifie fondamentalement, c’est qu’au lieu d’aller tout le long d’un chemin jusqu’à la fin, BFS se déplace vers sa destination un voisin à la fois., Regardons ce que cela signifie:

Donc au lieu de simplement aller tout le chemin vers le bas de son premier voisin, BFS allait voir tous les voisins de s en premier et ensuite visiter les voisins les voisins et ainsi de suite jusqu’à ce qu’il atteigne t.,fd17d »> 

See how different DFS and BFS behave?, Alors que j’aime penser que DFS aime aller de front, BFS aime regarder lentement et observer tout une étape à la fois.
maintenant, une question qui nous ressort devrait être: « Comment savons-nous quels voisins visiter en premier des voisins de s? »
Eh bien, nous pourrions utiliser la propriété first-in-first-out (FIFO) d’une file d’attente où nous affichons le premier sommet de la file d’attente, ajoutons ses voisins non visités à la file d’attente, puis poursuivons ce processus jusqu’à ce que la file d’attente soit vide ou que le sommet que nous y ajoutons soit le Sommet,
Maintenant, regardons le code en JavaScript:
l’Analyse de la BFS
Il peut sembler comme BFS est plus lent. Mais si vous regardez attentivement les visualisations DE BFS et DFS, vous constaterez qu’elles ont en fait le même temps d’exécution.
la file d’attente garantit qu’au plus chaque sommet sera traité jusqu’à ce qu’il atteigne la destination. Cela signifie donc qu’au pire des cas, BFS examinera également tous les sommets et toutes les arêtes.,
bien que BFS puisse sembler plus lent, il est en fait jugé plus rapide car si nous devions les implémenter sur des graphiques plus grands, vous constaterez que DFS perd beaucoup de temps à parcourir de longs chemins qui sont finalement faux. En fait, BFS est souvent utilisé dans les algorithmes pour déterminer le chemin le plus court d’un sommet à un autre, mais nous allons les aborder plus tard.
donc, puisque les runtimes sont les mêmes, BFS a un runtime de O(V + E) et en raison de l’utilisation d’une file d’attente qui peut contenir au plus V sommets, il a une complexité d’espace de O(V).,
Analogies à laisser avec
je veux vous laisser avec d’autres façons que j’imagine personnellement comment DFS et BFS fonctionnent dans l’espoir que cela vous aidera à vous souvenir également.
chaque fois que je pense à DFS, j’aime penser à quelque chose qui trouve le bon chemin en se heurtant à beaucoup d’impasses. Habituellement, ce serait comme une souris traversant un labyrinthe pour chercher de la nourriture.,voudrais essayer un chemin, à savoir que le chemin est une impasse, faites-la pivoter vers un autre chemin et répétez ce processus jusqu’à ce qu’il atteigne sa cible:

Et c’est ce que une version simplifiée du processus devrait ressembler à:

Maintenant, pour BFS, J’ai toujours imaginé comme une ondulation.,div>

un peu comme la façon dont BFS commence à la source et des visites de la source voisins de la première et puis s’en va plus vers l’extérieur par la visite de leurs voisins et ainsi de suite:

Résumé
- Depth-First Search (DFS) et la Largeur-Recherche d’Abord (BFS) sont tous deux utilisés pour traverser les graphiques.,
- DFS charge un chemin jusqu’à ce qu’il ait épuisé ce chemin pour trouver sa cible, tandis que BFS se déplace à travers les sommets voisins pour trouver sa cible.
- DFS utilise une pile tandis que BFS utilise une file d’attente.
- DFS et BFS ont un runtime de O(V + E) et une complexité d’espace de O(V).
- Les deux algorithmes ont des philosophies différentes mais partagent la même importance dans la façon dont nous parcourons les graphes.