Distribution des probabilités / types de Distributions

Introduction

Bienvenue dans le monde des probabilités en science des données! Permettez-moi de commencer les choses avec un exemple intuitif.

supposons que vous soyez enseignant dans une université. Après avoir vérifié les devoirs pendant une semaine, vous avez noté tous les étudiants. Vous avez donné ces documents notés à un type de saisie de données à l’université et lui avez dit de créer une feuille de calcul contenant les notes de tous les étudiants., Mais le gars ne stocke que les notes et non les étudiants correspondants.

Il a fait une autre erreur, il a manqué quelques entrées à la hâte et nous n’avons aucune idée des notes manquantes. Trouvons un moyen de résoudre ce problème.

Une façon est que vous visualisez les notes et voir si vous pouvez trouver une tendance dans les données.

Le graphique que vous avez tracé est appelée la fréquence de la distribution des données. Vous voyez qu’il y a une courbe lisse comme structure qui définit nos données, mais remarquez-vous une anomalie?, Nous avons une fréquence anormalement basse à une plage de score particulière. Donc, la meilleure estimation serait d’avoir des valeurs manquantes qui suppriment la dent dans la distribution.

Voici comment vous essayez de résoudre un problème réel en utilisant l’analyse de données. Pour tout Data Scientist, étudiant ou praticien, la distribution est un concept incontournable. Il fournit la base de l’analyse et des statistiques inférentielles.

alors que le concept de probabilité nous donne les calculs mathématiques, les distributions nous aident à visualiser ce qui se passe en dessous.,

dans cet article, j’ai couvert quelques distributions de probabilité importantes qui sont expliquées de manière lucide et complète.

Remarque: Cet article suppose que vous avez une connaissance de base de la probabilité. Sinon, vous pouvez vous référer à ces distributions de probabilité.,

Table des Matières

les principaux Types de Données
Types de Distributions
1. Bernoulli de Distribution
2. une Distribution Uniforme
3. de la Distribution Binomiale
4. Distribution Normale
5. Distribution de Poisson
6. Distribution Exponentielle
les Relations entre les Distributions
Tester vos Connaissances!

types de données courants

avant de passer à l’explication des distributions, voyons quel type de données pouvons-nous rencontrer. Les données peuvent être discrètes ou continues.,

Les données discrètes, comme leur nom l’indique, ne peuvent prendre que des valeurs spécifiées. Par exemple, lorsque vous lancez un dé, les résultats possibles sont 1, 2, 3, 4, 5 ou 6 et non 1,5 ou 2,45.

Les données continues peuvent prendre n’importe quelle valeur dans une plage donnée. La gamme peut être finie ou infinie. Par exemple, le poids ou la taille d’une fille, la longueur de la route. Le poids d’une fille peut être n’importe quelle valeur de 54 kg, ou 54,5 kg, ou 54,5436 kg.

commençons maintenant par les types de distributions.,

types de Distributions

Distribution de Bernoulli

commençons par la distribution la plus simple qui est la Distribution de Bernoulli. C’est en fait plus facile à comprendre qu’il n’y paraît!

vous tous accros au cricket là-bas! Au début d’un match de cricket, comment décidez-vous qui va bat ou balle? Un tirage au sort! Tout dépend si vous gagnez ou perdez le lancer, Non? Disons que si le lancer donne une tête, vous gagnez. Sinon, vous perdez. Il n’y a pas à mi-chemin.

Une distribution de Bernoulli n’a que deux résultats possibles, à savoir 1 (succès) et 0 (échec), et un seul essai., Donc la variable aléatoire X qui a une distribution de Bernoulli peut prendre la valeur 1 avec la probabilité de succès, disons p, et la valeur 0 avec la probabilité de défaillance, dire que le q ou 1-p.

Ici, la survenue d’une tête indique la réussite, et l’apparition d’une queue dénote l’échec.
Probabilité d’obtenir une tête = 0,5 = Probabilité d’obtenir une queue car il n’y a que deux résultats possibles.

la fonction de masse de probabilité est donnée par: px(1-p)1-x où x € (0, 1).,
Il peut également être écrit comme

les probabilités de succès et d’échec ne doivent pas nécessairement être aussi probables, comme le résultat d’un combat entre moi et Undertaker. Il est à peu près certain de gagner. Donc, dans ce cas, la probabilité de mon succès est de 0,15 alors que mon échec est de 0,85

ici, la probabilité de succès(p) n’est pas la même que la probabilité d’échec. Ainsi, le tableau ci-dessous montre la Distribution de Bernoulli de notre combat.

Ici, la probabilité de réussite = 0.15 et de la probabilité de défaillance = 0.85., La valeur attendue est exactement ce que cela semble. Si je te frappe, je peux m’attendre à ce que tu me frappes en arrière. Fondamentalement, la valeur attendue de toute distribution est la moyenne de la distribution., La valeur attendue D’une variable aléatoire X d’une distribution de Bernoulli est trouvée comme suit:

E(X) = 1*p + 0*(1-p) = p

la variance d’une variable aléatoire d’une distribution de bernoulli est:

V(X) = E(X2) – 2 = P – P2 = P(1-p)

il existe de nombreux exemples de distribution de Bernoulli tels que s’il va pleuvoir demain ou non où la pluie dénote le succès et pas de pluie dénote L’échec et gagner (succès) ou perdre (échec) le jeu.

distribution uniforme

lorsque vous lancez un dé équitable, les résultats sont de 1 à 6., Les probabilités d’obtenir ces résultats sont également probables et c’est la base d’une distribution uniforme. Contrairement à la Distribution de Bernoulli, tous les N nombres de résultats possibles d’une distribution uniforme sont également probables.

une variable X est dite uniformément distribuée si la fonction de densité est:

le graphique d’une courbe de distribution uniforme ressemble à

Vous pouvez voir que la forme de la courbe de distribution uniforme est rectangulaire, la raison pour laquelle distribution.,

Pour une Distribution Uniforme, a et b sont les paramètres.

le nombre de bouquets vendus quotidiennement dans un magasin de fleurs est uniformément réparti avec un maximum de 40 et un minimum de 10.

essayons de calculer la probabilité que les ventes quotidiennes tombent entre 15 et 30.

la probabilité que les ventes quotidiennes tombent entre 15 et 30 est (30-15)*(1/(40-10)) = 0.5

de même, la probabilité que les ventes quotidiennes soient supérieures à 20 est = 0.,667

la moyenne et la variance de X suivant une distribution uniforme sont:

Mean -> E(X) = (A+b)/2

Variance -> V(X) = (b-a)2/12

la densité uniforme standard a des Paramètres a = 0 et b = 1, donc le PDF pour la densité uniforme standard est donné par:

distribution binomiale

revenons au cricket. Supposons que vous avez gagné le tirage au sort aujourd’hui et cela indique un événement réussi. Vous lancez à nouveau mais vous avez perdu cette fois., Si vous gagnez un tirage au sort aujourd’hui, cela ne nécessite pas que vous gagnerez le tirage au sort demain. Attribuons une variable aléatoire, disons X, au nombre de fois que vous avez gagné le lancer. Quelle peut être la valeur de X? Il peut s’agir de n’importe quel nombre en fonction du nombre de fois que vous avez lancé une pièce.

Il n’y a que deux résultats possibles. La tête dénotant le succès et la queue dénotant l’échec. Par conséquent, la probabilité d’obtenir une tête = 0,5 et la probabilité d’échec peuvent être facilement calculées comme: q = 1 – p = 0,5.,

une distribution où seulement deux résultats sont possibles, tels que succès ou échec, gain ou perte, victoire ou perte et où la probabilité de succès et d’échec est la même pour tous les essais est appelée Distribution binomiale.

les résultats ne doivent pas nécessairement être aussi probables. Tu te souviens de L’exemple d’une bagarre entre Undertaker et moi? Ainsi, si la probabilité de succès dans une expérience est de 0,2, la probabilité d’échec peut être facilement calculée comme q = 1 – 0,2 = 0,8.

chaque essai est indépendant puisque le résultat du lancer précédent ne détermine ni n’affecte le résultat du lancer actuel., Une expérience avec seulement deux résultats possibles répétés n nombre de fois est appelé binomial. Les paramètres d’une distribution binomiale sont n et p, où n est le nombre total d’essais et p est la probabilité de succès à chaque essai.

Sur la base de l’explication ci-dessus, les propriétés d’une Distribution Binomiale sont

Chaque essai est indépendant.
Il n’y a que deux résultats possibles dans un essai – soit un succès ou un échec.
Un nombre total de n essais identiques sont effectués.
La probabilité de succès et d’échec est de même pour tous les essais., (Essais sont identiques.,

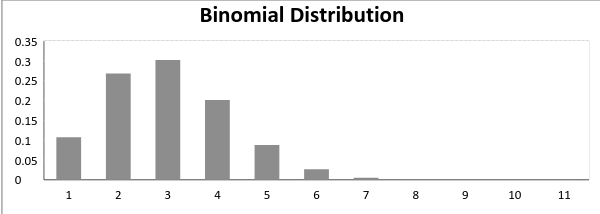
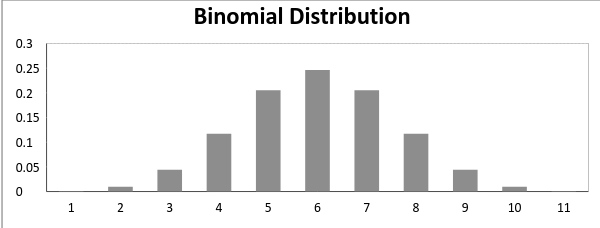
Maintenant, lorsque la probabilité de réussite = probabilité de défaillance, dans une telle situation, le graphique de la distribution binomiale ressemble

la moyenne et La variance d’une distribution binomiale sont donnés par:

Moyenne> µ = n*p

Variance> Var(X) = n*p*q

Distribution Normale

distribution Normale représente le comportement de la plupart des situations dans l’univers (C’est pourquoi on l’appelle un « normal” de la distribution., Je suppose!). La grande somme de (petites) variables aléatoires s’avère souvent normalement distribuée, contribuant à son application généralisée. Toute distribution est appelée distribution normale si elle présente les caractéristiques suivantes:
1. la moyenne, la médiane et le mode de la distribution coïncident.
2. la courbe de la distribution est en forme de cloche et symétrique autour de la droite x=μ.
3. la surface totale sous la courbe est 1.
4. Exactement la moitié des valeurs de la gauche, du centre et l’autre moitié vers la droite.,
Une distribution normale est très différente de la Distribution Binomiale. Cependant, si le nombre d’essais approche l’infini, les formes seront assez similaires.

Le fichier PDF d’une variable aléatoire X suivant une distribution normale est donnée par:

la moyenne et La variance d’une variable aléatoire X qui est dit pour être distribuées normalement est donnée par:

Moyenne> E(X) = µ

la Variance de la> Var(X) = σ^2

Ici, µ (moyenne) et σ (écart-type) sont les paramètres.,
Le graphique d’une variable aléatoire X ~ N (µ, σ) est illustré ci-dessous.

Une distribution normale standard est définie comme la distribution de moyenne 0 et d’écart type 1. Pour de tels cas, le format PDF devient:

Distribution de Poisson

Supposons que vous travaillez dans un centre d’appel, environ combien d’appels obtenez-vous dans une journée? Il peut être n’importe quel nombre. Désormais, le nombre total d’appels dans un centre d’appels par jour est modélisé par la distribution de Poisson., Quelques exemples sont
1. Le nombre d’appels d’urgence à l’hôpital dans un jour.
2. Le nombre de vols déclarés dans une zone sur une journée.
3. Le nombre de clients arrivant dans un salon en une heure.
4. Le nombre de suicides signalés dans une ville donnée.
5. Le nombre d’erreurs d’impression à chaque page du livre.
Vous pouvez maintenant penser à de nombreux exemples suivant le même cours., La Distribution de Poisson est applicable dans les situations où les événements se produisent à des points aléatoires du temps et de l’espace où notre intérêt réside uniquement dans le nombre d’occurrences de l’événement.

Une distribution est appelée distribution de Poisson lorsque les hypothèses suivantes sont valides:

1. Tout événement réussi ne devrait pas influencer le résultat d’un autre événement réussi.
2. La probabilité de succès sur un court intervalle doit être égale à la probabilité de succès sur un intervalle plus long.
3. La probabilité de succès dans un intervalle approche de zéro à mesure que l’intervalle devient plus petit.,

maintenant, si une distribution valide les hypothèses ci-dessus, alors c’est une distribution de Poisson. Quelques notations utilisées dans la distribution de Poisson sont:
- λ est la vitesse à laquelle un événement se produit,
- t est la longueur de l’intervalle de temps
- Et X est le nombre d’événements dans cet intervalle de temps.
ici, X est appelée une Variable aléatoire de Poisson et la distribution de probabilité de X est appelée distribution de Poisson.

soit µ le nombre moyen d’événements dans un intervalle de longueur T. ensuite, µ = λ*T.,

Le CMR de X suivant une distribution de Poisson est donnée par:

La moyenne µ est le paramètre de cette distribution. µ est également défini comme la longueur λ fois de cet intervalle. Le graphique d’une distribution de Poisson est indiqué ci-dessous:

Le graphique ci-dessous illustre le décalage de la courbe due à l’augmentation de la moyenne.

Il est perceptible que la moyenne augmente, la courbe se déplace vers la droite.,

la moyenne et La variance de X suivant une distribution de Poisson:

Moyenne> E(X) = µ
la Variance de la> Var(X) = µ

Distribution Exponentielle

prenons le centre d’appel exemple une fois de plus. Ce sujet de l’intervalle de temps entre les appels ? Ici, la distribution exponentielle vient à notre secours. La distribution exponentielle modélise l’intervalle de temps entre les appels.

d’Autres exemples sont:

1. Durée des arrivées en métro,
2., Durée entre les arrivées à une station-service
3. La durée de vie d’un climatiseur

la distribution exponentielle est largement utilisée pour l’analyse de la survie. De la durée de vie attendue d’une machine à la durée de vie attendue d’un humain, la distribution exponentielle fournit avec succès le résultat.

Une variable aléatoire X a une distribution exponentielle avec PDF:

f(x) = { λe-λx, x ≥ 0

et le paramètre λ>0 qui est aussi appelé le taux d’.,

pour l’analyse de survie, λ est appelé taux de défaillance d’un dispositif à tout moment t, étant donné qu’il a survécu jusqu’à T.

Moyenne et Variance D’une variable aléatoire X suivant une distribution exponentielle:

moyenne -> E(x) = 1/λ

variance -> var(x) = (1/λ)2

de plus, plus le taux est élevé, plus la courbe baisse rapidement et plus le taux est bas, flatte la courbe. Ceci est mieux expliqué avec le graphique ci-dessous.,

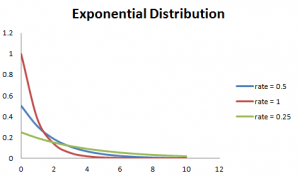
Pour faciliter le calcul, il y a quelques formules données ci-dessous.
P{X≤x} = 1 – e-λx, correspond à l’aire sous la densité de la courbe vers la gauche de x.

P{X>x} = e-λx, correspond à l’aire sous la densité de la courbe à droite de x.

P{x1<X≤ x2} = e-λx1 – e-λx2, correspond à l’aire sous la densité de la courbe entre x1 et x2.

Relations entre les Distributions

Relation entre Bernoulli et Distribution binomiale

1., La Distribution de Bernoulli est un cas particulier de Distribution binomiale avec un seul essai.

2. Il n’y a que deux résultats possibles d’une distribution de Bernoulli et binomiale, à savoir le succès et l’échec.

3. Les Distributions Bernoulli et binomiales ont toutes deux des traînées indépendantes.

Relation entre Poisson et Distribution binomiale

la Distribution de Poisson est un cas limite de distribution binomiale dans les conditions suivantes:
1. Le nombre d’essais est indéfiniment grand ou n → ∞.,
2. la probabilité de succès pour chaque essai est la même et indéfiniment petite ou p →0.
3. np = λ, est finie.
Relation entre la Distribution normale et la distribution binomiale& Distribution normale et de Poisson:

la distribution normale est une autre forme limitative de la distribution binomiale dans les conditions suivantes:
1. Le nombre d’essais est indéfiniment grand, n → ∞.
2. p et q ne sont pas indéfiniment petit.
la distribution normale est aussi un cas limite de la distribution de Poisson avec le paramètre λ →∞.,

Relation entre la distribution exponentielle et la Distribution de Poisson:

Si les temps entre les événements aléatoires suivent la distribution exponentielle avec le taux λ, alors le nombre total d’événements dans une période de temps de longueur t suit la distribution de Poisson avec le paramètre λt.

Testez vos connaissances

Vous êtes arrivé à ce stade. Maintenant, êtes-vous en mesure de répondre aux questions suivantes? Laissez-moi savoir dans les commentaires ci-dessous!

1. La formule pour calculer la variable aléatoire normale standard est:

un. (x+µ) / σ
b. (x-µ) / σ
c. (x-σ) / µ

2., Dans la Distribution de Bernoulli, la formule de calcul de l’écart type est donnée par:

A. p (1 – p)
B. SQRT(p(p – 1))
C. SQRT(p(1 – p))

3. Pour une distribution normale, une augmentation de la moyenne sera:

un. décalage de la courbe vers la gauche
b. décalage de la courbe vers la droite
c. aplatir la courbe

4. La durée de vie d’une batterie est répartie de manière exponentielle avec λ = 0,05 par heure. La probabilité qu’une batterie dure entre 10 et 15 heures est:

A. 0.1341
B. 0.1540
C. 0.,0079

notes de fin

Les Distributions de probabilité sont répandues dans de nombreux secteurs, à savoir l’assurance, la physique, l’ingénierie, l’informatique et même les sciences sociales où les étudiants en psychologie et en médecine utilisent largement les distributions de probabilité. Il a une application facile et une utilisation généralisée. Cet article a mis en évidence six distributions importantes qui sont observées dans la vie quotidienne et expliqué leur application. Maintenant, vous serez en mesure d’identifier, de relier et de différencier entre ces distributions.,

Si vous avez des doutes et que vous voulez voir plus d’articles sur les distributions, veuillez écrire dans la section commentaire ci-dessous. Pour une rédaction plus approfondie de ces distributions, vous pouvez vous référer à cette ressource.