Järkevä Juuret Testi (tunnetaan myös nimellä Järkevä Nollia Lause) avulla voimme löytää kaikki mahdolliset rationaaliset juuret polynomin. Oletetaan, että A on polynomin P\left( x \right) juuri, joka tarkoittaa P\left( a \right) = 0. Toisin sanoen, jos me korvata osaksi polynomi P\left( x \right) ja saada nolla, 0, se tarkoittaa, että tulon arvo on root toiminto.
mutta miten löydämme mahdollisen listan rationaalisista juurista? Näin se toimii pähkinänkuoressa!,
– Näppäintä Järkevään Juuret Testi
Oletetaan, että meillä on jokin polynomi P\left( x \right) kanssa integer kertoimia ja nollasta poikkeava vakio aikavälillä:
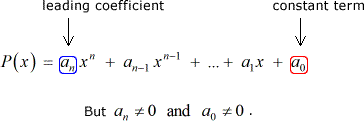
Sitten jokainen järkevä root P\left( x \right) on muotoa:
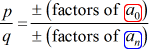
paras tapa oppia tämä tapa on katsomaan joitakin esimerkkejä!,
Esimerkkejä siitä, Miten Löytää Järkevä Juuret Polynomi käyttämällä Järkevä Juuret Testi
Esimerkki 1: Etsi järkevä juuret polynomin alla käyttämällä Järkevä Juuret Testi.
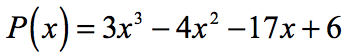
Löytää järkevä juuret (tunnetaan myös nimellä järkevä nollia) on polynomi on sama kuin löytää järkevä x-kuuntelevansa.
- Aloita tunnistamalla vakiotermi a0 ja johtava kerroin an.,
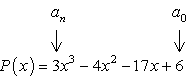
- Määrittää positiiviset ja negatiiviset tekijät kunkin.
Tekijät vakiotermi, {a_0} = 6\,\,:\,\, \pm \,\left( {1,2,3,6} \right)
Tekijät johtavat aikavälillä, {a_n} = 3\,\,:\,\, \pm \,\left( {1,3} \right)
- Kirjoita luettelo mahdollisista järkevä juuret etsimällä {p \over q}, joka on yksinkertaisesti liian tekijöitä vakiotermi ja johtava termi. Varmista, että pidät kirjaa mahdollisista yhdistelmistä.,
This is how I do it. Otan jokaisen osoittajan ja jaan sen kaikkien nimittäjien kesken. Sitten siirryn seuraavaan osoittajaan ja jaan jälleen kaikki nimittäjät. Toistan tätä prosessia, kunnes olen käynyt läpi kaikki osoittajat. Näin varmistetaan, että olemme kattaneet kaikki mahdolliset yhdistelmät.
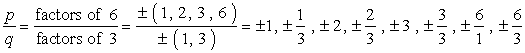
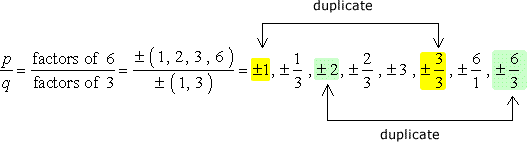
ISO Huomio: Kun olet kirjoittanut alas kaikki yhdistelmät, yksinkertaistaa jakeet, jotta päästä eroon kaksoiskappaleet.,
Niin, nämä numerot ilman kaksoiskappaleita, että me tarkistaa kuin mahdollista juuret. Meillä on kaksitoista (12) mahdollista ehdokasta tarkistettavana.
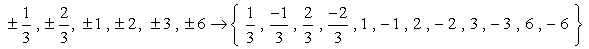
- Muista, että jos a on juuri polynomin P\left( x \right), niin P\left( a \right) = 0. Tarkistetaan jokainen numero.,
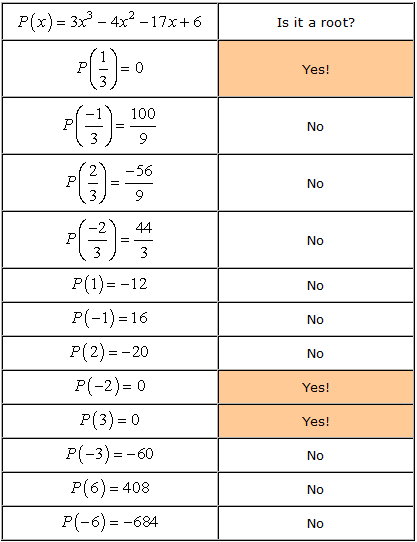
- Therefore, the rational roots of the polynomial
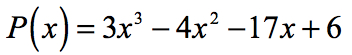
are

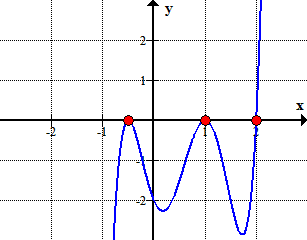
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
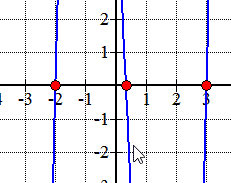
Esimerkki 2: Etsi järkevä juuret polynomin alla käyttäen Järkevä Juuret Testi.
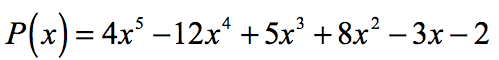
vakiotermi on a0 = -2 ja sen mahdollisia tekijöitä ovat p = ± 1, ± 2. Johtavalle kertoimelle meillä on = 4 ja sen tekijät ovat q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
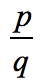
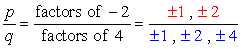
Write down all possible
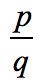
combinations:
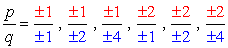
- Simplify each fraction to eliminate duplicates or identical values., Tässä on uusi ja parannettu lista!
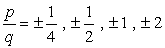
- Koska plus tai miinus huomioon kunkin numeron, meillä on kahdeksan (8) mahdollisia ehdokkaita, koska juuret tämän polynomi.
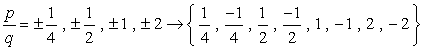
Jos liität kunkin arvo on annettu polynomi ja saa nolla, se tarkoittaa, että määrä teidän substituoitu on root!, Kokeile tätä paperilla, ja sinun pitäisi olla vakuuttunut siitä, että on vain kolme arvoa, jotka täyttävät tämän ehdon.
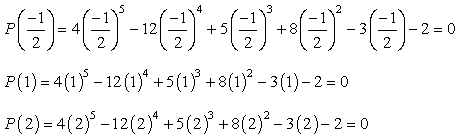
näin Ollen, järkevä juuret polynomin
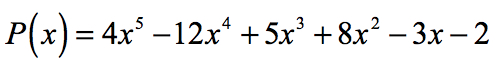
ovat
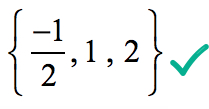
Graafisesti, se osoittaa, että polynomi koskettaa tai läpäisee x-akselin ne juuret määräytyy järkevä juuret testi.,