la prueba de raíces racionales (también conocida como Teorema de ceros racionales) nos permite encontrar todas las raíces racionales posibles de un polinomio. Supongamos que a es la raíz del polinomio P \ left( x \right) que significa P\left (a \right) = 0. En otras palabras, si sustituimos a en el polinomio P \ left(x \ right) y obtenemos cero, 0, significa que el valor de entrada es una raíz de la función.
Pero ¿cómo encontramos la posible Lista de raíces racionales? Así es como funciona en pocas palabras!,
las Ideas principales de Raíces Racionales de Prueba
Supongamos que tenemos algunos polinomio P\left( x \right) con coeficientes enteros y un término constante diferente de cero:
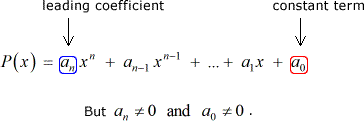
a Continuación, cada racional raíz de P\left( x \right) es de la forma:
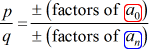
La mejor manera de aprender este método es tomar un vistazo a algunos ejemplos!,
ejemplos de cómo encontrar las raíces racionales de un polinomio utilizando la prueba de raíces racionales
Ejemplo 1: Encuentre las raíces racionales del polinomio a continuación utilizando la prueba de raíces racionales.
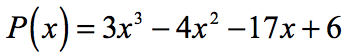
Encontrar las raíces racionales (también conocido como ceros racionales de un polinomio es el mismo que encontrar el racional interceptos en x.
- comience identificando el término constante A0 y el coeficiente principal an.,
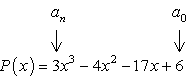
- Determinar los factores positivos y negativos de cada uno.
factores de término constante, {a_0} = 6\,\,:\,\, \pm \, \left( {1,2,3,6} \ right)
factores del término principal, {a_n} = 3\,\,:\,\, \pm \, \ left ({1,3} \right)
- escriba la lista de las posibles raíces racionales encontrando {p \sobre q} que es simplemente la relación de los factores del término constante y el término principal. Asegúrese de llevar un registro de las posibles combinaciones.,
así es como lo hago. Tomo cada numerador y lo divido por todos los denominadores. Luego paso al siguiente numerador y nuevamente divido por todos los denominadores. Sigo repitiendo este proceso hasta que he pasado por todos los numeradores. Esto asegura que hemos cubierto todas las combinaciones posibles.
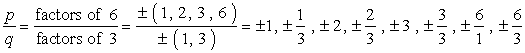
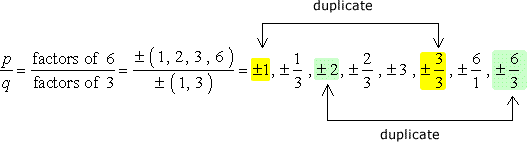
BIG Precaución: Después de escribir todas las combinaciones, simplificar las fracciones con el fin de deshacerse de los duplicados.,
Así que estos son los números sin duplicados que vamos a comprobar como sea posible de las raíces. Tenemos doce (12) posibles candidatos para verificar.
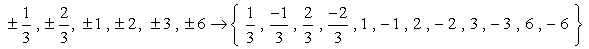
- Recuerde que si a es una raíz del polinomio P\left( x \right), entonces P\left( a \derecho) = 0. Ahora, comprobemos cada número.,
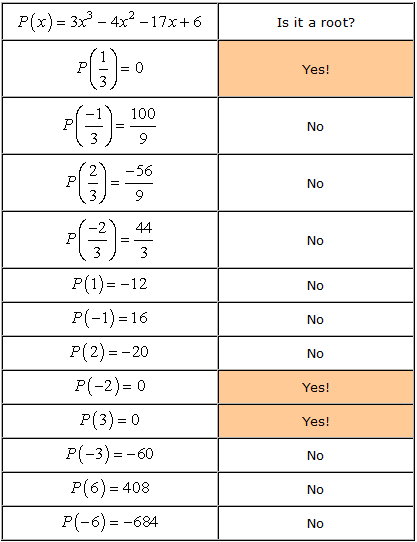
- Therefore, the rational roots of the polynomial
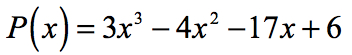
are

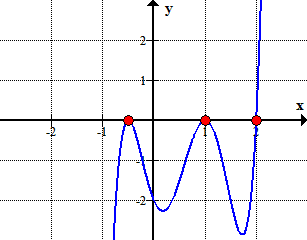
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
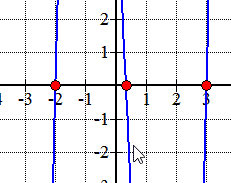
Ejemplo 2: Encuentre las raíces racionales del polinomio a continuación utilizando la prueba de raíces racionales.
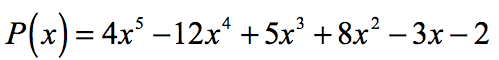
El término constante a0 = -2 y sus posibles factores son p = ± 1, ± 2. Para el coeficiente principal, tenemos an = 4 y sus factores son q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
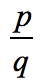
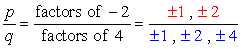
Write down all possible
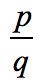
combinations:
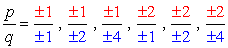
- Simplify each fraction to eliminate duplicates or identical values., Aquí está nuestra lista nueva y mejorada!
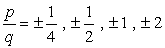
- Debido a la más o menos la consideración de cada número, vamos a tener ocho (8) posibles candidatos como las raíces de este polinomio.
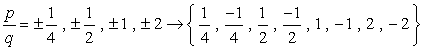
Si usted conecta en cada valor del polinomio y se pone a cero, significa que el número que usted sustituido es una raíz!, Pruebe esto en papel, y debe estar convencido de que solo hay tres valores que satisfacen esta condición.
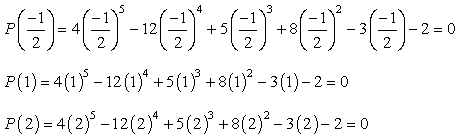
por lo Tanto, las raíces racionales del polinomio
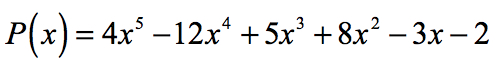
son
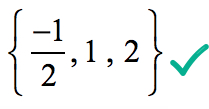
de forma Gráfica, muestra que el polinomio toca o cruza el eje de x en esas raíces determinado por racionales de las raíces de la prueba.,