Rational Roots Test (også kendt som Rational Zeros Theorem) giver os mulighed for at finde alle mulige rationelle rødder i et polynomium. Antag, at a er roden til polynomet p \ venstre (\\højre), der betyder P \venstre (a \ højre) = 0. Med andre ord, hvis vi erstatter a i polynomet p\left (\\right) og får nul, 0, betyder det, at inputværdien er en rod af funktionen.
men hvordan finder vi den mulige liste over rationelle rødder? Sådan fungerer det i et nøddeskal!,
– Tasten Ideer af Rationelle Rødder Test
Antag at vi har nogle polynomium P\left( x \right) med heltal koefficienter og en konstant forskellig fra nul sigt:
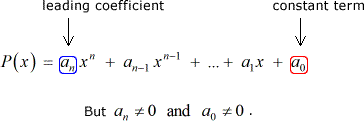
Så hver rational rod i P\left( x \right) er af formen:
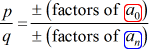
Den bedste måde at lære denne metode er at tage et kig på nogle eksempler!,
eksempler på, hvordan man finder de rationelle rødder i et polynom ved hjælp af Rational Roots Test
eksempel 1: Find de rationelle rødder i polynomet nedenfor ved hjælp af Rational Roots Test.
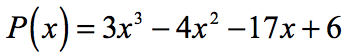
Finde den rationelle rødder (også kendt som en rationel nuller) af et polynomium er det samme som at finde en rationel x-aflytninger.
- Start med at identificere det konstante udtryk a0 og den førende koefficient an.,
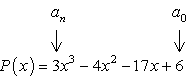
- Bestemme den positive og negative faktorer for hver.
Faktorer konstant sigt, {a_0} = 6\,\,:\,\, \pm \,\left( {1,2,3,6} \right)
Faktorer, der fører sigt, {a_n} = 3\,\,:\,\, \pm \,\left( {1,3} \right)
- Skriv en liste over de mulige rationelle rødder ved at finde {p \over q} der er simpelthen forholdet mellem de faktorer, der er af den konstante sigt og fører sigt. Sørg for at holde styr på de mulige kombinationer.,
Sådan gør jeg det. Jeg tager hver tæller og deler den med alle nævnere. Så går jeg videre til den næste tæller og deler igen med alle nævnere. Jeg fortsætter med at gentage denne proces, indtil jeg har gennemgået alle tællerne. Dette sikrer, at vi har dækket alle mulige kombinationer.
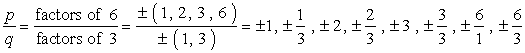
STOR Forsigtighed: Når du skrive ned alle kombinationer, forenkle de fraktioner, for at slippe af dubletter.,
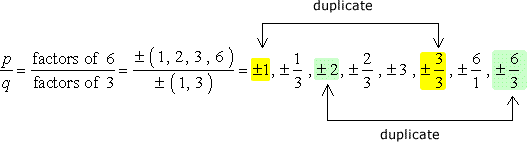
Så det er disse numre, uden dubletter, som vi vil ind som muligt rødder. Vi har tolv (12) mulige kandidater til at kontrollere.
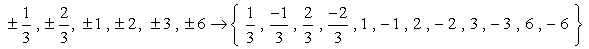
- Husk, at hvis a er en rod i polynomiet P\left( x \right), så er P\left( a \right) = 0. Lad os nu tjekke hvert nummer.,
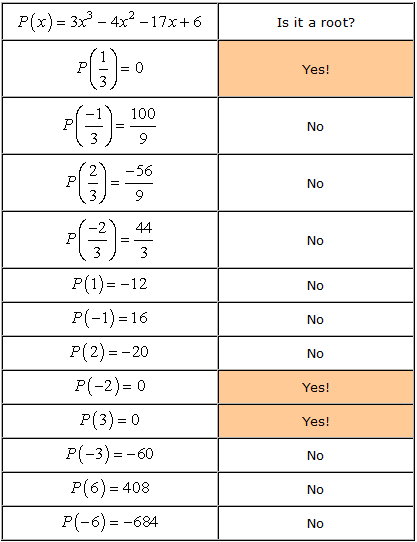
- Therefore, the rational roots of the polynomial
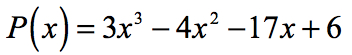
are

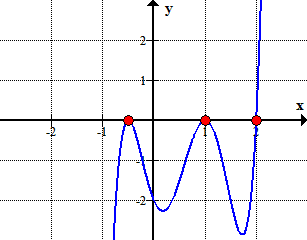
Here is the graph of the polynomial showing where it crosses or touches the x-axis. These are in fact the x-intercepts of the polynomial.,
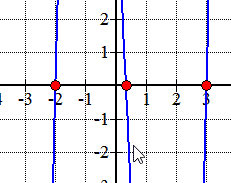
Eksempel 2: Find den rationelle rødder i polynomiet nedenfor ved hjælp af Rationelle Rødder Test.
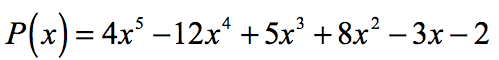
Den konstante udtryk er a0 = -2 og dens mulige faktorer er p = ± 1, ± 2. For den førende koefficient har vi en = 4, og dens faktorer er q = ± 1, ± 2, ± 4.,
- To find the possible roots of the polynomial, write in the form
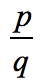
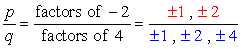
Write down all possible
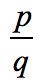
combinations:
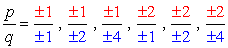
- Simplify each fraction to eliminate duplicates or identical values., Her er vores nye og forbedrede liste!
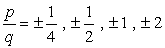
- på Grund af plus-eller minus overvejelse af hvert nummer, vi vil have otte (8) mulige kandidater, som rødderne i dette polynomium.
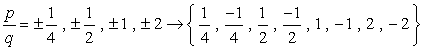
Hvis du sætter et stik i hver værdi, at det givne polynomium og bliver nul, betyder det nummer, du substitueret er en rod!, Prøv dette på papir, og du bør være overbevist om, at der kun er tre værdier, der opfylder denne betingelse.
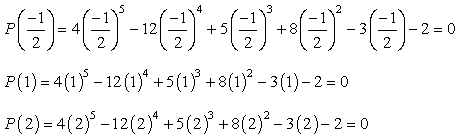
Derfor, den rationelle rødder i polynomiet
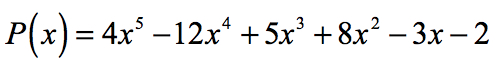
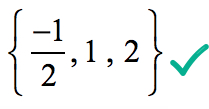
i Grafisk, for det viser, at polynomiet rører eller krydser x-aksen på disse rødder bestemmes af rationelle rødder test.,