på denna sida beskriver vi de tre principer du bör förstå när det gäller seriekretsar:
- ström: mängden ström är densamma genom någon komponent i en seriekrets.
- motstånd: det totala motståndet hos någon seriekrets är lika med summan av de enskilda resistanserna.
- spänning: matningsspänningen i en seriekrets är lika med summan av de enskilda spänningsfallen.,
Låt oss ta en titt på några exempel på seriekretsar som visar dessa principer.
vi börjar med en seriekrets bestående av tre motstånd och ett enda batteri:

den första principen att förstå om seriekretsar är följande:
mängden ström i en seriekrets är densamma genom någon komponent i kretsen.
detta beror på att det bara finns en väg för strömflöde i en seriekrets., Eftersom elektrisk laddning strömmar genom ledare som kulor i ett rör, måste flödeshastigheten (marmorhastighet) vid vilken punkt som helst i kretsen (röret) vid vilken specifik tidpunkt som helst vara lika.
med hjälp av Ohms lag i seriekretsar
från det sätt som 9-voltsbatteriet är ordnat kan vi säga att strömmen i denna krets kommer att flöda medurs, från punkt 1 till 2 till 3 till 4 och tillbaka till 1. Vi har dock en spänningskälla och tre motstånd. Hur använder vi Ohms lag här?,
en viktig varning till Ohms lag är att alla kvantiteter (spänning, ström, motstånd och kraft) måste relatera till varandra när det gäller samma två punkter i en krets. Vi kan se detta koncept i aktion i exemplet med single resistor circuit nedan.,
med hjälp av Ohms lag i en enkel, enda Resistorkrets
med ett enda batteri, enmotståndskrets, kunde vi enkelt beräkna vilken mängd som helst eftersom de alla applicerades på samma två punkter i kretsen:


eftersom punkterna 1 och 2 är anslutna tillsammans med en enda Resistorkrets
råden av försumbar motstånd, liksom punkterna 3 och 4, kan vi säga att punkt 1 är elektriskt vanligt att punkt 2, och att punkt 3 är elektriskt vanligt att punkt 4., Eftersom vi vet att vi har 9 Volt elektromotorisk kraft mellan punkterna 1 och 4 (direkt över batteriet), och eftersom punkt 2 är gemensam för punkt 1 och punkt 3 gemensam för punkt 4, måste vi också ha 9 volt mellan punkterna 2 och 3 (direkt över motståndet).
därför kan vi tillämpa Ohms lag (I = E/R) på strömmen genom motståndet, eftersom vi känner till spänningen (E) över motståndet och motståndet (R) hos det motståndet. Alla termer (E, I, R) gäller för samma två punkter i kretsen, till samma motstånd, så vi kan använda Ohms lagformel utan reservation.,
med hjälp av Ohms lag i kretsar med flera motstånd
i kretsar som innehåller mer än ett motstånd måste vi vara försiktiga med hur vi tillämpar Ohms lag. I tremotståndsexempelkretsen nedan vet vi att vi har 9 volt mellan punkterna 1 och 4, vilket är mängden elektromotorisk kraft som driver strömmen genom seriekombinationen R1, R2 och R3. Vi kan dock inte ta värdet på 9 volt och dela det med 3k, 10k eller 5k Ω för att försöka hitta ett strömvärde, eftersom vi inte vet hur mycket spänning som finns över någon av dessa motstånd, individuellt.,

siffran 9 Volt är en total mängd för hela kretsen, medan siffrorna 3k, 10k och 5k Ω är individuella kvantiteter för enskilda motstånd. Om vi skulle ansluta en siffra för total spänning till en Ohms lag ekvation med en siffra för individuellt motstånd, skulle resultatet inte relatera exakt till någon kvantitet i den verkliga kretsen.,
för R1 kommer Ohms lag att relatera mängden spänning över R1 med strömmen genom R1, med tanke på R1: S motstånd, 3kω:

men eftersom vi inte känner till spänningen över R1 (endast den totala spänningen som levereras av batteriet över kombinationen av tremotstånd) och vi vet inte strömmen genom R1, kan vi inte göra några beräkningar med någon formel. Detsamma gäller för R2 och R3: vi kan tillämpa Ohms lag ekvationer om och endast om alla villkor är representativa för sina respektive kvantiteter mellan samma två punkter i kretsen.,
Så vad kan vi göra? Vi vet spänningen hos källan (9 Volt) applicerad över seriens kombination av R1, R2 och R3, och vi vet motståndet hos varje motstånd, men eftersom dessa kvantiteter inte är i samma sammanhang kan vi inte använda Ohms lag för att bestämma kretsströmmen. Om vi bara visste vad det totala motståndet var för kretsen: då kunde vi beräkna den totala strömmen med vår figur för total spänning (I=E/R).,
kombinera flera motstånd till ett ekvivalent totalt motstånd
detta leder oss till den andra principen för seriekretsar:
den totala resistansen hos någon seriekrets är lika med summan av de enskilda resistanserna.
detta bör göra intuitiv mening: ju fler motstånd i serie som strömmen måste strömma igenom, desto svårare blir det för strömmen att flöda.,
i exempelproblemet hade vi ett 3 kΩ, 10 kΩ och 5 kω-motstånd i serie, vilket ger oss ett totalt motstånd på 18 kΩ:

i huvudsak har vi beräknat motsvarande motstånd för R1, R2 och R3 kombinerat.,oltages med Hjälp av Ohms Lag
att Veta att strömmen är lika genom alla delar av en serie krets (och vi har precis bestämt ström genom batteriet), kan vi gå tillbaka till vår ursprungliga krets schema och observera aktuell genom varje komponent:
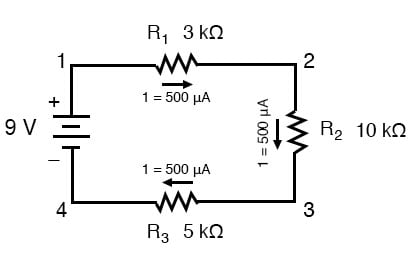
Nu att vi vet hur mycket ström genom varje motstånd, kan vi använda Ohms Lag för att bestämma spänningsfallet över var och en (genom att tillämpa Ohms Lag i dess rätta sammanhang):

observera att spänningen sjunker över varje motstånd, och hur summan av spänningen sjunker (1.,5 + 5 + 2.5) är lika med batteriet (matningsspänning) spänning: 9 Volt.
detta är den tredje principen för seriekretsar:
matningsspänningen i en seriekrets är lika med summan av de enskilda spänningsfallen.
analysera enkla seriekretsar med ”Tabellmetoden” och Ohms lag
den metod vi just använde för att analysera denna enkla seriekrets kan dock strömlinjeformas för bättre förståelse., Genom att använda en tabell för att lista alla spänningar, strömmar och motstånd i kretsen blir det väldigt lätt att se vilka av dessa kvantiteter som kan vara korrekt relaterade i någon Ohms Lagekvation:

regeln med en sådan tabell är att endast tillämpa Ohms lag på värdena inom varje vertikal kolumn. Till exempel, ER1 bara med IR1 och R1, ER2 bara med IR2 och R2, etc., Du börjar din analys genom att fylla i de delar av tabellen som ges till dig från början:

som du kan se från arrangemanget av data kan vi inte tillämpa 9 Volt ET (total spänning) på någon av resistanserna (R1, R2 eller R3) i någon Ohms Lagformel eftersom de är i olika kolumner. Batterispänningens 9 Volt appliceras inte direkt över R1, R2 eller R3. Vi kan dock använda våra” regler ” av seriekretsar för att fylla i tomma fläckar på en horisontell rad.,

då, med vetskap om att strömmen delas lika av alla komponenter i en seriekrets (en annan ”regel” av seriekretsar), kan vi fylla i strömmarna för varje motstånd från den aktuella siffran som just beräknats:

slutligen kan vi använda Ohms lag för att bestämma spänningsfallet över hela världen.varje motstånd, en kolumn i taget:

verifiera beräkningar med computer analysis (Spice)
bara för skojs skull kan vi använda en dator för att analysera samma krets automatiskt., Det kommer att vara ett bra sätt att verifiera våra beräkningar och också bli mer bekant med datoranalys. Först måste vi beskriva kretsen till datorn i ett format som känns igen av programvaran.
SPICE-programmet vi kommer att använda kräver att alla elektriskt unika punkter i en krets numreras, och komponentplacering förstås av vilka av de numrerade punkterna eller” noder ” som de delar. För tydlighetens skull numrerade jag de fyra hörnen av vårt exempel krets 1 till 4., SPICE kräver dock att det finns en nod noll någonstans i kretsen, så jag ska rita om kretsen, ändra numreringsschemat något:

allt jag har gjort här är omnumrerat det nedre vänstra hörnet av kretsen 0 istället för 4. Nu kan jag skriva in flera rader text i en datorfil som beskriver kretsen i termer SPICE kommer att förstå, komplett med ett par extra rader kod styra programmet för att visa spänning och aktuella data för vår visning nöje., Den här datorfilen är känd som netlist i SPICE terminologi:
series circuit v1 1 0 r1 1 2 3k r2 2 3 10k r3 3 0 5k .dc v1 9 9 1 .print dc v(1,2) v(2,3) v(3,0) .end
nu behöver jag bara köra SPICE-programmet för att bearbeta netlist och mata ut resultaten:
| v1 | v(1,2) | v(1,2) | v(3) | i(v1) |
|---|---|---|---|---|
| 9.000 E+00 | 1.500 E+00 | 5.000 e+00 | 2.500 e+00 | -5.,000E-04 |
den här utskriften berättar att batterispänningen är 9 volt och spänningen sjunker över R1, R2 och R3 är 1,5 volt, 5 volt respektive 2,5 volt. Spänningsfall över någon komponent i SPICE refereras av nodnummer komponenten ligger mellan, så v (1,2) refererar spänningen mellan noderna 1 och 2 i kretsen, vilka är de punkter mellan vilka R1 är belägen.,
ordningen på nodnummer är viktig: när SPICE matar ut en siffra för v (1,2), betraktar den polariteten på samma sätt som om vi höll en voltmeter med den röda testledningen på nod 1 och den svarta testledningen på nod 2. Vi har också en display som visar ström (om än med ett negativt värde) vid 0,5 milliamps eller 500 mikroamps. Så vår matematiska analys har bekräftats av datorn. Denna siffra visas som ett negativt tal i KRYDDANALYSEN, på grund av en quirk i hur SPICE hanterar aktuella beräkningar.,
Sammanfattningsvis definieras en seriekrets som endast har en väg genom vilken strömmen kan flöda. Från denna definition följer tre regler för seriekretsar: alla komponenter delar samma ström; resistanser lägger till lika stort, totalt motstånd; och spänningsfall lägger till lika stor, total spänning. Alla dessa regler hittar rot i definitionen av en seriekrets. Om du förstår den definitionen helt, är reglerna inget annat än fotnoter till definitionen.
recension:
- komponenter i en seriekrets delar samma ström: itotal = I1 = I2 = . . ., I
- är det totala motståndet i en seriekrets lika med summan av de enskilda resistanserna: RTotal = R1 + R2 + . . . Rn
- Total spänning i en seriekrets är lika med summan av de enskilda spänningsfall Etotal = E1 + E2 + . . . Sv
Testa vår Ohms Lagräknare i vår verktygsavdelning.
relaterade kalkylblad:
- serie DC kretsar praktiken kalkylblad med svar kalkylblad
- algebraisk ekvation Manipulation för elektriska kretsar kalkylblad