en sak som vi kommer att göra mycket med algoritmerna i denna serie är graph traversal. Vad betyder det här exakt?
i grund och botten är tanken att vi ska flytta runt grafen från ett vertex till ett annat och upptäcka egenskaperna hos deras sammankopplade relationer.
två av de vanligaste algoritmerna som vi använder mycket är: Depth-First Search (DFS) och Breadth-First Search (BFS).,
medan båda dessa algoritmer tillåter oss att korsa grafer, skiljer de sig på olika sätt. Låt oss börja med DFS.
DFS använder filosofin ”go deep, head first” i genomförandet. Tanken är att från en första vertex (eller plats) går vi ner en väg tills vi når slutet och om vi inte når vår destination kommer vi tillbaka och går ner en annan väg.
låt oss titta på ett exempel., Antag att vi har ett riktat diagram som ser ut så här:

nu är tanken att vi börjar på vertex s och vi blir ombedda att hitta vertex t. med hjälp av DFS kommer vi att utforska en väg, gå hela vägen till slutet och om vi inte hittar t, så går vi ner en annan väg., Här är processen:

Så här går vi nerför vägen (P1) i det första närliggande vertexet och vi ser att det inte är slutet eftersom det har en väg mot ett annat vertex., Så vi går ner den sökvägen:
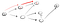
det här är uppenbarligen inte vertex t så vi måste tillbaka för att vi nått en återvändsgränd. Eftersom den tidigare noden inte har längre grannar, går vi tillbaka till s., Från s går vi till sin andra närliggande nod:
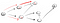
går längs vägen (P2), vi konfronteras med tre grannar., Eftersom den första redan har besökts måste vi gå ner den andra:
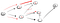
nu, återigen har vi nått en återvändsgränd som inte är vertex t så vi måste gå tillbaka., Eftersom det finns en annan granne som inte har besökts, går vi ner den närliggande sökvägen och äntligen hittade vi vertex t:

Så här fungerar DFS. Gå ner en väg och fortsätt tills du har nått destinationen eller en återvändsgränd. Om det är destinationen, är du klar. Om det inte är, sedan gå tillbaka och fortsätta på en annan väg tills du har uttömt alla alternativ inom den sökvägen.,
Vi kan se att vi följer samma procedur vid varje vertex som vi besöker:
gör en DFS för varje granne i vertex
eftersom detta innebär att du gör samma procedur vid varje steg, berättar något för oss att vi måste använda rekursion för att implementera denna algoritm.
här är koden i JavaScript:
Obs: Denna specifika DFS-algoritm tillåter oss att avgöra om det är möjligt att nå från en plats till en annan., DFS kan användas på olika sätt och det kan finnas subtila förändringar i algoritmen ovan. Det allmänna konceptet är dock detsamma.
analys av DFS
låt oss nu analysera denna algoritm. Eftersom vi går igenom varje granne i noden och vi ignorerar de besökta, har vi en runtime av O(V + E).
en snabb förklaring av exakt vad V+E betyder:
v representerar det totala antalet hörn. E representerar det totala antalet kanter. Varje vertex har ett antal kanter.,
även om det kan tyckas att man kan ledas att tro att det är V * E istället för V + E, låt oss tänka på vad V * E betyder exakt.för att något ska vara V * E, skulle det innebära att för varje vertex måste vi titta på alla kanter i grafen oavsett om dessa kanter är anslutna till det specifika vertexet eller inte.
medan V + E å andra sidan betyder att för varje vertex tittar vi bara på antalet kanter som hänför sig till det vertexet. Minns från föregående inlägg, att det utrymme vi tar upp för adjacency-listan är O (V + E)., Varje vertex har ett antal kanter och i värsta fall, om vi skulle köra DFS på varje vertex, skulle vi ha gjort O(V) arbeta tillsammans med att utforska alla kanter på vertikalerna, vilket är O(E). När vi har tittat på alla v antal hörn, vi skulle också ha tittat på totalt e kanter. Därför är det V + E.
nu, eftersom DFS använder rekursion på varje vertex, betyder det att en stapel används (varför det kallas ett stacköverflödesfel när du stöter på ett oändligt rekursivt samtal). Därför är rymdkomplexiteten O (V).,
nu ska vi se hur bredd-första sökningen skiljer sig.
bredd-första sökningen
bredd-första sökningen (BFS) följer filosofin ”gå bred, fågelperspektiv”. Vad det i grunden betyder är att istället för att gå hela vägen ner en väg till slutet, flyttar BFS mot sin destination en granne i taget., Låt oss titta på vad det betyder:

så istället för att bara gå hela vägen ner sin första granne, skulle BFS besöka alla grannar i s först och sedan besöka dessa grannars grannar och så vidare tills den når t.,fd17d”> 

See how different DFS and BFS behave?, Medan jag gillar att tro att DFS gillar att gå vidare, gillar BFS att se ta det långsamt och observera allt ett steg i taget.
nu ska en fråga som sticker ut för oss vara: ”hur vet vi vilka grannar som ska besöka först från S: S grannar?”
Tja, vi kunde använda en kös första-i-första-ut (FIFO) egendom där vi pop Den första vertex i kön, lägga till sina oönskade grannar i kön, och sedan fortsätta denna process tills kön är antingen tom eller vertex vi lägger till det är vertex vi har letat efter.,låt oss nu titta på koden i JavaScript:
analys av BFS
det kan tyckas att BFS är långsammare. Men om du tittar noga på visualiseringar av både BFS och DFS, hittar du att de faktiskt har samma runtime.
kön ser till att högst varje vertex kommer att behandlas tills den når destinationen. Så det betyder i värsta fall, BFS kommer också att titta på alla hörn och alla kanter.,
medan BFS kan verka långsammare, anses det faktiskt snabbare eftersom om vi skulle implementera dem på större grafer, kommer du att upptäcka att DFS slösar mycket tid på att gå ner långa vägar som i slutändan är fel. Faktum är att BFS ofta används i algoritmer för att bestämma den kortaste vägen från ett vertex till ett annat, men vi kommer att beröra dem senare.
eftersom runtimes är desamma har BFS en runtime av O(V + E) och på grund av användningen av en kö som kan hålla högst V-hörn har den en rymd komplexitet av O (V).,
analogier att lämna bort med
Jag vill lämna dig med andra sätt som jag personligen föreställer mig hur DFS och BFS fungerar i hopp om att det kommer att hjälpa dig att komma ihåg också.
När jag tänker på DFS tycker jag om att tänka på något som hittar rätt väg genom att stöta på många återvändsgränder. Vanligtvis skulle detta vara som en möss som går igenom en labyrint för att leta efter mat.,skulle försöka en sökväg, ta reda på att sökvägen är en återvändsgränd, vrid sedan till en annan sökväg och upprepa denna process tills den når sitt mål:


och det här är vad en förenklad version av processen skulle se ut:

och det här är vad en förenklad version av processen skulle 9781b9b610 ” >
nu för BFS har jag alltid föreställt mig det som en krusning.,div>

ungefär som hur BFS startar vid källan och besöker källans grannar först och sedan går mer utåt genom att besöka sina grannar och så vidare:

sammanfattning
- djup-första sökning (DFS) och bredd-första sökning (BFS) används båda för att korsa grafer.,
- DFS laddar ner en sökväg tills den har uttömt den Sökvägen för att hitta sitt mål, medan BFS krusar genom närliggande hörn för att hitta sitt mål.
- DFS använder en stack medan BFS använder en kö.
- både DFS och BFS har en runtime av O(V + E) och en rymd komplexitet av O(V).
- båda algoritmerna har olika filosofier men har lika stor betydelse för hur vi korsar grafer.