Sannolikhetsfördelning / typer av fördelningar

introduktion

Välkommen till världen av Sannolikhet i datavetenskap! Låt mig börja med ett intuitivt exempel.

anta att du är lärare vid ett universitet. Efter att ha kontrollerat uppdrag i en vecka betygsatte du alla studenter. Du gav dessa graderade papper till en datainmatning kille på universitetet och be honom att skapa ett kalkylblad som innehåller betyg av alla studenter., Men killen lagrar bara betygen och inte motsvarande studenter.

Han gjorde en annan blunder, han missade ett par poster i bråttom och vi har ingen aning om vars betyg saknas. Låt oss hitta ett sätt att lösa detta.

ett sätt är att du visualiserar betygen och ser om du kan hitta en trend i data.

diagrammet som du har plot kallas frekvensfördelningen av data. Du ser att det finns en jämn kurva som struktur som definierar våra data, men märker du en anomali?, Vi har en onormalt låg frekvens vid ett visst poängområde. Så den bästa gissningen skulle vara att ha saknade värden som tar bort bucklan i distributionen.

det här är hur du skulle försöka lösa ett problem i verkligheten med hjälp av dataanalys. För alla Dataforskare, en student eller en utövare, distribution är ett måste vet koncept. Det ger grunden för analys och inferentiell statistik.

medan begreppet Sannolikhet ger oss de matematiska beräkningarna, hjälper distributioner oss att faktiskt visualisera vad som händer under.,

i den här artikeln har jag täckt några viktiga sannolikhetsfördelningar som förklaras på ett tydligt och omfattande sätt.

Obs! den här artikeln förutsätter att du har grundläggande kunskaper om Sannolikhet. Om inte, kan du hänvisa till denna sannolikhetsfördelningar.,

Innehållsförteckning

vanliga datatyper
typer av distributioner
1. Bernoulli Distribution
2. likformig Distribution
3. Binomial Distribution
4. Normal Distribution
5. Poisson Distribution
6. exponentiell Distribution
relationer mellan distributionerna
testa din Distributionsfördelning
kunskap!

vanliga datatyper

innan vi går vidare till förklaringen av distributioner, låt oss se vilken typ av data vi kan stöta på. Data kan vara diskret eller kontinuerlig.,

diskreta Data, som namnet antyder, kan endast ta angivna värden. Till exempel, när du rullar en dö, är de möjliga resultaten 1, 2, 3, 4, 5 eller 6 och inte 1,5 eller 2,45.

kontinuerliga Data kan ta något värde inom ett visst intervall. Intervallet kan vara ändligt eller oändligt. Till exempel en tjejs vikt eller höjd, längden på vägen. Vikten av en tjej kan vara vilket värde som helst från 54 kg, eller 54,5 kg, eller 54.5436 kg.

låt oss nu börja med typerna av distributioner.,

typer av distributioner

Bernoulli Distribution

låt oss börja med den enklaste distributionen som är Bernoulli Distribution. Det är faktiskt lättare att förstå än det låter!

allt du cricket knarkare ute! I början av någon cricket match, Hur bestämmer du vem som ska bat eller boll? En slänga! Det beror på om du vinner eller förlorar kasta, eller hur? Låt oss säga att om kasta resulterar i ett huvud, vinner du. Annars förlorar du. Det finns ingen midway.

en Bernoulli-distribution har bara två möjliga resultat, nämligen 1 (framgång) och 0 (misslyckande) och en enda rättegång., Så den slumpmässiga variabeln X som har en bernoullifördelning kan ta värde 1 med sannolikheten för framgång, säg p och värdet 0 med sannolikheten för misslyckande, säg q eller 1-p.

här betecknar förekomsten av ett huvud framgång, och förekomsten av en svans betecknar misslyckande.
sannolikhet att få ett huvud = 0.5 = sannolikhet att få en svans eftersom det bara finns två möjliga resultat.

sannolikhetsmassfunktionen ges av: px(1-p)1-x där x € (0, 1).,
det kan också skrivas som

sannolikheten för framgång och misslyckande behöver inte vara lika sannolikt, som resultatet av en kamp mellan mig och Undertaker. Han är ganska säker på att vinna. Så i det här fallet är sannolikheten för min framgång 0,15 medan mitt misslyckande är 0,85

här är sannolikheten för framgång (p) inte densamma som sannolikheten för misslyckande. Så diagrammet nedan visar Bernoulli-fördelningen av vår kamp.

här är sannolikheten för framgång = 0,15 och sannolikheten för misslyckande = 0,85., Det förväntade värdet är precis vad det låter. Om jag slår dig, kan jag förvänta mig att du slår mig tillbaka. I grund och botten förväntat värde av någon distribution är medelvärdet av distributionen., Det förväntade värdet av en slumpmässig variabel X från en bernoullifördelning finns enligt följande:

E(X) = 1*p + 0*(1-p) = p

variansen hos en slumpmässig variabel från en bernoullifördelning är:

V(X) = E(X2) – 2 = p – P2 = p(1-p)

det finns många exempel på Bernoulli distribution som om det kommer att regna i morgon eller inte där regn betecknar framgång och inget regn betecknar misslyckande och vinna (framgång) eller förlora (misslyckande) spelet.

enhetlig fördelning

När du rullar en rättvis dö, resultaten är 1 till 6., Sannolikheten för att få dessa resultat är lika sannolikt och det är grunden för en enhetlig fördelning. Till skillnad från Bernoulli Distribution är alla n antal möjliga resultat av en enhetlig fördelning lika troliga.

en variabel X sägs vara jämnt fördelad om densitetsfunktionen är:

grafen för en jämn distributionskurva ser ut som

Du kan se att formen på den enhetliga distributionskurvan är rektangulär, anledningen till att en enhetlig fördelning kallas rektangulär fördelning.,

för en enhetlig fördelning är A och b parametrarna.

antalet buketter som säljs dagligen i en blomsteraffär fördelas jämnt med högst 40 och minst 10.

låt oss försöka beräkna sannolikheten för att den dagliga försäljningen kommer att falla mellan 15 och 30.

sannolikheten att den dagliga försäljningen kommer att falla mellan 15 och 30 är (30-15)*(1/(40-10)) = 0.5

på samma sätt är sannolikheten att den dagliga försäljningen är större än 20 = 0.,667

medelvärdet och variansen för X efter en enhetlig fördelning är:

medelvärde -> E(X) = (A+b)/2

varians -> V(X) = (b-a)2/12

standard enhetlig densitet har parametrar a = 0 och b = 1, Så PDF för standard enhetlig densitet är ges av:

binomial distribution

låt oss komma tillbaka till cricket. Antag att du vann kasta idag och detta indikerar en lyckad händelse. Du kastar igen, men du förlorade den här gången., Om du vinner en kasta idag, detta inte nödvändiggör att du kommer att vinna kasta i morgon. Låt oss tilldela en slumpmässig variabel, säg X, till antalet gånger du vann kasta. Vad kan vara det möjliga värdet av X? Det kan vara vilket nummer som helst beroende på antalet gånger du kastade ett mynt.

det finns bara två möjliga resultat. Huvud betecknar framgång och svans betecknar misslyckande. Därför kan sannolikheten för att få ett huvud = 0,5 och sannolikheten för misslyckande lätt beräknas som: q = 1 – p = 0,5.,

en fördelning där endast två resultat är möjliga, såsom framgång eller misslyckande, vinst eller förlust, vinna eller förlora och där sannolikheten för framgång och misslyckande är densamma för alla försök kallas en binomialfördelning.

resultaten behöver inte vara lika troliga. Minns du ett exempel på en kamp mellan mig och begravningsentreprenören? Så, om sannolikheten för framgång i ett experiment är 0,2, kan sannolikheten för misslyckande enkelt beräknas som q = 1-0,2 = 0,8.

varje försök är oberoende eftersom resultatet av den tidigare kasta inte bestämma eller påverka resultatet av den nuvarande kasta., Ett experiment med endast två möjliga resultat upprepas n antal gånger kallas binomial. Parametrarna för en binomialfördelning är n och p där n är det totala antalet försök och p är sannolikheten för framgång i varje försök.

på grundval av ovanstående förklaring är egenskaperna hos en binomialfördelning

varje försök är oberoende.
Det finns bara två möjliga resultat i en rättegång – antingen en framgång eller ett misslyckande.
ett totalt antal n identiska försök utförs.
sannolikheten för framgång och misslyckande är densamma för alla försök., (Försök är identiska.,

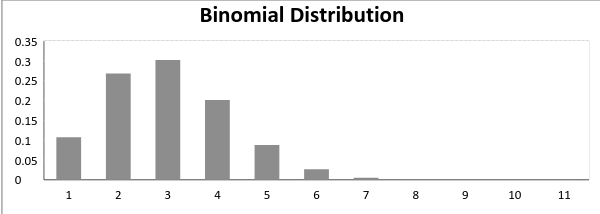
nu, när sannolikheten för framgång = Sannolikhet för misslyckande, i en sådan situation ser grafen för binomialfördelning ut

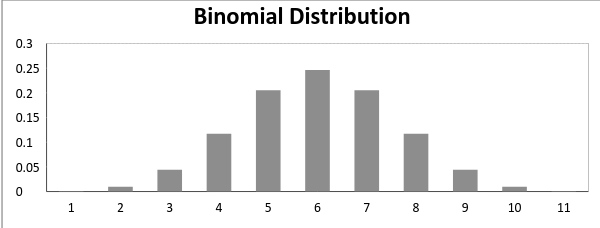
medelvärdet och variansen för en binomialfördelning ges av:

medelvärde –

div id=”aca2d19001″>µ = n*p

varians- > var(x) = n*p*q

normal distribution

normal distribution representerar beteendet hos de flesta situationer i universum (det är därför det kallas en ”normal” distribution., Antar jag!). Den stora summan av (små) slumpmässiga variabler visar sig ofta vara normalt fördelad, vilket bidrar till dess utbredda tillämpning. All distribution kallas Normal distribution om den har följande egenskaper:
1. medelvärdet, medianen och läget för distributionen sammanfaller.
2. distributionskurvan är klockformad och symmetrisk om linjen x=μ.
3. den totala ytan under kurvan är 1.
4. exakt hälften av värdena är till vänster om mitten och den andra hälften till höger.,
en normal fördelning skiljer sig mycket från binomialfördelningen. Men om antalet försök närmar sig oändligheten kommer formerna att vara ganska lika.

PDF-filen för en slumpmässig variabel X efter en normal fördelning ges av:

medelvärdet och variansen för en slumpmässig variabel X som sägs vara normalt distribuerad ges av:

medelvärde- > E(X) = µ

varians – > var(X) = σ^2

här är µ (medelvärde) och σ (standardavvikelse) parametrarna.,
diagrammet för en slumpmässig variabel X ~ N (µ, σ) visas nedan.

en standard normalfördelning definieras som fördelningen med medelvärde 0 och standardavvikelse 1. För ett sådant fall blir PDF:

Poisson Distribution

Antag att du arbetar på ett callcenter, ungefär hur många samtal får du på en dag? Det kan vara vilket nummer som helst. Nu är hela antalet samtal på ett callcenter på en dag modellerad av Poisson distribution., Några fler exempel är
1. antalet nödsamtal som registrerats på ett sjukhus på en dag.
2. antalet stölder som rapporteras i ett område på en dag.
3. antalet kunder som anländer till en salong på en timme.
4. antalet självmord som rapporterats i en viss stad.
5. antalet utskriftsfel på varje sida i boken.
Du kan nu tänka på många exempel efter samma kurs., Poisson Distribution är tillämplig i situationer där händelser inträffar vid slumpmässiga tidpunkter och rum där vårt intresse ligger endast i antalet händelser av händelsen.

en distribution kallas Poisson distribution när följande antaganden är giltiga:

1. Varje lyckad händelse bör inte påverka resultatet av en annan framgångsrik händelse.
2. Sannolikheten för framgång över ett kort intervall måste motsvara sannolikheten för framgång över ett längre intervall.
3. Sannolikheten för framgång i ett intervall närmar sig noll eftersom intervallet blir mindre.,

om någon distribution validerar ovanstående antaganden är det en Poisson-distribution. Vissa noteringar som används i Poisson-distributionen är:
- λ är den takt med vilken en händelse inträffar,
- t är längden på ett tidsintervall,
- och X är antalet händelser i det tidsintervallet.
här kallas X en Poisson slumpvariabel och sannolikhetsfördelningen för X kallas Poisson distribution.

låt µ beteckna medelantalet händelser i ett längdintervall t.därefter µ = λ*t.,

PMF för X efter en Poisson-distribution ges av:

medelvärdet µ är parametern för denna distribution. µ definieras också som λ – tidslängden för det intervallet. Diagrammet för en Poisson-distribution visas nedan:

diagrammet som visas nedan visar kurvskiftet på grund av ökning av medelvärdet.

det är märkbart att kurvan skiftar åt höger när medelvärdet ökar.,

medelvärdet och variansen för X efter en Poisson-distribution:

medelvärde- > E(X) = µ
varians – > Var(X) = µ

exponentiell Distribution

låt oss överväga call center-exemplet en gång till. Hur är det med tidsintervallet mellan samtalen ? Här kommer exponentiell distribution till vår räddning. Exponentiell distributionsmodeller tidsintervallet mellan samtalen.

andra exempel är:

1. Tid beteeen metro ankomster,
2., Tidslängd mellan ankomster vid en bensinstation
3. Livslängden hos en luftkonditionering

exponentiell distribution används ofta för överlevnadsanalys. Från den förväntade livslängden för en maskin till den förväntade livslängden för en människa, exponentiell distribution levererar framgångsrikt resultatet.

en slumpmässig variabel X sägs ha en exponentiell distribution med PDF:

f(x) = { λe-λx, x ≥ 0

och parameter λ>0 som också kallas räntan.,

för överlevnadsanalys kallas λ felfrekvensen för en enhet när som helst t, eftersom den har överlevt upp till t.

medelvärde och varians för en slumpmässig variabel X efter en exponentiell fördelning:

medelvärde -> E(X) = 1/λ

varians -> var(x) = (1/λ)2

ju större hastigheten desto snabbare kurvan sjunker och ju lägre hastigheten, smickrar kurvan. Detta förklaras bättre med diagrammet nedan.,

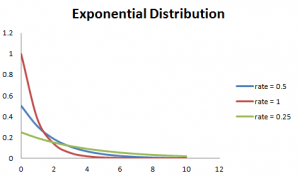
för att underlätta beräkningen finns det några formler som anges nedan.
p{x≤x} = 1 – e-λx, motsvarar området under densitetskurvan till vänster om x.

P{X>x} = e-λx, motsvarar området under densitetskurvan till höger om x.

p{x1<x≤ x2} = e-λx1 – e-λx2, motsvarar området under densitetskurvan till höger om x.

p {x1 < x ≤ x2} = e-λx1-e-λx2, motsvarar området under Densitetskurvan mellan X1 och X2.

förhållandet mellan distributionerna

förhållandet mellan Bernoulli och Binomial Distribution

1., Bernoulli Distribution är ett speciellt fall av Binomial Distribution med en enda rättegång.

2. Det finns bara två möjliga resultat av en Bernoulli och Binomial distribution, nämligen framgång och misslyckande.

3. Både Bernoulli och Binomialfördelningar har oberoende spår.

förhållandet mellan Poisson och Binomial Distribution

Poisson Distribution är ett begränsande fall av binomial distribution under följande villkor:
1. antalet försök är obestämt stor eller n→.,
2. sannolikheten för framgång för varje försök är densamma och obestämd tid liten eller p →0.
3. NP = λ, är ändlig.
förhållandet mellan Normal och Binomial Distribution& Normal och Poisson Distribution:

Normal distribution är en annan begränsande form av binomial distribution under följande villkor:
1. antalet försök är obestämt stor, n →
2. både p och q är inte obestämt små.
den normala fördelningen är också ett begränsande fall av Poisson-fördelning med parametern λ→.,

Relation mellan exponentiell och Poisson fördelning:

om tiderna mellan slumpmässiga händelser följer exponentiell fördelning med hastighet λ, då det totala antalet händelser i en tidsperiod av längd T följer Poisson fördelning med parameter λt.

testa dina kunskaper

Du har kommit så här långt. Kan du svara på följande frågor? Låt mig veta i kommentarerna nedan!

1. Formeln för att beräkna standard normal slumpvariabel är:

A. (x + µ) / σ
b. (x-µ) / σ
c. (x-σ)/µ

2., I Bernoulli-fördelningen ges formeln för beräkning av standardavvikelse av:

a. p (1 – p)
b. SQRT(p(p – 1))
C. SQRT(p (1 – p))

3. För en normal fördelning kommer en ökning av medelvärdet:

a. Skift kurvan till vänster
b. Skift kurvan till höger
C.platta kurvan

4. Batteriets livslängd fördelas exponentiellt med λ = 0,05 per timme. Sannolikheten för att ett batteri ska vara mellan 10 och 15 timmar är:

a. 0. 1341
b.0.1540
c.0.,0079

slutnot

sannolikhetsfördelningar är vanliga inom många sektorer, nämligen försäkring, fysik, teknik, datavetenskap och till och med samhällsvetenskap, där studenterna i psykologi och medicinsk använder ofta sannolikhetsfördelningar. Den har en enkel applikation och utbredd användning. Denna artikel belyste sex viktiga fördelningar som observeras i det dagliga livet och förklarade deras tillämpning. Nu kommer du att kunna identifiera, relatera och skilja mellan dessa distributioner.,

om du har några tvivel och vill se fler artiklar om distributioner, skriv gärna i kommentarfältet nedan. För en mer djupgående skrivning av dessa distributioner kan du referera till den här resursen.