un lucru pe care îl vom face foarte mult cu algoritmii din această serie este traversarea graficului. Ce înseamnă asta mai exact?
practic, ideea este că ne vom deplasa în jurul graficului de la un vârf la altul și vom descoperi proprietățile relațiilor lor interconectate.doi dintre cei mai folosiți algoritmi pe care îi vom folosi foarte mult sunt: Depth-First Search (DFS) și width-First Search (BFS).,în timp ce ambii algoritmi ne permit să traversăm grafice, acestea diferă în moduri diferite. Să începem cu DFS.DFS utilizează filozofia „go deep, head first” în implementarea sa. Ideea este că pornind de la un vârf (sau loc) inițial, mergem pe o cale până ajungem la sfârșit și dacă nu ajungem la destinație, atunci ne întoarcem și mergem pe o altă cale.
să ne uităm la un exemplu., Să presupunem că avem un graf orientat care arata ca aceasta:

Acum ideea este că vom începe de la vârful s și ne-a cerut să găsească nod t. Folosind DFS, vom explora o cale, du-te tot drumul până la capăt și dacă nu vom găsi t, apoi vom merge pe o altă cale., Aici este procesul de:

Deci, aici vom merge pe calea (p1) de la primul vecine vertex și vom vedea că acesta nu este sfârșitul, deoarece are o cale spre un alt nod., Deci, vom merge pe aceasta cale:
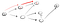
Acest lucru este în mod clar nu vertex t deci trebuie să mă întorc pentru că am ajuns la un dead end. Deoarece nodul anterior nu mai are vecini, ne întoarcem la s., La s, mergem la a doua vecine nod:
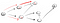
Mergând pe calea (p2), ne-am confruntat cu trei vecini., Deoarece primul a fost deja vizitat, trebuie să mergem în jos cel de-al doilea:
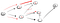
Acum, încă o dată am ajuns la o fundătură care nu este nod t așa că trebuie să mergem înapoi., Deoarece nu există un alt vecin care nu a fost vizitat, vom merge în jos că vecine calea și în sfârșit am găsit nodul t:

Acesta este modul în DFS funcționează. Du-te în jos o cale și să păstreze merge până când ați ajuns la destinație sau o fundătură. Dacă este destinația, ați terminat. Dacă nu, atunci mergeți înapoi și continuați pe o altă cale până când ați epuizat toate opțiunile din acea cale.,
putem vedea că Avem urmați aceeași procedură la fiecare nod care vom vizita:
Fac un DFS pentru fiecare vecin al nodului
Deoarece aceasta presupune a face aceeași procedură la fiecare pas, ceva ne spune că avem nevoie de a utiliza recursivitate pentru a implementa acest algoritm.
Aici este codul JavaScript:
Notă: Această specific DFS algoritm ne permite pentru a determina dacă este posibil să se ajungă la un loc la altul., DFS pot fi utilizate într-o varietate de moduri și pot exista modificări subtile la algoritmul de mai sus. Cu toate acestea, conceptul general rămâne același.
analiza DFS
acum să analizăm acest algoritm. Deoarece traversăm fiecare vecin al nodului și ignorăm cele vizitate, avem un timp de rulare de O(V + e).
o explicație rapidă a exact ceea ce înseamnă V+e:
V reprezintă numărul total de noduri. E reprezintă numărul total de margini. Fiecare nod are un număr de margini.,
deși poate părea că cineva poate fi condus să creadă că este V•e în loc de V + e, să ne gândim la ce înseamnă exact V•E.pentru ca ceva sa fie V * E, ar insemna ca pentru fiecare nod, trebuie sa ne uitam la toate marginile din grafic indiferent daca acele margini sunt sau nu conectate la acel nod specific.
In timp ce, pe de alta parte, V + e inseamna ca pentru fiecare nod, ne uitam doar la numarul de muchii care se refera la acel nod. Reamintim din postul anterior, că spațiul pe care îl luăm pentru lista de adiacență este O(V + e)., Fiecare nod are un număr de muchii și în cel mai rău caz, dacă ar fi să rulăm DFS pe fiecare nod, am fi lucrat O(V) împreună cu explorarea tuturor marginilor vârfurilor, care este O(E). Odată ce ne-am uitat la toate V numărul de noduri, ne-ar fi uitat, de asemenea, la un total de e margini. Prin urmare, este V + E.
acum, deoarece DFS folosește recursivitatea pe fiecare nod, asta înseamnă că se folosește o stivă (de aceea se numește o eroare de depășire a stivei ori de câte ori executați un apel recursiv infinit). Prin urmare, complexitatea spațiului este O(V).,acum, să vedem cum diferă lățimea – prima căutare.
lățime-prima căutare
lățime-prima căutare (BFS) urmează filosofia „go wide, bird ‘ s eye-view”. Ceea ce înseamnă practic este că, în loc să meargă până la capăt pe o cale până la sfârșit, BFS se îndreaptă spre destinație un vecin la un moment dat., Să ne uităm la ce înseamnă asta:

Deci, în loc de a merge tot drumul în jos primul său vecin, BFS-ar vizita toți vecinii de primul și apoi vizita celor vecinilor vecinii și așa mai departe până când se ajunge la t.,fd17d”> 

See how different DFS and BFS behave?, În timp ce îmi place să cred că DFS îi place să meargă pe cap, BFS îi place să se uite ia-o încet și să observe totul un pas la un moment dat.acum, o întrebare care ne iese în evidență ar trebui să fie: „cum știm care vecini să viziteze mai întâi de la vecinii lui s?”
Ei bine, am putea utiliza proprietatea first-in-first-out (FIFO) a unei cozi unde deschidem primul nod al cozii, adăugăm vecinii nevizitați la coadă și apoi continuăm acest proces până când coada este fie goală, fie nodul pe care îl adăugăm este vârful pe care l-am căutat.,
Acum să ne uităm la cod în JavaScript:
Analiza BFS
poate părea BFS este mai lent. Dar dacă te uiți cu atenție la vizualizările atât ale BFS, cât și ale DFS, vei descoperi că au de fapt același timp de rulare.
coada asigură că cel mult fiecare nod va fi procesat până când ajunge la destinație. Deci, asta înseamnă că, în cel mai rău caz, BFS va analiza, de asemenea, toate vârfurile și toate marginile.,
în timp ce BFS poate părea mai lent, este de fapt considerat mai rapid, deoarece dacă ar fi să le implementăm pe grafice mai mari, veți descoperi că DFS pierde mult timp mergând pe căi lungi care sunt în cele din urmă greșite. De fapt, BFS este adesea folosit în algoritmi pentru a determina calea cea mai scurtă de la un nod la altul, dar le vom atinge mai târziu.deci, din moment ce runtime-urile sunt aceleași, BFS are o runtime de O(V + E) și datorită utilizării unei cozi care poate ține cel mult v noduri, are o complexitate de spațiu de O(V).,
analogii pentru a pleca cu
vreau să vă las cu alte moduri în care îmi imaginez personal cum funcționează DFS și BFS în speranța că vă va ajuta să vă amintiți și voi.ori de câte ori mă gândesc la DFS, îmi place să mă gândesc la ceva care găsește calea cea bună prin lovirea într-o mulțime de fundături. De obicei, acest lucru ar fi ca un soareci trece printr-un labirint pentru a căuta hrană.,ar încerca o cale, pentru a afla că drumul este într-o fundătură, atunci pivot pentru o altă cale și repetați acest proces până când ajunge la țintă:

Și aceasta este ceea ce o versiune simplificată a procesului ar arăta astfel:

Acum, pentru BFS, Mereu mi-am imaginat ca o unda.,div>

la fel ca modul în BFS începe de la sursă și vizite sursa vecinii lui mai întâi și apoi se duce mai mult spre exterior prin vizitarea lor, vecinii și așa mai departe:

Rezumat
- Depth-First Search (DFS) și Lățimea în Primul rând de Căutare (BFS) sunt ambele utilizate pentru a traversa grafice.,
- DFS se încarcă pe o cale până când a epuizat acea cale pentru a-și găsi ținta, în timp ce BFS se învârte prin vârfurile vecine pentru a-și găsi ținta.
- DFS utilizează o stivă în timp ce BFS utilizează o coadă.
- ambele DFS și BFS au o runtime de O(V + E) și o complexitate spațiu de O (V).
- ambii algoritmi au filozofii diferite, dar au o importanță egală în modul în care traversăm graficele.