Distribuția probabilității / tipuri de distribuții

Introducere

Bine ați venit în lumea probabilității în știința datelor! Permiteți-mi să încep lucrurile cu un exemplu intuitiv.să presupunem că sunteți profesor la o universitate. După ce ați verificat sarcinile timp de o săptămână, ați evaluat toți studenții. I-ai dat aceste note unui tip din universitate și i-ai spus să creeze o foaie de calcul care să conțină notele tuturor studenților., Dar tipul stochează doar notele și nu studenții corespunzători.

a făcut o altă gafă, a ratat câteva intrări în grabă și nu avem idee ale căror note lipsesc. Să găsim o cale să rezolvăm asta.

o modalitate este să vizualizați notele și să vedeți dacă puteți găsi o tendință în date.

graficul pe care îl aveți complot se numește distribuția frecvenței datelor. Vedeți că există o curbă netedă ca structura care definește datele noastre, dar observați o anomalie?, Avem o frecvență anormal de scăzută la un anumit interval de scor. Deci, cea mai bună presupunere ar fi să existe valori lipsă care să elimine dentul din distribuție.

acesta este modul în care ați încerca să rezolvați o problemă din viața reală folosind analiza datelor. Pentru orice om de știință de date, student sau practicant, distribuția este un concept trebuie să știe. Acesta oferă baza pentru analiză și statistici inferențiale.

în timp ce conceptul de probabilitate ne oferă calculele matematice, distribuțiile ne ajută să vizualizăm de fapt ce se întâmplă dedesubt.,în acest articol, am acoperit câteva distribuții importante de probabilitate care sunt explicate într-un mod lucid și cuprinzător.Notă: Acest articol presupune că aveți cunoștințe de bază despre probabilitate. Dacă nu, puteți referi aceste distribuții de probabilitate.,

Cuprins

Tipuri de Date Comune
Tipuri de Distribuții
1. Distribuția Bernoulli
2. Distribuția Uniformă
3. Distribuția Binomială
4. Distribuția Normală
5. Distribuția Poisson
6. Distribuția Exponențială
Relațiile dintre Distribuțiile
Testați-vă Cunoștințele!

tipuri comune de date

înainte de a trece la explicația distribuțiilor, să vedem ce fel de date putem întâlni. Datele pot fi discrete sau continue.,

datele Discrete, după cum sugerează și numele, pot lua numai valori specificate. De exemplu, atunci când rola o matriță, rezultatele posibile sunt 1, 2, 3, 4, 5 sau 6 și nu 1.5 sau 2.45.

datele continue pot lua orice valoare într-un anumit interval. Intervalul poate fi finit sau infinit. De exemplu, greutatea sau înălțimea unei fete, lungimea drumului. Greutatea unei fete poate fi orice valoare de la 54 kg sau 54,5 kg sau 54,5436 kg.acum să începem cu tipurile de distribuții.,

tipuri de distribuții

distribuția Bernoulli

Să începem cu cea mai ușoară distribuție care este distribuția Bernoulli. Este de fapt mai ușor de înțeles decât pare!

toți drogații de cricket acolo! La începutul oricărui meci de cricket, cum decideți cine va bate sau mingea? O aruncare! Totul depinde dacă câștigi sau pierzi aruncarea, nu? Să spunem că dacă aruncarea are ca rezultat un cap, câștigi. Altfel, ai pierdut. Nu e nici un mijloc.o distribuție Bernoulli are doar două rezultate posibile, și anume 1 (succes) și 0 (eșec), și un singur proces., Deci variabila aleatorie X care are o distribuție Bernoulli poate lua valoarea 1 cu probabilitatea de succes, să zicem p, iar valoarea 0 cu probabilitatea de eșec, să zicem q sau 1-p.

aici, apariția unui cap denotă succes, iar apariția unei coadă denotă eșec.
probabilitatea de a obține un cap = 0,5 = probabilitatea de a obține o coadă, deoarece există doar două rezultate posibile.

funcția de masă de probabilitate este dată de: px(1-p)1-x unde x € (0, 1).,
acesta poate fi, de asemenea, scris ca

probabilitățile de succes și eșec nu trebuie să fie la fel de probabil, ca rezultatul unei lupte între Mine și Undertaker. E destul de sigur că va câștiga. Deci, în acest caz, probabilitatea succesului meu este 0.15 în timp ce eșecul meu este 0.85

aici, probabilitatea de succes(p) nu este aceeași cu probabilitatea de eșec. Deci, graficul de mai jos arată distribuția Bernoulli a luptei noastre.

aici, probabilitatea de succes = 0,15 și probabilitatea de eșec = 0,85., Valoarea așteptată este exact ceea ce sună. Dacă te pocnesc, mă aștept să mă pocnești și tu. Practic, valoarea așteptată a oricărei distribuții este media distribuției., Valoarea așteptată a unei variabile aleatoare X de la un Bernoulli distribuție este de găsit, după cum urmează:

E(X) = 1*p + 0*(1-p) = p

varianța unei variabile aleatoare din distribuția bernoulli este:

V(X) = E(X2) – 2 = p – p2 = p(1-p)

Există multe exemple de Bernoulli distribuție cum ar fi dacă o să plouă mâine sau nu în cazul în care ploaia denotă succesul și nici o ploaie denotă eșecul și de a Câștiga (succes) sau pierderea (lipsa) de joc.

distribuție uniformă

când rotiți o matriță corectă, rezultatele sunt de la 1 la 6., Probabilitățile de a obține aceste rezultate sunt la fel de probabile și aceasta este baza unei distribuții uniforme. Spre deosebire de distribuția Bernoulli, toate n numărul de rezultate posibile ale unei distribuții uniforme sunt la fel de probabil.

O variabilă X este declarat a fi uniform distribuite, dacă funcția de densitate este:

grafic de o distribuție uniformă a curbei se pare că

puteți vedea că forma de distribuție Uniformă a curbei este dreptunghiular, motivul pentru distribuirea Uniformă se numește distribuție dreptunghiulară.,pentru o distribuție uniformă, a și b sunt parametrii. numărul de buchete vândute zilnic la o florărie este distribuit uniform cu un maxim de 40 și un minim de 10.să încercăm să calculăm probabilitatea ca vânzările zilnice să scadă între 15 și 30.probabilitatea ca vânzările zilnice să scadă între 15 și 30 este (30-15)*(1/(40-10)) = 0.5în mod similar, probabilitatea ca vânzările zilnice să fie mai mari de 20 este = 0.,667

media și varianța X urmărind o distribuție uniformă este:

Adică> E(X) = (a+b)/2

Varianță -> V(X) = (b-a)2/12

standard densitate uniformă a parametrilor a = 0 și b = 1, deci PDF pentru standard densitate uniformă este dat de:

Distribuția Binomială

să ne întoarcem la cricket. Să presupunem că ați câștigat aruncarea astăzi și acest lucru indică un eveniment de succes. Arunci din nou, dar ai pierdut de data asta., Dacă veți câștiga o aruncare astăzi, acest lucru nu necesită că va câștiga mâine aruncare. Să atribuim o variabilă aleatorie, Să zicem X, numărului de ori în care ați câștigat aruncarea. Care poate fi valoarea posibilă a lui X? Acesta poate fi orice număr, în funcție de numărul de ori ai aruncat o monedă.există doar două rezultate posibile. Capul care denotă succesul și coada care denotă eșecul. Prin urmare, probabilitatea de a obține un cap = 0,5 și probabilitatea de eșec poate fi ușor calculată ca: q = 1 – p = 0,5.,o distribuție în care sunt posibile doar două rezultate, cum ar fi succesul sau eșecul, câștigul sau pierderea, câștigul sau pierderea și unde probabilitatea de succes și eșec este aceeași pentru toate studiile se numește distribuție binomială.rezultatele nu trebuie să fie la fel de probabile. Îți amintești exemplul unei lupte între Mine și Undertaker? Deci, dacă probabilitatea de succes într – un experiment este de 0,2, atunci probabilitatea de eșec poate fi ușor calculată ca q = 1-0,2 = 0,8.fiecare încercare este independentă, deoarece rezultatul aruncării anterioare nu determină sau nu afectează rezultatul aruncării curente., Un experiment cu doar două rezultate posibile repetate n număr de ori se numește binom. Parametrii unei distribuții binomiale sunt n și p unde n este numărul total de încercări și p este probabilitatea de succes în fiecare proces.pe baza explicației de mai sus, proprietățile unei distribuții binomiale sunt

fiecare proces este independent.
există doar două rezultate posibile într – un proces-fie un succes, fie un eșec.
un număr total de n studii identice sunt efectuate.
probabilitatea de succes și eșec este aceeași pentru toate încercările., (Studiile sunt identice.,

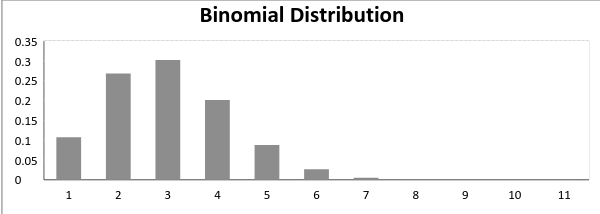
Acum, când probabilitatea de succes = probabilitatea de eșec, într-o asemenea situație graficul de distribuție binomială se pare că

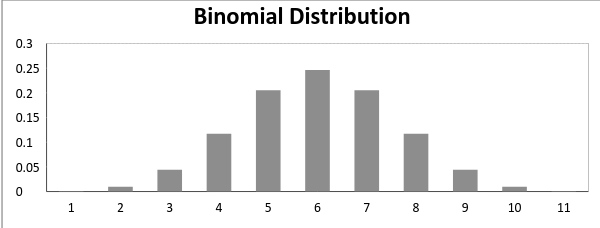
media și varianța unei distribuții binomiale sunt date de:

Adică> µ = n*p

Varianță -> Var(X) = n*p*q

Distribuție Normală

distribuția Normală reprezintă comportamentul celor mai multe dintre situațiile în univers (de Aceea se numește „normal” de distribuție., Cred!). Suma mare de variabile aleatoare (mici) se dovedește adesea distribuită în mod normal, contribuind la aplicarea sa pe scară largă. Orice distribuție este cunoscută ca distribuție normală dacă are următoarele caracteristici:
1. media, mediana și modul de distribuție coincid.
2. curba distribuției este în formă de clopot și simetrică în jurul liniei x = μ.
3. suprafața totală de sub curbă este 1.
4. exact jumătate din valori sunt la stânga centrului și cealaltă jumătate la dreapta.,
o distribuție normală este foarte diferită de distribuția binomială. Cu toate acestea, dacă numărul de încercări se apropie de infinit, atunci formele vor fi destul de similare.

PDF a unei variabile aleatoare X în urma o distribuție normală este dată de:

media și varianța unei variabile aleatoare X care este declarat a fi, în mod normal, distribuite este dat de:

Adică> E(X) = µ

Varianță -> Var(X) = σ^2

Aici, µ (medie) și σ (abaterea standard) sunt parametrii.,
graficul unei variabile aleatorii X ~ N (µ, σ) este prezentat mai jos.

o distribuție normală standard este definită ca distribuția cu media 0 și deviația standard 1. Pentru un astfel de caz, PDF devine:

Distribuția Poisson

să Presupunem că lucra la un call center, aproximativ cât de multe apeluri puteți obține într-o zi? Poate fi orice număr. Acum, întregul număr de apeluri la un centru de apel într-o zi este modelat de Poisson distribution., Câteva exemple sunt
1. numărul de apeluri de urgență înregistrate la un spital într-o zi.
2. numărul de furturi raportate într-o zonă într-o zi.
3. numărul de clienți care sosesc la un salon într-o oră.
4. numărul de sinucideri raportate într-un anumit oraș.
5. numărul de erori de imprimare la fiecare pagină a cărții.
acum vă puteți gândi la multe exemple urmând același curs., Distribuția Poisson este aplicabilă în situațiile în care evenimentele au loc în momente aleatorii de timp și spațiu în care interesul nostru se află numai în numărul de evenimente ale evenimentului.o distribuție se numește distribuție Poisson atunci când sunt valabile următoarele ipoteze:

1. Orice eveniment de succes nu ar trebui să influențeze rezultatul unui alt eveniment de succes.
2. Probabilitatea de succes într-un interval scurt trebuie să fie egală cu probabilitatea de succes într-un interval mai lung.
3. Probabilitatea de succes într-un interval se apropie de zero, deoarece intervalul devine mai mic.,acum, dacă orice distribuție validează ipotezele de mai sus, atunci este o distribuție Poisson. Unele notații utilizate în distribuția Poisson sunt:
- λ este rata la care are loc un eveniment,
- t este lungimea unui interval de timp,
- și X este numărul de evenimente din acel interval de timp.aici, X se numește variabilă aleatorie Poisson, iar distribuția probabilității lui X se numește distribuție Poisson.
  fie µ să desemneze numărul mediu de evenimente într-un interval de lungime t. apoi, µ = λ*t.,
  
  PMF-ul lui X după o distribuție Poisson este dat de:
  
  media µ este parametrul acestei distribuții. µ este, de asemenea, definit ca λ ori lungimea acestui interval. Graficul unei distribuții Poisson este prezentat mai jos:
  
  graficul prezentat mai jos ilustrează schimbarea curbei datorită creșterii mediei.
  
  Acesta este perceptibil ca medie crește, curba se deplasează spre dreapta.,
  
  media și varianța lui X după o distribuție Poisson:
  
  Adică> E(X) = µ
  Varianță -> Var(X) = µ
  
  Distribuția Exponențială
  
  Să ia în considerare call center exemplu, unul mai mult timp. Cum rămâne cu intervalul de timp dintre apeluri ? Aici, distribuția exponențială vine în ajutorul nostru. Distribuția exponențială modelează intervalul de timp dintre apeluri.alte exemple sunt:
  
  1. Durata de timp beteeen metro sosiri,
  2., Durata de timp între sosiri la o benzinărie
  3. Durata de viață a unui aparat de aer condiționat
  
  distribuția exponențială este utilizată pe scară largă pentru analiza supraviețuirii. De la viața așteptată a unei mașini la viața așteptată a unui om, distribuția exponențială oferă cu succes rezultatul.
  
  O variabilă aleatoare X este declarat de a avea o distribuție exponențială cu PDF:
  
  f(x) = { λe-λx, x ≥ 0
  
  și parametrul λ>0, care este, de asemenea, numit rata.,
  
  Pentru analiza de supraviețuire, λ se numește rata de eșec a unui dispozitiv, în orice moment t, având în vedere că acesta a supraviețuit până la t.
  
  media și Varianța unei variabile aleatoare X, în urma unei distribuția exponențială:
  
  Adică> E(X) = 1/λ
  
  Varianță -> Var(X) = (1/λ)2
  
  de Asemenea, cea mai mare rata, cu atât mai repede curba scade și cea mai mică rată, flata curba. Acest lucru este explicat mai bine cu graficul prezentat mai jos.,
  
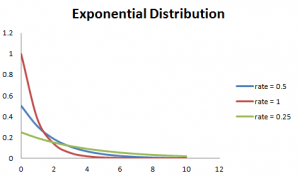
  pentru a ușura calculul, există câteva formule prezentate mai jos.
  P{X≤x} = 1 – e-λx, corespunde cu aria de sub densitatea curbă la stânga lui x.
  
  P{X>x} = e-λx, corespunde cu aria de sub densitatea curbă la dreapta a lui x.
  
  P{x1<X≤ x2} = e-λx1 – e-λx2, corespunde ariei de sub curba de densitate între x1 și x2.
  
  relațiile dintre distribuții
  
  relația dintre Bernoulli și distribuția binomială
  
  1., Distribuția Bernoulli este un caz special de distribuție binomială cu un singur proces.
  
  2. Există doar două rezultate posibile ale unei distribuții Bernoulli și binomiale, și anume Succesul și eșecul.
  
  3. Atât distribuțiile Bernoulli, cât și cele binomiale au trasee independente.
  
  relația dintre Poisson și distribuția binomială
  
  distribuția Poisson este un caz limitativ de distribuție binomială în următoarele condiții:
  1. numărul de studii este nedefinit mare sau n → ∞.,
  2. probabilitatea de succes pentru fiecare proces este aceeași și pe termen nelimitat mic sau p →0.
  3. np = λ, este finit.
  Relația dintre Normal și Distribuție Binomială & Normală și Distribuția Poisson:
  
  distribuția Normală este o altă limitare formă de distribuție binomială în următoarele condiții:
  1. numărul de încercări este nesfârșit de mare, n → ∞.
  2. atât p cât și q nu sunt la nesfârșit mici.distribuția normală este, de asemenea, un caz limitativ al distribuției Poisson cu parametrul λ →∞.,
    
    Relația dintre Exponențială și Distribuția Poisson:
    
    Dacă ori între evenimente aleatoare urmează distribuția exponențială cu rata λ, atunci numărul total de evenimente într-o perioadă de timp de lungime t urmează distribuția Poisson cu parametrul λt.
    
    Testați-vă cunoștințele
    
    ați ajuns atât de departe. Acum, sunteți în măsură să răspundă la următoarele întrebări? Lasă-mă să știu în comentariile de mai jos!
    
    1. Formula pentru a calcula variabila aleatoare normală standard este:
    
    a. (x + µ) / σ
    b. (x-µ) / σ
    c. (x-σ) / µ
    
    2., În distribuția Bernoulli, formula pentru calcularea deviației standard este dată de:
    
    a. P (1-p)
    b. SQRT(p(p – 1))
    c. SQRT(p(1 – p))
    
    3. Pentru o distribuție normală, o creștere a mediei va:
    
    a. deplasați curba spre stânga
    b. deplasați curba spre dreapta
    c. aplatizați curba
    
    4. Durata de viață a unei baterii este distribuită exponențial cu λ = 0,05 pe oră. Probabilitatea pentru o baterie să dureze între 10 și 15 ore este:
    
    un.0.1341
    b.0.1540
    c.0.,0079
    
    End note
    
    distribuții de probabilitate sunt predominante în multe sectoare, și anume, asigurări, fizică, inginerie, informatică și chiar științe Sociale în care studenții de Psihologie și medicale sunt pe scară largă folosind distribuții de probabilitate. Are o aplicație ușoară și o utilizare pe scară largă. Acest articol a evidențiat șase distribuții importante care sunt observate în viața de zi cu zi și a explicat aplicarea lor. Acum veți putea identifica, relaționa și diferenția între aceste distribuții.,dacă aveți îndoieli și doriți să vedeți mai multe articole despre distribuții, vă rugăm să scrieți în secțiunea de comentarii de mai jos. Pentru o scriere mai aprofundată a acestor distribuții, puteți consulta această resursă.