jedną z rzeczy, które będziemy robić wiele z algorytmami z tej serii jest graph traversal. Co to dokładnie oznacza?
zasadniczo chodzi o to, że będziemy poruszać się po grafie z jednego wierzchołka do drugiego i odkrywać właściwości ich powiązanych relacji.
dwa z najczęściej używanych algorytmów, których będziemy używać to: wyszukiwanie w pierwszej kolejności głębi (DFS) i wyszukiwanie w pierwszej kolejności szerokości (BFS).,
chociaż oba te algorytmy pozwalają nam na przemierzanie Wykresów, różnią się one w różny sposób. Zacznijmy od DFS.
DFS wykorzystuje w swojej implementacji filozofię „go deep, head first”. Chodzi o to, że zaczynając od początkowego wierzchołka (lub miejsca), idziemy jedną ścieżką aż do końca, a jeśli nie dotrzemy do celu, to wracamy i idziemy inną ścieżką.
spójrzmy na przykład., Załóżmy, że mamy skierowany wykres, który wygląda tak:

teraz chodzi o to, że zaczynamy od wierzchołka s i jesteśmy proszeni o znalezienie wierzchołka t. używając DFS, zamierzamy zbadać jedną ścieżkę, przejść całą drogę do końca, a jeśli nie znajdziemy t, to pójdziemy inną ścieżką., Oto proces:

w dół ścieżki pierwszego sąsiedniego wierzchołka
więc tutaj, idziemy ścieżką (P1) pierwszego sąsiedniego wierzchołka i widzimy, że nie jest to koniec, ponieważ ma ścieżkę do innego wierzchołka., Więc idziemy tą ścieżką:
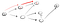
to wyraźnie nie jest wierzchołek t, więc musimy wrócić, ponieważ osiągnęliśmy ślepy zaułek. Ponieważ poprzedni węzeł nie ma już sąsiadów, wracamy do s., Z s przechodzimy do drugiego sąsiedniego węzła:
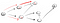
Idąc ścieżką (P2), mamy do czynienia z trzema sąsiadami., Ponieważ pierwsza z nich została już odwiedzona, musimy przejść w dół drugi:
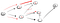
teraz po raz kolejny dotarliśmy do ślepego zaułka, który nie jest wierzchołkiem t, więc musimy wrócić., Ponieważ jest inny sąsiad, który nie został odwiedzony, idziemy w dół tej sąsiedniej ścieżki i w końcu znaleźliśmy wierzchołek t:

tak działa DFS. Idź ścieżką i idź dalej, dopóki nie dotrzesz do celu lub ślepego zaułka. Jeśli to cel, to koniec. Jeśli tak nie jest, wróć i kontynuuj inną ścieżkę, dopóki nie wyczerpasz wszystkich opcji w tej ścieżce.,
widzimy, że wykonujemy tę samą procedurę na każdym odwiedzanym wierzchołku:
wykonujemy DFS dla każdego sąsiada wierzchołka
ponieważ wymaga to wykonania tej samej procedury na każdym kroku, coś nam mówi, że będziemy musieli użyć rekurencji, aby zaimplementować ten algorytm.
oto kod w JavaScript:
Uwaga: Ten specyficzny algorytm DFS pozwala nam określić, czy jest możliwe dotarcie z jednego miejsca do kolejny., DFS może być używany na wiele sposobów i mogą wystąpić subtelne zmiany w powyższym algorytmie. Ogólna koncepcja pozostaje jednak taka sama.
Analiza DFS
teraz przeanalizujmy ten algorytm. Ponieważ przemierzamy każdy sąsiad węzła i ignorujemy odwiedzane, mamy runtime O (V + E).
szybkie wyjaśnienie, co dokładnie oznacza V+E:
V reprezentuje całkowitą liczbę wierzchołków. E oznacza całkowitą liczbę krawędzi. Każdy wierzchołek ma kilka krawędzi.,
choć może się wydawać, że można wierzyć, że jest to V•E zamiast V + E, zastanówmy się, co dokładnie oznacza V * e.aby coś było V * E, oznaczałoby to, że dla każdego wierzchołka musimy spojrzeć na wszystkie krawędzie grafu, niezależnie od tego, czy te krawędzie są połączone z danym wierzchołkiem.
podczas gdy, z drugiej strony, V + E oznacza, że dla każdego wierzchołka, patrzymy tylko na liczbę krawędzi, które odnoszą się do tego wierzchołka. Przypomnijmy z poprzedniego postu, że przestrzeń, którą zajmujemy dla listy adiacenckiej to O (V + E)., Każdy wierzchołek ma kilka krawędzi i w najgorszym przypadku, gdybyśmy mieli uruchomić DFS na każdym wierzchołku, wykonalibyśmy pracę O (V) wraz z badaniem wszystkich krawędzi wierzchołków, czyli O(E). Gdy spojrzymy na wszystkie liczby wierzchołków V, przyjrzymy się również sumie krawędzi E. Dlatego jest to V + E.
teraz, ponieważ DFS używa rekurencji na każdym wierzchołku, oznacza to, że używany jest stos (dlatego nazywa się to błędem przepełnienia stosu za każdym razem, gdy uruchamiasz nieskończone wywołanie rekurencyjne). Dlatego złożoność przestrzeni jest O (V).,
teraz zobaczmy, jak różni się wyszukiwanie w pierwszej kolejności.
Szerokość-pierwsze wyszukiwanie
Szerokość-pierwsze wyszukiwanie (BFS) podąża za filozofią „idź szeroko, z lotu ptaka”. Co to w zasadzie oznacza, że zamiast iść całą drogę w dół jednej ścieżki aż do końca, BFS porusza się w kierunku swojego miejsca przeznaczenia jeden sąsiad na raz., Spójrzmy co to oznacza:

więc zamiast po prostu przejść całą drogę w dół swojego pierwszego sąsiada, BFS najpierw odwiedzi wszystkich sąsiadów s, a następnie odwiedzi sąsiadów tych sąsiadów i tak dalej, aż osiągnie t.,fd17d”>


See how different DFS and BFS behave?, Chociaż lubię myśleć, że DFS lubi iść na czele, BFS lubi patrzeć powoli i obserwować wszystko krok po kroku.
teraz jedno pytanie, które nas wyróżnia, powinno brzmieć: „skąd wiemy, których sąsiadów odwiedzić najpierw od sąsiadów s?”
cóż, możemy użyć właściwości FIFO (first-in-first-out) kolejki, w której otwieramy pierwszy wierzchołek kolejki, dodajemy do niej jej nieodwiedzianych sąsiadów, a następnie kontynuujemy ten proces, aż kolejka będzie albo pusta, albo wierzchołek, który do niej dodajemy, będzie wierzchołkiem, którego szukaliśmy.,
teraz spójrzmy na kod w JavaScript:
Analiza BFS
może się wydawać, że BFS jest wolniejszy. Jeśli jednak uważnie przyjrzysz się wizualizacjom zarówno BFS, jak i DFS, zobaczysz, że w rzeczywistości mają one ten sam tryb runtime.
Kolejka zapewnia, że co najwyżej każdy wierzchołek będzie przetwarzany, dopóki nie dotrze do miejsca docelowego. Oznacza to, że w najgorszym przypadku BFS będzie również patrzeć na wszystkie wierzchołki i wszystkie krawędzie.,
podczas gdy BFS może wydawać się wolniejszy, jest faktycznie uważany za szybszy, ponieważ gdybyśmy mieli zaimplementować je na większych wykresach, przekonasz się, że DFS marnuje dużo czasu na przechodzenie długich ścieżek, które są ostatecznie błędne. W rzeczywistości BFS jest często używany w algorytmach do określania najkrótszej ścieżki z jednego wierzchołka do drugiego, ale zajmiemy się nimi później.
ponieważ czasy uruchamiania są takie same, BFS ma runtime O(V + E) i ze względu na użycie kolejki, która może pomieścić co najwyżej wierzchołki V, ma złożoność przestrzeni O (V).,
analogie do pomijania z
chcę zostawić cię z innymi sposobami, które osobiście wyobrażam sobie, jak działają DFS i BFS w nadziei, że pomoże Ci to zapamiętać.
ilekroć myślę o DFS, lubię myśleć o czymś, co znajduje właściwą ścieżkę, wpadając w wiele ślepych zaułków. Zazwyczaj to byłoby jak myszy przechodzące przez labirynt w poszukiwaniu jedzenia.,spróbuj ścieżki, dowiedz się, że ścieżka jest ślepym zaułkiem, a następnie przejdź do innej ścieżki i powtórz ten proces, aż osiągnie swój cel:

i tak wyglądałaby uproszczona wersja procesu:

teraz dla bfs, zawsze wyobrażałem sobie to jako tętnienie.,div>

podobnie jak BFS zaczyna się od źródła i odwiedza najpierw sąsiadów źródła, a następnie więcej na zewnątrz odwiedzając swoich sąsiadów i tak dalej:

podsumowanie
- głębokość-pierwsze wyszukiwanie (DFS) i szerokość-pierwsze wyszukiwanie (bfs) są używane do trawersowania Wykresów.,
- DFS ładuje jedną ścieżkę, dopóki nie wyczerpie tej ścieżki, aby znaleźć swój cel, podczas gdy BFS przemierza sąsiednie wierzchołki, aby znaleźć swój cel.
- DFS używa stosu, podczas gdy BFS używa kolejki.
- zarówno DFS, jak i BFS mają runtime O(V + E) i złożoność przestrzeni O(V).
- oba algorytmy mają różne filozofie, ale mają takie samo znaczenie w sposobie poruszania się grafami.