Rozkład prawdopodobieństwa / rodzaje rozkładów

wprowadzenie

Witamy w świecie prawdopodobieństwa w naukach o danych! Zacznę od intuicyjnego przykładu.

Załóżmy, że jesteś nauczycielem na Uniwersytecie. Po sprawdzeniu zadań przez tydzień, oceniłeś wszystkich uczniów. Dałeś te papiery kolesiowi z uniwersytetu i kazałeś mu stworzyć arkusz zawierający oceny wszystkich studentów., Ale facet przechowuje tylko oceny, a nie odpowiadających im uczniów.

popełnił kolejny błąd, w pośpiechu ominął kilka wpisów i nie mamy pojęcia, czyje oceny brakuje. Znajdźmy sposób, by to rozwiązać.

jednym ze sposobów jest wizualizacja ocen i sprawdzenie, czy można znaleźć trend w danych.

wykres, który masz Wykres nazywa się rozkładem częstotliwości danych. Widzisz, że istnieje gładka struktura podobna do krzywej, która definiuje nasze dane, ale czy zauważysz anomalię?, Mamy nienormalnie niską częstotliwość w określonym zakresie. Więc najlepiej byłoby mieć brakujące wartości, które usuwają wgniecenia w dystrybucji.

w ten sposób starasz się rozwiązać rzeczywisty problem za pomocą analizy danych. Dla każdego analityka danych, studenta lub praktykanta dystrybucja jest pojęciem obowiązkowym. Stanowi podstawę do analizy i wnioskowania statystyk.

podczas gdy pojęcie prawdopodobieństwa daje nam obliczenia matematyczne, rozkłady pomagają nam faktycznie wizualizować to, co dzieje się pod spodem.,

w tym artykule omówiłem kilka ważnych rozkładów prawdopodobieństwa, które są wyjaśnione w jasny i wyczerpujący sposób.

Uwaga: Ten artykuł zakłada, że masz podstawową wiedzę na temat prawdopodobieństwa. Jeśli nie, możesz odnieść się do tego rozkładu prawdopodobieństwa.,

spis treści

typowe typy danych
typy dystrybucji
1. rozkład Bernoulliego
2. rozkład jednolity
3. rozkład dwumianowy
4. rozkład normalny
5. rozkład Poissona
6. rozkład wykładniczy
relacje między dystrybucjami
Sprawdź swoją wiedzę!

typowe typy danych

zanim przejdziemy do wyjaśnienia dystrybucji, zobaczmy, jakie dane możemy napotkać. Dane mogą być dyskretne lub ciągłe.,

dane dyskretne, jak sama nazwa wskazuje, mogą przyjmować tylko określone wartości. Na przykład, gdy rzucisz matrycę, możliwe wyniki wynoszą 1, 2, 3, 4, 5 lub 6, a nie 1,5 lub 2,45.

dane ciągłe mogą przyjmować dowolną wartość w danym zakresie. Zakres może być skończony lub nieskończony. Na przykład, waga lub wzrost dziewczyny, długość drogi. Waga dziewczyny może być dowolną wartością od 54 kg lub 54,5 kg lub 54,5436 kg.

zacznijmy od typów dystrybucji.,

rodzaje dystrybucji

Dystrybucja Bernoulliego

Zacznijmy od najprostszej dystrybucji, jaką jest dystrybucja Bernoulliego. W rzeczywistości jest to łatwiejsze do zrozumienia niż się wydaje!

wy wszyscy ćpuny krykieta! Na początku każdego meczu krykieta, jak zdecydować, kto będzie bat lub piłka? Rzut! Wszystko zależy od tego, czy wygrasz czy przegrasz rzut, prawda? Powiedzmy, że jeśli rzucisz głową, wygrasz. Inaczej przegrasz. Nie ma midway.

rozkład Bernoulliego ma tylko dwa możliwe wyniki, a mianowicie 1 (sukces) i 0 (porażka) oraz jedną próbę., Tak więc zmienna losowa X, która ma rozkład Bernoulliego, może przyjąć wartość 1 z prawdopodobieństwem sukcesu, powiedzmy p, a wartość 0 z prawdopodobieństwem niepowodzenia, powiedzmy q lub 1-p.

tutaj wystąpienie głowy oznacza sukces, a wystąpienie ogona oznacza porażkę.
prawdopodobieństwo zdobycia głowy = 0,5 = prawdopodobieństwo zdobycia ogona, ponieważ są tylko dwa możliwe wyniki.

funkcja masy prawdopodobieństwa jest dana przez: px (1-p)1-x gdzie x € (0, 1).,
można go również zapisać jako

prawdopodobieństwo sukcesu i porażki nie musi być równie prawdopodobne, jak wynik walki między mną a Undertakerem. Jest prawie pewien, że wygra. Więc w tym przypadku prawdopodobieństwo mojego sukcesu wynosi 0.15, podczas gdy moja porażka wynosi 0.85

tutaj prawdopodobieństwo sukcesu(p) nie jest takie samo jak prawdopodobieństwo porażki. Poniższy wykres pokazuje rozkład Bernoulliego naszej walki.

tutaj prawdopodobieństwo sukcesu = 0.15 i prawdopodobieństwo porażki = 0.85., Wartość oczekiwana jest dokładnie tym, co brzmi. Jeśli cię uderzę, mogę oczekiwać, że mi oddasz. Zasadniczo wartość oczekiwana dowolnego rozkładu jest średnią rozkładu., Wartość oczekiwana zmiennej losowej X z rozkładu Bernoulliego znajduje się w następujący sposób:

E(X) = 1*P + 0*(1-p) = p

wariancja zmiennej losowej z rozkładu Bernoulliego wynosi:

V(X) = E(X2) – 2 = P – P2 = P(1-p)

istnieje wiele przykładów rozkładu Bernoulliego, takich jak to, czy jutro będzie padać, czy nie, gdzie deszcz oznacza sukces, a brak deszczu oznacza porażkę i wygraną (sukces) lub przegraną (porażkę) gry.

równomierny rozkład

kiedy rzucasz sprawiedliwą kostkę, wyniki są od 1 do 6., Prawdopodobieństwo uzyskania tych wyników jest równie prawdopodobne i jest to podstawa jednolitego rozkładu. W przeciwieństwie do rozkładu Bernoulliego, wszystkie n liczby możliwych wyników równomiernego rozkładu są jednakowo prawdopodobne.

zmienna X jest równomiernie rozłożona, jeśli funkcja gęstości jest:

wykres krzywej rozkładu jednorodnego wygląda następująco

można zobaczyć, że kształt krzywej rozkładu jednorodnego jest prostokątny, dlatego rozkład jednolity nazywa się rozkładem prostokątnym.,

dla równomiernego rozkładu, a i b są parametrami.

liczba bukietów sprzedawanych codziennie w kwiaciarni jest równomiernie rozłożona, maksymalnie 40 i minimum 10.

spróbujmy obliczyć prawdopodobieństwo, że dzienna sprzedaż spadnie między 15 a 30.

prawdopodobieństwo, że dzienna sprzedaż spadnie między 15 a 30 jest (30-15)*(1/(40-10)) = 0.5

podobnie prawdopodobieństwo, że dzienna sprzedaż jest większa niż 20, wynosi = 0.,667

średnia i wariancja X po równomiernym rozkładzie wynosi:

Średnia -> E(X) = (A+b)/2

wariancja -> V(X) = (b-a)2/12

standardowa gęstość jednorodna ma parametry a {\fncomic sans ms \ fs36} {\fncomic sans ms \ fs36} {\fncomic sans ms \ fs36} {\fncomic sans ms \ fs36} {\fncomic sans ms \ fs36} {\fncomic sans ms \ fs36} {\fncomic sans ms \ fs36} {\fncomic sans ms \ fs36} {\fncomic sans ms \ fs36 Załóżmy, że wygrałeś rzut dzisiaj i oznacza to udane wydarzenie. Znowu rzucasz, ale tym razem przegrałeś., Jeśli wygrasz rzut dzisiaj, nie wymaga to, że wygrasz rzut jutro. Przypiszmy zmienną losową, powiedzmy X, do liczby wygranych rzutów. Jaka może być możliwa wartość X? Może to być dowolna liczba w zależności od liczby razy rzuciłeś monetą.

są tylko dwa możliwe wyniki. Głowa oznacza sukces, a ogon-porażkę. Dlatego prawdopodobieństwo uzyskania głowy = 0,5 i prawdopodobieństwo niepowodzenia można łatwo obliczyć jako: q = 1-p = 0,5.,

rozkład, w którym możliwe są tylko dwa wyniki, takie jak sukces lub porażka, zysk lub strata, wygrana lub przegrana i gdzie prawdopodobieństwo sukcesu i porażki jest taka sama dla wszystkich prób nazywa się rozkład dwumianowy.

wyniki nie muszą być równie prawdopodobne. Pamiętasz przykład walki między mną a Undertakerem? Tak więc, jeśli prawdopodobieństwo sukcesu w eksperymencie wynosi 0,2 to prawdopodobieństwo niepowodzenia można łatwo obliczyć jako q = 1 – 0,2 = 0,8.

każda próba jest niezależna, ponieważ wynik poprzedniego rzutu nie determinuje ani nie wpływa na wynik bieżącego rzutu., Eksperyment z tylko dwoma możliwymi wynikami powtarzanymi n liczba razy nazywa się dwumianem. Parametry rozkładu dwumianowego są n I P, gdzie n jest całkowita liczba badań i p jest prawdopodobieństwo sukcesu w każdym badaniu.

na podstawie powyższego wyjaśnienia własności rozkładu dwumianowego są

każda próba jest niezależna.
w badaniu są tylko dwa możliwe wyniki-sukces lub porażka.
prawdopodobieństwo sukcesu i porażki jest takie samo dla wszystkich prób., (Próby są identyczne.,

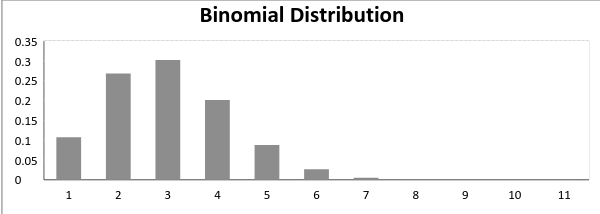
teraz, gdy prawdopodobieństwo sukcesu = prawdopodobieństwo porażki, w takiej sytuacji Wykres rozkładu dwumianowego wygląda następująco

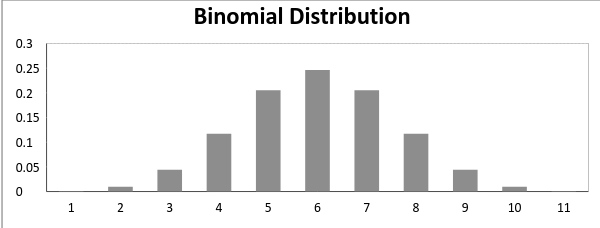
średnia i wariancja rozkładu dwumianowego są podane przez:

średnia -> µ = n*p

wariancja -> var(x) = n*p*q

rozkład normalny

rozkład normalny reprezentuje zachowanie większości sytuacji we wszechświecie (dlatego nazywa się go rozkładem „normalnym”., Chyba!). Duża suma (małych) zmiennych losowych często okazuje się być rozkładana normalnie, przyczyniając się do jej powszechnego zastosowania. Każdy rozkład jest znany jako rozkład normalny, jeśli ma następujące cechy:
1. średnia, mediana i tryb rozkładu pokrywają się.
2. krzywa rozkładu jest dzwonkowata i symetryczna względem linii x = μ.
3. całkowita powierzchnia pod krzywą wynosi 1.
4. dokładnie połowa wartości znajduje się po lewej stronie Centrum, a druga połowa po prawej.,
rozkład normalny jest bardzo różny od rozkładu dwumianowego. Jeśli jednak liczba prób zbliża się do nieskończoności, to kształty będą bardzo podobne.

PDF zmiennej losowej X po rozkładzie normalnym jest podany przez:

średnia i wariancja zmiennej losowej X, o której mówi się, że jest rozkładem normalnym, jest podana przez:

Średnia -> E(x) = µ

wariancja -> var(x) = σ^2

tutaj parametrami są µ (średnia) i σ (odchylenie standardowe).,
Wykres zmiennej losowej X ~ N (µ, σ) przedstawiono poniżej.

standardowy rozkład normalny jest zdefiniowany jako rozkład ze średnią 0 i odchyleniem standardowym 1. W takim przypadku plik PDF staje się:

Dystrybucja Poissona

Załóżmy, że pracujesz w call center, w przybliżeniu ile połączeń dostajesz dziennie? Może to być dowolna liczba. Cała liczba połączeń w call center w ciągu dnia jest wzorowana na dystrybucji Poissona., Więcej przykładów to
1. liczba połączeń alarmowych nagranych w szpitalu w ciągu dnia.
2. liczba kradzieży zgłoszonych na danym obszarze w ciągu dnia.
3. liczba klientów przybywających do salonu w ciągu godziny.
4. liczba samobójstw zgłoszonych w danym mieście.
5. liczba błędów drukarskich na każdej stronie książki.
Możesz teraz pomyśleć o wielu przykładach podążających za tym samym kursem., Rozkład Poissona ma zastosowanie w sytuacjach, w których zdarzenia zachodzą w losowych punktach czasu i przestrzeni, w których nasze zainteresowanie leży tylko w liczbie zdarzeń.

rozkład nazywa się rozkładem Poissona, gdy obowiązują następujące założenia:

1. Każde udane wydarzenie nie powinno mieć wpływu na wynik innego udanego wydarzenia.
2 . Prawdopodobieństwo sukcesu w krótkim przedziale musi być równe prawdopodobieństwu sukcesu w dłuższym przedziale.
3. Prawdopodobieństwo sukcesu w przedziale zbliża się do zera, gdy interwał staje się mniejszy.,

teraz, jeśli jakakolwiek dystrybucja potwierdza powyższe założenia, to jest dystrybucją Poissona. Niektóre notacje używane w rozkładzie Poissona to:
- λ to szybkość, z jaką występuje zdarzenie,
- t to długość przedziału czasu,
- I X to liczba zdarzeń w tym przedziale czasu.
tutaj X nazywa się zmienną losową Poissona, a rozkład prawdopodobieństwa X nazywa się rozkładem Poissona.

niech µ oznacza średnią liczbę zdarzeń w przedziale długości t. następnie µ = λ*t.,

wartość PMF X po rozkładzie Poissona jest podana przez:

średnia µ jest parametrem tego rozkładu. µ jest również definiowane jako długość λ razy tego przedziału. Wykres rozkładu Poissona przedstawiony jest poniżej:

Poniższy wykres ilustruje przesunięcie krzywej spowodowane wzrostem średniej.

zauważalne jest, że wraz ze wzrostem średniej krzywa przesuwa się w prawo.,

średnia i wariancja X po rozkładzie Poissona:

Średnia -> E(x) = µ
wariancja -> Var(X) = µ

rozkład wykładniczy

rozważmy jeszcze raz przykład call center. A co z odstępem czasu między połączeniami ? Tutaj na ratunek przychodzi nam rozkład wykładniczy. Rozkład wykładniczy modeluje odstęp czasu między wywołaniami.

inne przykłady to:

1. Długość czasu przyjazdu metra beteeen,
2., Długość czasu między przyjazdami na stację benzynową
3. Żywotność klimatyzatora

rozkład wykładniczy jest szeroko stosowany do analizy przeżywalności. Od oczekiwanej żywotności maszyny do oczekiwanej żywotności człowieka, rozkład wykładniczy z powodzeniem zapewnia wynik.

zmienna losowa X ma rozkład wykładniczy w formacie PDF:

f(x) = { λe-λx, x ≥ 0

i parametr λ>0, który jest również nazywany szybkością.,

dla analizy przeżycia, λ jest nazywany wskaźnikiem awaryjności urządzenia w dowolnym momencie t, biorąc pod uwagę, że przetrwało do t.

średnia i wariancja zmiennej losowej X po rozkładzie wykładniczym:

Średnia -> E(X) = 1/λ

wariancja -> var(x) = (1/λ)2

im większa szybkość, tym szybciej krzywa spada i im niższa szybkość, płaska krzywa. Jest to wyjaśnione lepiej na poniższym wykresie.,

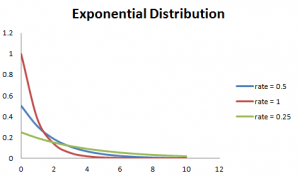
aby ułatwić obliczenia, poniżej podano kilka formuł.
P{x≤x} = 1 – e-λx, odpowiada obszarowi pod krzywą gęstości po lewej stronie x.

p{X>x} = e-λx, odpowiada obszarowi pod krzywą gęstości po prawej stronie x.

p{x1<X≤ x2} = e-λx1 – e-λx2, odpowiada powierzchni pod krzywą gęstości między X1 a X2.

relacje między dystrybucjami

relacje między dystrybucją Bernoulliego a dystrybucją Dwumianową

1., Dystrybucja Bernoulliego jest szczególnym przypadkiem dystrybucji Dwumianowej z pojedynczą próbą.

2. Istnieją tylko dwa możliwe wyniki rozkładu Bernoulliego i Dwumianu, mianowicie sukces i porażka.

3. Zarówno rozkład Bernoulliego, jak i rozkład dwumianowy mają niezależne szlaki.

zależność między rozkładem Poissona a rozkładem Dwumianowym

rozkład Poissona jest ograniczającym przypadkiem rozkładu dwumianowego w następujących warunkach:
1. liczba prób jest nieskończenie duża lub n → ∞.,
2. prawdopodobieństwo powodzenia każdej próby jest takie samo i nieskończenie małe lub p →0.
3. np = λ, jest skończona.
zależność między rozkładem normalnym i Dwumianowym& rozkład normalny i rozkład Poissona:

rozkład normalny jest inną ograniczającą formą rozkładu dwumianowego w następujących warunkach:
1. liczba prób jest nieskończenie duża, n → ∞.
2. zarówno p jak i q nie są nieskończenie małe.
rozkład normalny jest również ograniczającym przypadkiem rozkładu Poissona z parametrem λ →∞.,

relacja między rozkładem wykładniczym a rozkładem Poissona:

Jeśli czasy pomiędzy zdarzeniami losowymi następują po rozkładzie wykładniczym z szybkością λ, to całkowita liczba zdarzeń w przedziale czasowym długości t następuje po rozkładzie Poissona z parametrem λt.

Sprawdź swoją wiedzę

zaszedłeś tak daleko. Czy jesteś w stanie odpowiedzieć na następujące pytania? Dajcie znać w komentarzach poniżej!

1. Wzór do obliczenia standardowej normalnej zmiennej losowej wynosi:

A. (X+µ) / σ
b. (x-µ) / σ
c. (x-σ) / µ

2., W rozkładzie Bernoulliego wzór obliczania odchylenia standardowego jest podany przez:

a. P (1 – p)
b. sqrt(p(p – 1))
c. sqrt(p(1 – p))

3. Dla rozkładu normalnego, wzrost średniej będzie:

a. przesuń krzywą w lewo
b. przesuń krzywą w prawo
c. spłaszcz krzywą

4. Żywotność baterii rozkłada się wykładniczo z λ = 0,05 na godzinę. Prawdopodobieństwo, że bateria wytrzyma od 10 do 15 godzin wynosi:

a.0.1341
b.0.1540
c.0.,0079

Uwagi końcowe

rozkłady prawdopodobieństwa są powszechne w wielu sektorach, a mianowicie, ubezpieczenia, fizyka, inżynieria, Informatyka, a nawet Nauki społeczne, w którym studenci psychologii i medycyny są szeroko przy użyciu rozkładów prawdopodobieństwa. Ma łatwą aplikację i szerokie zastosowanie. W tym artykule podkreślono sześć ważnych rozkładów, które są obserwowane w codziennym życiu i wyjaśniono ich zastosowanie. Teraz będziesz w stanie zidentyfikować, powiązać i odróżnić między tymi dystrybucjami.,

Jeśli masz jakiekolwiek wątpliwości i chcesz zobaczyć więcej artykułów na temat dystrybucji, napisz w sekcji komentarzy poniżej. Aby uzyskać bardziej szczegółowy opis tych dystrybucji, możesz odnieść się do tego zasobu.