På denne siden, vil vi skissere tre prinsipper du bør forstå om serien kretser:
- Gjeldende: Den mengde strøm er den samme gjennom alle komponenter i en serie krets.
- Motstand: total motstand av noen serien krets er lik summen av de individuelle styrker.
- Spenning: nettspenning i en serie krets er lik summen av de enkelte spenningen synker.,
La oss ta en titt på noen eksempler på serien kretser som demonstrerer disse prinsippene.
Vi vil starte med en rekke krets som består av tre motstander og et enkelt batteri:

Det første prinsipp for å forstå om serien kretser er som følger:
mengden av gjeldende i en serie krets er den samme gjennom alle komponenter i kretsen.
Dette er fordi det er bare en vei for strømmen i en krets-serien., Fordi elektrisk ladning renner gjennom dirigenter som klinkekuler i en tube, vannføring (marmor hastighet) på noe punkt i kretsen (rør) på et bestemt punkt i tiden må være like.
ved Hjelp av Ohms Lov i Serien Kretser
Fra den måten at den 9-volts batteri er ordnet, kan vi fortelle at det er strøm i denne kretsen vil flyte i retning med klokken, fra punkt 1 til 2 til 3 til 4 og tilbake til 1. Vi har imidlertid en kilde til spenning og tre motstand. Hvordan kan vi bruke Ohms Lov her?,
En viktig påminnelse til Ohms Lov er at alle mengder (spenning, strøm, motstand og effekt) må forholde seg til hverandre i form av de samme to poeng i en krets. Vi kan se dette konseptet i aksjon i den ene motstanden krets eksempel nedenfor.,
ved Hjelp av Ohms Lov i en Enkel, Enkel Motstand Krets
Med en single-batteri, enkel motstand krets, kan vi enkelt beregne noen mengde fordi de alle er brukt til samme to poeng i kretsen:


Siden punktene 1 og 2 er koblet sammen med wire av ubetydelig motstand, som er punktene 3 og 4, kan vi si at punkt 1 er elektrisk felles punkt 2 og punkt 3 er elektrisk felles til punkt 4., Siden vi vet at vi har 9 volt electromotive kraft mellom punktene 1 og 4 (rett over på batteriet), og siden punkt 2 er felles for punkt 1 og punkt 3 er felles for punkt 4, må vi også ha 9 volt mellom punkt 2 og 3 (direkte over motstanden).
Derfor, vi kan anvende Ohms Lov (I = E/R) til strøm gjennom resistoren, fordi vi vet at spenningen (E) over motstand og motstand (R) for at motstand. Alle vilkårene (E, I, R) gjelder det samme to poeng i kretsen, til den samme motstand, så vi kan bruke Ohms Lov formula uten reservasjon.,
ved Hjelp av Ohms Lov i Kretser med Flere Motstander
I kretser som inneholder mer enn én motstand, må vi være forsiktig med hvordan vi bruker Ohms Lov. I tre-motstand eksempel krets nedenfor, vet vi at vi har 9 volt mellom punktene 1 og 4, som er beløpet for electromotive force kjører strøm gjennom serien kombinasjon av R1, R2 og R3. Vi kan imidlertid ikke ta verdien av 9 volt, og dele det med 3k, eller 5k 10k Ω for å prøve å finne en aktuell verdi, fordi vi ikke vet hvor mye spenning er over noen av disse motstander, individuelt.,

figur 9 volt er en total mengde for hele kretsen, mens tallene for 3k, 10k, og 5k Ω er individuelle mengder for individuelle motstander. Hvis vi skulle sett en figur for full spenning i en Ohms Lov ligning med et tall for individuell motstand, ville resultatet ikke forholder seg nøyaktig til enhver mengde i den virkelige krets.,
For R1, Ohms Lov vil forholde seg mengden av spenning over R1 med gjeldende gjennom R1, gitt R1 ‘ s resistance, 3kΩ:

Men, siden vi ikke vet hvilken spenning over R1 (bare den totale spenningen er levert av batteriet over tre-motstand serie kombinasjon) og vi vet ikke gjeldende gjennom R1, vi kan ikke gjøre noen beregninger med enten formel. Det samme gjelder for R2 og R3: vi kan anvende Ohms Lov formler hvis og bare hvis alle vilkårene er representative for sine respektive mengder mellom de samme to poeng i kretsen.,
Så hva kan vi gjøre? Vi kjenner spenning på kilden (9 volt) anvendes på tvers av serien kombinasjon av R1, R2 og R3, og vi vet at motstanden i hver motstand, men siden disse mengdene er ikke i samme kontekst, kan vi ikke bruke Ohms Lov til å bestemme krets gjeldende. Hvis bare vi visste hva den totale motstanden var for kretsen: da kan vi beregne den totale strømmen med våre tall for total spenning (i=E/R).,
Kombinere Flere Motstander i en Tilsvarende Sum Motstand
Dette bringer oss til det andre prinsippet i serien kretser:
Den totale motstanden i eventuelle serien krets er lik summen av de individuelle styrker.
Dette bør gjøre intuitiv følelse: jo mer motstander i serien er at den nåværende må strømme gjennom, jo vanskeligere vil det være for den aktuelle til å flyte.,
I eksempelet problem, vi hadde en 3 kΩ, 10 kΩ, og 5 kΩ motstander i serien, noe som gir oss en total motstand av 18 kΩ:

I hovedsak, vi har beregnet tilsvarende motstand av R1, R2 og R3 kombinert.,oltages ved Hjelp av Ohms Lov
å Vite at strømmen er lik gjennom alle komponenter i en serie krets (og vi har bare bestemt den gjeldende gjennom batteriet), kan vi gå tilbake til vår opprinnelige kretsen skjematisk og merk gjeldende gjennom hver komponent:
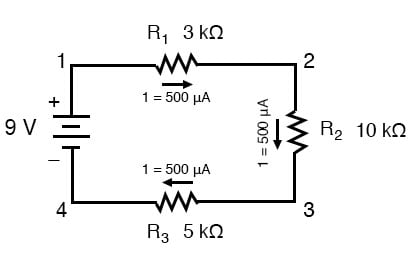
Nå som vi vet hvor mye strøm gjennom hver motstand, vi kan bruke Ohms Lov til å bestemme spenningsfallet over hver og en (gjelder Ohms Lov i sin rette sammenheng):

legg Merke til at spenningen faller over hver motstand, og hvordan summen av spenningen faller (1.,5 + 5 + 2.5) er lik batteriet (forsyning) spenning: 9 volt.
Dette er det tredje prinsippet om serien kretser:
spenning i en serie krets er lik summen av de enkelte spenningen synker.
Analyse av Enkle Serie-Kretser med «Tabell Metoden» og Ohms Lov
Men den metoden vi bare brukt til å analysere denne enkle serie-krets kan være strømlinjeformet for bedre forståelse., Ved hjelp av en tabell for å vise alle spenning, strøm og motstand i kretsen, det blir veldig lett å se hvilke av disse kvanta kan være riktig relatert til Ohms Lov ligningen:

regelen med en slik tabell er å bruke Ohms Lov til verdier innenfor hvert vertikal kolonne. For eksempel, ER1 bare med IR1 og R1; ER2 bare med IR2 og R2, etc., Du begynner analysen med å fylle inn de elementene i tabellen som er gitt til deg fra begynnelsen:

Som du kan se fra den ordning av data, kan vi ikke anvende 9 volt OG (total spenning) til noen av motstand (R1, R2 eller R3) i noen Ohms Lov formelen fordi de er i forskjellige kolonner. 9 volt batteri spenning er ikke påføres direkte på tvers av R1, R2 eller R3. Men, vi kan bruke vår «regler» av serien kretser for å fylle ut blanke flekker på en horisontal rad.,t 500 μa:

Så, vel vitende om at den nåværende er delt likt av alle komponenter i en serie krets (en annen «regelen» av serien kretser), vi kan fylle i de strømmer til hver motstand fra dagens tall bare beregnet:

til Slutt, kan vi bruke Ohms Lov til å bestemme spenningsfallet over hver motstand, en kolonne på en gang:

Verifisere Beregninger med Datamaskinen Analyse (SPICE)
Bare for moro skyld, vi kan bruke en datamaskin til å analysere denne samme krets automatisk., Det vil være en god måte å kontrollere våre beregninger, og også bli mer kjent med datamaskinen analyse. For det første har vi for å beskrive den kretsen til datamaskinen i et format som gjenkjennes av programvaren.
KRYDDER programmet vi skal bruke, krever at all elektrisk unike poeng i en krets være nummerert, og komponent plassering er forstått av hvilke av de nummererte punktene, eller «noder» de deler. For å klargjøre, jeg mønstret av de fire hjørnene i vårt eksempel krets 1 til 4., SPICE, men krever at det er en node null et sted i kretsen, så jeg skal tegne krets, endre nummereringen litt:

Alt jeg har gjort her er re-nummererte nedre venstre hjørne av kretsen 0 i stedet for 4. Nå, jeg kan legge inn flere linjer med tekst i en datamaskin fil som beskriver krets i form SPICE vil forstå, komplett med et par ekstra linjer med kode for å styre programmet for å vise spenning og strøm data for vår fornøyelse., Denne datamaskinen filen er kjent som netlist i SPICE-terminologi:
series circuit v1 1 0 r1 1 2 3k r2 2 3 10k r3 3 0 5k .dc v1 9 9 1 .print dc v(1,2) v(2,3) v(3,0) .end
Nå, alt jeg trenger å gjøre er å kjøre KRYDDER program for å behandle netlist og output resultater:
| v1 | v(1,2) | v(2,3) | – v(3) | jeg(v1) |
|---|---|---|---|---|
| 9.000 E+00 | 1.500 E+00 | 5.000 E+00 | 2.500 E+00 | -5.,000E-04 |
Dette utskriften er å fortelle oss batterispenningen er 9 volt, og spenningen faller på tvers av R1, R2 og R3 er 1,5 volt, 5 volt, og 2,5 volt, henholdsvis. Spenningen faller på tvers av enhver komponent som er i SPICE er referert til noden tall komponenten ligger mellom, slik at v(1,2) refererer til spenningen mellom noder 1 og 2 i kretsen, som er de punktene som mellom R1 er plassert.,
rekkefølgen på node nummer er viktig: når SPICE utganger en figur for v(1,2), det gjelder polariteten på samme måte som om vi var å holde et voltmeter med rødt test føre på node 1 og svart test føre på node 2. Vi har også et display som viser gjeldende (riktignok med en negativ verdi) på 0,5 milliampere eller 500 mikroampere. Så vår matematisk analyse har blitt stadfestet av datamaskinen. Denne figuren vises som et negativt tall i SPICE analyse, på grunn av en egenskap i veien SPICE håndterer dagens beregninger.,
I sammendraget, en serie krets er definert som det å ha bare én vei gjennom som strømmen kan flyte. Fra denne definisjonen, tre reglene for serien kretser følger: alle komponenter dele samme gjeldende; motstand legge til lik en større, total motstand, og spenningen synker legge til lik en større, total spenning. Alle disse reglene finne roten i definisjonen av en serie krets. Hvis du forstår at definisjonen fullt, da reglene er noe mer enn fotnoter til en definisjon.
ANMELDELSE:
- Komponentene i en serie krets dele samme gjeldende: ITotal = I1 = I2 = . . ., I
- Den totale motstanden i en serie krets er lik summen av de individuelle styrker: RTotal = R1 + R2 + . . . Rn
- Totale spenningen i en serie krets er lik summen av de enkelte spenningen faller ETotal = E1 + E2 + . . . No
Prøv ut våre Ohms Lov Kalkulator i våre Verktøy-seksjonen.
i SLEKT REGNEARK:
- Serie DC Kretser Praksis Regneark med Svar Regneark
- Algebraisk Ligning Manipulasjon for Elektriske Kretser Regneark