En ting som vi skal gjøre mye med algoritmer i denne serien er grafen traversal. Hva betyr dette egentlig?
i Utgangspunktet, ideen er at vi skal flytte seg rundt på grafen fra en toppunktet til en annen, og å oppdage egenskapene deres sammenhengende forhold.
To av de mest brukte algoritmene som vi kommer til å bruke mye, er: Dybde-Først Søk (DFS) og Bredde-Først Søk (BFS).,
Mens begge disse algoritmene tillate oss å traversering av grafer, de skiller seg i varierende måter. La oss starte med DFS.
DFS bruker «gå dypt, med hodet først» filosofi i sin gjennomføring. Ideen er at du starter fra en første toppunktet (eller sted), kan vi gå ned en sti til vi kommer slutten, og hvis vi ikke nå vårt mål, så kommer vi tilbake og gå ned en annen vei.
La oss se på et eksempel., Anta at vi har en rettet graf som ser ut som dette:

Nå ideen er at vi starter på vertex-s, og vi er bedt om å finne toppunkt t. Ved hjelp av DFS, vi kommer til å utforske en bane, gå helt til enden, og hvis vi ikke finner t, så går vi ned en annen vei., Her er prosessen:

Så her går vi ned den veien (p1) i det første nærliggende toppunkt og vi ser at det er ikke slutt fordi det har en vei mot en annen toppunktet., Så går vi ned denne banen:
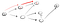
Dette er helt klart ikke toppunktet t så vi må gå tilbake fordi vi nådd en dead end. Siden den forrige noden har ikke lenger naboer, går vi tilbake til s., Fra s, vi går til sin andre nærliggende node:
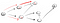
du Går nedover stien (p2), vi blir konfrontert med tre naboer., Siden den første har allerede blitt besøkt, har vi å gå ned den andre:
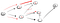
Nå, igjen har vi nådd en blindvei som ikke er toppunktet t så vi må gå tilbake., Siden det er en annen nabo som ikke har vært besøkt, vi går ned på den nærliggende banen og til sist fant vi toppunktet t:

Dette er hvordan DFS fungerer. Gå ned en sti og holde det gående til du har nådd målet eller en dead end. Hvis det er målet, så er du ferdig. Hvis det ikke, så kan du gå tilbake og fortsett ned en annen vei til du har brukt opp alle alternativer innen denne banen.,
Vi kan se at vi følger samme prosedyre som ved hvert knutepunkt at vi besøk:
Gjør et DFS for hver nabo til toppunktet
Siden dette innebærer å gjøre den samme prosedyren på hvert trinn, noe som forteller oss at vi trenger å bruke recursion å implementere denne algoritmen.
Her er kode i JavaScript:
Merk: Denne spesifikke DFS algoritme gjør det mulig for oss å fastslå om det er mulig å komme seg fra ett sted til et annet., DFS kan brukes i en rekke måter, og det kan være subtile endringer i algoritmen ovenfor. Men det generelle konseptet er fortsatt det samme.
Analyse av DFS
la oss Nå analysere denne algoritmen. Siden vi krysser gjennom hver nabo av noden og vi ignorerer besøkte seg, vi har en kjøretid på O(V + E).
En rask forklaring på akkurat hva V+E betyr følgende:
V er det totale antall noder. E representerer det totale antallet kanter. Hver toppunktet har en rekke kanter.,
Mens det kan virke som man kan bli ledet til å tro at det er V•E i stedet for V + E, la oss tenke på hva V•E betyr nøyaktig.For at noe skal være V•E, ville det bety at for hvert knutepunkt, må vi se på alle kantene i grafen uavhengig av om eller ikke de kanter er koblet til en bestemt toppunktet.
Mens du, på den annen side, V + E betyr at for hver toppunktet, vi bare ser på antall kanter som gjelder for at et toppunkt. Husker fra forrige innlegg, at det rommet vi ta opp for adjacency listen er O(V + E)., Hver toppunktet har en rekke kanter og i verste fall, hvis vi skulle kjør DFS på hver toppunktet, vi ville ha gjort O(V) arbeidet sammen med utforske alle kanter av knutepunktene, som er O(E). Når vi har sett på alle V antall noder, ville vi også ha sett på en sum av E kantene. Derfor er det V + E.
Nå, siden DFS bruker recursion på hver toppunktet, som betyr at en stakk er brukt (som er grunnen til at det kalles en stack overflow error når du kjører inn i en uendelig rekursiv samtale). Derfor plass kompleksiteten er O(V).,
la oss Nå se hvordan bredde-først søk er forskjellig.
Bredde-Først Søk
Bredde-Først Søk (BFS) følger «gå bredt, bird ‘ s eye-view» – filosofi. Hva som i utgangspunktet betyr er at i stedet for å gå hele veien ned en sti til slutten, BFS beveger seg mot målet naboen med en gang., La oss se på hva det betyr:

Så i stedet for bare å gå hele veien ned sin første nabo, BFS ville besøke alle naboer av s første og deretter går de til naboene naboer og så videre helt til den når t.,fd17d»> 

See how different DFS and BFS behave?, Mens jeg liker å tenke at DFS liker å gå på hodet, BFS liker å lete ta det sakte og observere alt ett skritt av gangen.
Nå ett spørsmål som skiller seg ut for oss, skal være: «Hvordan vet vi som naboer å besøke først fra s’ s naboer?»
Vel, vi kunne bruke en kø er først-inn-først-ut (FIFO) eiendom der vi pop første toppunktet av køen, legg den ubenyttede naboer til køen, og trykk deretter på fortsett denne prosessen til køen er enten tom eller toppunktet vi legge til det er toppunktet vi har vært på jakt etter.,
la oss Nå se på koden i JavaScript:
Analyse av BFS
Det kan virke som BFS er tregere. Men hvis du ser nøye på effekter av både BFS og DFS, vil du finne at de faktisk har samme kjøring.
køen sikrer at på de fleste hver toppunktet vil bli behandlet før det kommer frem til destinasjonen. Så det betyr i verste fall, BFS vil også se på alle hjørner og alle kanter.,
Mens BFS kan virke tregere, det er faktisk anses raskere fordi hvis vi skulle implementere dem i større grafer, vil du finne at DFS avfall mye tid på å gå ned lange baner som til syvende og sist er galt. Faktisk, BFS er ofte brukt i algoritmer for å finne korteste vei fra en toppunktet til en annen, men vi vil komme inn på disse senere.
Så siden runtimes er den samme, BFS har en kjøretid på O(V + E) og på grunn av bruk av en kø som kan holde på mest V hjørnene, det har en plass kompleksitet O(V).,
Analogier til å Forlate Av Med
jeg vil forlate deg med andre måter som jeg personlig forestille seg hvordan DFS og BFS arbeid i håp om at det vil hjelpe deg å huske så godt.
Når jeg tenker på DFS, jeg liker å tenke på noe som finner rett vei ved å komme borti mange blindveier. Vanligvis, ville dette være som en mus går gjennom en labyrint for å lete etter mat.,ville du prøve en vei, og finner ut at veien er en blindvei, så pivot til en annen bane og gjenta denne prosessen til den når sitt mål:

Og dette er hva som er en forenklet versjon av prosessen vil se ut:

Nå for BFS, Jeg har alltid forestilt meg det som en krusning.,div>

Mye som hvordan BFS starter ved kilden og besøk på kilden naboer først, og deretter går mer utover ved å besøke deres naboer og så videre:

Oppsummering
- Dybde-Først Søk (DFS) og Bredde-Først Søk (BFS) er begge brukt til å gå gjennom grafer.,
- DFS kostnader ned en sti til den er utslitt at veien til å finne sitt mål, mens BFS bølger som sprer seg gjennom nærliggende noder for å finne sitt mål.
- DFS bruker en stabel mens BFS bruker en kø.
- Både DFS og BFS har en kjøretid på O(V + E) og en plass kompleksitet O(V).
- Begge algoritmene har ulike filosofier, men deler like viktig i hvordan vi traversering av grafer.