Madame Lelica

Innledning

Velkommen til en verden av Sannsynlighet i Data Vitenskap! La meg starte ting av med et enkelt eksempel.

Tenk deg at du er en lærer ved et universitet. Etter å ha sjekket oppdrag for en uke, har du gradert alle studentene. Du ga disse gradert papir til data-entry fyr i universitets-og fortelle ham til å opprette et regneark som inneholder karakterer av alle studentene., Men fyren bare lagrer karakterer, og ikke tilsvarende for studenter.

Han gjorde en blunder, han tapte et par av oppføringer i en hast, og vi har ingen anelse om karakterer som mangler. La oss finne en måte å løse dette.

En måte er at du visualisere karakterer og se om du kan finne en trend i dataene.

grafen at du har plottet er kalt frekvens distribusjon av data. Du ser at det er en jevn kurve som struktur som definerer våre data, men gjør du oppdager et avvik?, Vi har en unormalt lav frekvens på en bestemt poengsum utvalg. Så den beste gjetning vil være å ha manglende verdier som fjerner forskjell i fordelingen.

Dette er hvordan du ville prøve å løse virkelige problemer med å bruke data-analyse. For Data som Forsker, student eller praktikant, distribusjon er en må kjenne til konseptet. Det gir grunnlag for analyse og slutningsstatistikk.

Mens begrepet sannsynlighet gir oss den matematiske beregninger, distribusjoner hjelpe oss faktisk visualisere hva som skjer under.,

I denne artikkelen, jeg har dekket noen viktige sannsynlighetsfordelinger som er forklart i en klar, så vel som omfattende måte.

Merk: Denne artikkelen forutsetter at du har en grunnleggende kunnskap om sannsynlighet. Hvis ikke, kan du se denne sannsynlighetsfordelinger.,

Innholdsfortegnelse

– >

1. Vanlige Datatyper
2. Typer Utdelinger
   1. Bernoulli Distribusjon
   2. Jevn Fordeling
   3. Binominal Distribusjon
   4. Normal Distribusjon
   5. Poisson-Distribusjonen
   6. Eksponensiell Fordeling
3. Forholdet mellom Distribusjoner
4. Test dine Kunnskaper!

Vanlige Datatyper

Før vi hopper på forklaring av fordelinger, la oss se hva slags data kan vi støte på. Dataene kan være diskret eller kontinuerlig.,

Diskrete Data, som navnet antyder, kan bare ta angitte verdier. For eksempel, når du kaster en terning, de mulige utfallene er 1, 2, 3, 4, 5 eller 6, og ikke 1,5 eller 2.45.

Kontinuerlig Data kan ta noen verdi innen et gitt område. Rekkevidden kan være endelig eller uendelig. For eksempel, En jente i vekt eller høyde, lengde av veien. Vekten av en jente kan være hvilken som helst verdi fra 54 kg, eller på 54,5 kg, eller 54.5436 kg.

Nå la oss starte med typer distribusjoner.,

Typer Utdelinger

Bernoulli Distribusjon

La oss starte med det enkleste distribusjon som er Bernoulli Distribusjon. Det er faktisk enklere å forstå enn det høres ut!

Alt du cricket junkies ut det! I begynnelsen av alle cricket kamp, hvordan gjør du som bestemmer hvem som kommer til å slå eller ball? En kaste! Det hele avhenger av om du vinner eller taper, kaste, ikke sant? La oss si at hvis kaste resultater i et hode, du vinner. Andre, taper du. Det er ingen midtveis.

En Bernoulli-distribusjonen har bare to mulige utfall, nemlig 1 (suksess) og 0 (failure), og en enkelt studie., Så tilfeldig variabel X som har en Bernoulli-distribusjon kan ta verdien 1 med sannsynlighet for suksess, si, p, og verdien 0 med sannsynlighet for svikt, sier q-eller 1-p.

Her forekomsten av et hode betegner suksess, og forekomsten av en hale indikerer feil.
Sannsynligheten for å få et hode = 0.5 = Sannsynligheten for å få en hale siden det bare er to mulige utfall.

sannsynligheten masse funksjon er gitt ved: px(1-p)1-x der x € (0, 1).,
Det kan også skrives som

sannsynlighetene for suksess og fiasko trenger ikke være like sannsynlig som et resultat av en kamp mellom meg og Undertaker. Han er ganske mye sikker på å vinne. Så i dette tilfellet er sannsynligheten for min suksess er 0.15, mens mine feil er 0.85

Her er det stor sannsynlighet for suksess(p) er ikke samme som sannsynligheten for å mislykkes. Slik diagrammet under viser Bernoulli Distribusjon av våre kampen.

Her er det stor sannsynlighet for suksess = 0.15 og sannsynligheten for svikt = 0.85., Forventet verdi er akkurat hva det høres ut. Hvis jeg slå deg, jeg kan forvente deg til å sparke meg tilbake. I utgangspunktet forventet verdi av alle distribusjon er gjennomsnittet av fordelingen., Den forventede verdien av en tilfeldig variabel X fra en Bernoulli-distribusjon er funnet som følger:

E(X) = 1*p + 0*(1-p) = p

variansen av en tilfeldig variabel fra en bernoulli-distribusjon er:

V(X) = E(X2) – 2 = p – p2 = p(1-p)

Det er mange eksempler på Bernoulli distribusjon, for eksempel om det er regn i morgen eller ikke der regn betegner suksess og ingen regn indikerer svikt og Vinne (suksess) eller å miste (failure) spillet.

Jevn Fordeling

Når du ruller en virkelig dø, resultatene 1 til 6., Sannsynligheten for å få disse utfallene er like sannsynlige, og som er grunnlaget for en jevn fordeling. I motsetning til Bernoulli Distribusjon, alle n antall mulige utfall av en uniform fordeling er like sannsynlige.

En variabel X sies å være jevnt fordelt hvis tetthetsfunksjonen er:

grafen til en jevn fordeling kurven ser ut som

Du kan se at formen på Uniform fordeling kurve er rektangulær, grunnen til at Jevn fordeling kalles rektangulær fordeling.,

For en Jevn Fordeling, a og b er parametre.

antall buketter som selges daglig på en blomsterbutikk er jevnt fordelt, med et maksimum på 40 og en minimum av 10.

La oss prøve å beregne sannsynligheten for at den daglige salget vil falle mellom 15 og 30.

sannsynligheten for at daglige salget vil falle mellom 15 og 30 er (30-15)*(1/(40-10)) = 0.5

på samme måte er det stor sannsynlighet at daglige salget er større enn 20 er = 0.,667

forventningen og variansen til X etter en jevn fordeling er:

Mener -> E(X) = (a+b)/2

Varians -> V(X) = (b-a)2/12

standard uniform tetthet har parametre a = 0 og b = 1, slik at PDF-filen for standard uniform tetthet er gitt ved:

Binominal Distribusjon

La oss komme tilbake til cricket. Anta at du vil kaste i dag, og dette indikerer et vellykket arrangement. Du legger igjen, men du har tapt denne gangen., Hvis du vinner en kaste i dag, er dette ikke nødvendiggjør at du vil vinne og kron i morgen. La oss tilordne en tilfeldig variabel, si X antall ganger du vil kaste. Hva som kan være mulig verdi av X? Det kan være en rekke avhengig av antall ganger du kastet en mynt.

Det er bare to mulige utfall. Hode betegner suksess og hale betegner feil. Derfor er sannsynligheten for å få et hode = 0.5 og sannsynligheten for svikt kan være lett beregnet som: q = 1 – p = 0.5.,

En fordeling der bare to utfall er mulig, for eksempel suksess eller fiasko, gevinst eller tap, vinner eller taper, og der sannsynligheten for suksess og fiasko er den samme for alle prøvelsene er kalt en Binominal Distribusjon.

resultatene trenger ikke være like sannsynlig. Husk eksempel på en kamp mellom meg og Undertaker? Så, hvis sannsynligheten for suksess i et eksperiment er 0,2 så sannsynligheten for svikt kan være lett beregnet som q = 1 – 0.2 = 0.8.

Hver studie er uavhengige siden resultatet av den forrige kast ikke bestemme eller påvirke utfallet av gjeldende kaste., Et eksperiment med bare to mulige utfall gjentatt n antall ganger kalles binomiske. Parameterne for en binominal distribusjon er n og s, der n er det totale antall forsøk, og p er sannsynligheten for suksess i hvert forsøk.

På grunnlag av de ovennevnte forklaring, egenskapene til en Binominal Distribusjon er

1. Hvert forsøk er uavhengige.
2. Det er bare to mulige utfall i en prøve – enten en suksess eller en fiasko.
3. Et totalt antall på n identiske studier er gjennomført.
4. sannsynligheten for suksess og fiasko er den samme for alle prøvelser., (Studier er identiske.,

   

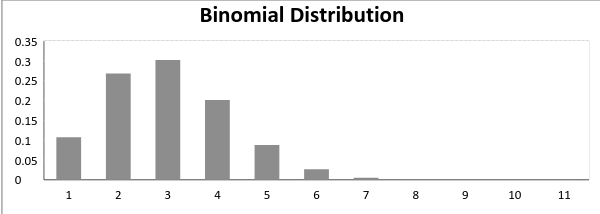
   Nå, når sannsynligheten for suksess = sannsynligheten for feil i en slik situasjon grafen til binomiske fordelingen ser ut som

   

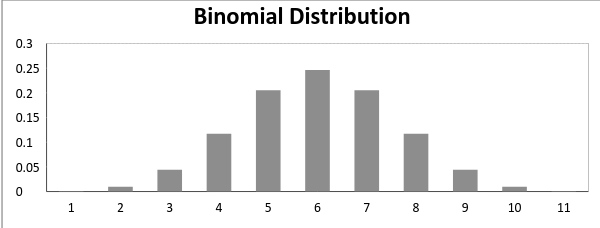
   forventningen og variansen av en binomial fordeling er gitt ved:

   Mener -> µ = n*p

   Varians -> Var(X) = n*p*q

   Normal Distribusjon

   Normal fordeling representerer oppførselen til de fleste situasjoner i universet (Det er derfor det kalles en «normal» fordeling., Jeg antar!). Den store summen av (små) tilfeldige variabler viser seg ofte å være normalfordelt, kan bidra til bred anvendelse. Alle distribusjon er kjent som Normal distribusjon hvis den har følgende egenskaper:

   1. mean, median og modus for distribusjon sammenfallende.
   2. kurven av fordelingen er bell-formet og symmetrisk om linjen x=μ.
   3. Det totale arealet under kurven er 1.
   4. Nøyaktig halvparten av verdiene som er til venstre for midten og den andre halvparten til høyre.,

   En normal fordeling er svært forskjellige fra Binominal Distribusjon. Imidlertid, hvis antall forsøk tilnærminger infinity deretter former vil være ganske lik.

   PDF av en tilfeldig variabel X etter en normal fordeling er gitt ved:

   

   forventningen og variansen av en tilfeldig variabel X som sies å være normalfordelt er gitt ved:

   Mener -> E(X) = µ

   Varians -> Var(X) = σ^2

   Her er µ (mean) og σ (standardavvik) er parameterne.,
   grafen til en tilfeldig variabel X ~ N (µ, σ) er vist nedenfor.

   

   En standard normalfordeling er definert som distribusjon med middelverdi 0 og standardavvik 1. For et slikt tilfelle, PDF-filen blir:

   

   

   Poisson-Distribusjonen

   Tenk deg at du jobber på et call center, omtrent hvor mange samtaler får du på en dag? Det kan være hvilket som helst tall. Nå, hele antall samtaler på et call center i dag er modellert ved Poisson-fordelingen., Noen flere eksempler er

   1. antall nødanrop er tatt opp på et sykehus i løpet av en dag.
   2. antall tyverier rapportert i et område på en dag.
   3. antall kunder som kommer på en salong i en time.
   4. antall selvmord rapportert i en bestemt by.
   5. antall trykkfeil på hver side av boken.

   Du kan nå tror mange eksempler å følge samme kurs., Poisson-Fordelingen er aktuelt i situasjoner hvor det oppstår hendelser på vilkårlige punkter i tid og rom, hvor vår interesse ligger bare i antall forekomster av den hendelsen.

   En fordeling kalles Poisson-fordeling når følgende forutsetninger gjelder:

   1. Et vellykket arrangement skal ikke påvirke utfallet av en annen vellykket arrangement.
   2. Sannsynligheten for suksess over et kort intervall må være lik sannsynligheten for suksess over et lengre intervall.
   3. Sannsynligheten for suksess i et intervall nærmer seg null, så intervallet blir mindre.,

   Nå, hvis noen distribusjon validerer de ovennevnte forutsetninger så er det en Poisson-fordeling. Noen merknader som brukes i Poisson-fordelingen er:

   • λ er den hastigheten som en hendelse inntreffer,
   • t er lengden av et tidsintervall,
   • Og X er antall hendelser i at tidsintervall.

   Her, X kalles en Poisson Tilfeldig Variabel og sannsynligheten for distribusjon av X kalles Poisson-fordelingen.

   La µ angir gjennomsnittlig antall hendelser i et intervall av lengde t. Så, µ = λ*t.,

   PMF av X etter en Poisson-fordelingen er gitt ved:

   

   Det betyr µ er den parameteren for denne fordelingen. æ er også definert som λ ganger lengden av intervallet. Grafen til en Poisson-fordelingen er vist nedenfor:

   

   grafen som er vist nedenfor illustrerer skift i kurven på grunn av økning i mener.

   

   Det er merkbar at som betyr øker, kurven skifter til høyre.,

   forventningen og variansen til X etter en Poisson-fordeling:

   Mener -> E(X) = µ
   Varians -> Var(X) = µ

   Eksponensiell Fordeling

   La oss vurdere call center eksempel en gang. Hva om tidsintervallet mellom samtalene ? Her eksponentielle fordelingen kommer til vår unnsetning. Eksponentiell fordeling modeller tidsintervallet mellom samtalene.

   Andre eksempler er:

   1. Lengden av tid beteeen t ankomster,
   2., Tiden mellom ankomster på en bensinstasjon
   3. Livet til en Air Conditioner

   Eksponentielle fordelingen er mye brukt for å overleve analyse. Fra forventet levetid for en maskin til forventet levetid for et menneske, eksponentiell fordeling vellykket leverer resultatet.

   En tilfeldig variabel X er sagt å ha en eksponentiell fordeling med PDF-fil:

   f(x) = { λe-λx, x ≥ 0

   og parameteren λ>0, som også kalles pris.,

   For å overleve analyse, λ kalles svikt pris for en enhet og ikke på noe tidspunkt t, gitt at den har overlevd opp til t.

   forventningen og Variansen av en tilfeldig variabel X etter en eksponentiell fordeling:

   Mener -> E(X) = 1/λ

   Varians -> Var(X) = (1/λ)2

   Også, jo høyere pris, jo raskere kurven faller og lavere pris, flatere kurven. Dette er forklart bedre med grafen som er vist nedenfor.,

   

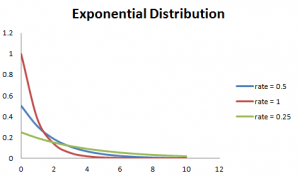
   for Å lette utregningen, det er noen formler som er gitt nedenfor.
   P{X≤x} = 1 – e-λx, tilsvarer det området under tetthet kurven til venstre for x.

   P{X>x} = e-λx, tilsvarer det området under tetthet kurven til høyre for x.

   P{x1<X≤ x2} = e-λx1 – e-λx2, tilsvarer det området under tetthet kurve mellom x1 og x2.

   Forholdet mellom Distribusjoner

   Forhold mellom Bernoulli, og Binominal Distribusjon

   1., Bernoulli Distribusjon er et spesielt tilfelle av Binomial Fordeling med en enkelt studie.

   2. Det er bare to mulige utfall av en Bernoulli, og Binominal distribusjon, nemlig suksess og fiasko.

   3. Både Bernoulli og Binomiske Fordelinger har egne stier.

   Forhold mellom Poisson og Binominal Distribusjon

   Poisson-Distribusjon er en begrensende tilfelle av binominal distribusjon i henhold til følgende vilkår:

   1. antall forsøk er uendelig stor eller n → ∞.,
   2. sannsynligheten for suksess for hver enkelt studie er samme-og på ubestemt tid liten eller p →0.
   3. np = λ, er endelig.

   Forhold mellom Normal og Binominal Distribusjon & Normal og Poisson-Distribusjon:

   Normal fordeling er en annen begrensende form av binominal distribusjon i henhold til følgende vilkår:

   1. antall forsøk er uendelig stor, n → ∞.
   2. Både p og q er ikke uendelig små.

   normal distribusjon er også en begrensende tilfelle av Poisson-fordeling med parameter λ →∞.,

   Forhold mellom Eksponential-og Poisson-Distribusjon:

   Hvis ganger mellom tilfeldige hendelser følg eksponentiell fordeling med pris λ, så det totale antall hendelser i løpet av lengde t følger Poisson-fordeling med parameter λt.

   Test dine kunnskaper

   Du har kommet så langt. Nå, er du i stand til å svare på følgende spørsmål? Gi meg beskjed i kommentarfeltet nedenfor!

   1. Formelen for å beregne standard normal tilfeldig variabel er:

   en. (x+µ) / σ
   b. (x-µ) / σ
   c. (x-σ) / µ

   2., I Bernoulli Distribusjon, formel for beregning av standardavvik er gitt ved:

   en. p (1 – p)
   b. SQRT(p(p – 1))
   c. SQRT(p(1 – p))

   3. For en normal fordeling, en økning i mellomtiden vil:

   en. skift kurven til venstre
   b. skift kurven til høyre
   c. flat kurve

   4. Levetiden til et batteri er eksponentielt fordelt med λ = 0,05 per time. Sannsynligheten for et batteri til å vare mellom 10 og 15 timer er:

   en.0.1341
   b.0.1540
   c.0.,0079

   Avslutt Notater

   sannsynlighetsfordelinger er utbredt i mange sektorer, nemlig, forsikring, fysikk, ingeniørfag, informatikk og selv samfunnsvitenskap hvor studentene på psykologi og medisinsk er mye ved hjelp av sannsynlighetsfordelinger. Den har en lett påføring og utbredt bruk. Denne artikkelen uthevet seks viktig distribusjoner som er observert i dag-til-dag liv og forklarte sin søknad. Nå vil du være i stand til å identifisere, forholder seg og skille mellom disse distribusjonene.,

   Hvis du er i tvil, og ønsker å se flere artikler om utdelinger, vennligst skriv i kommentarfeltet nedenfor. For en mer dyptgående skrive opp av disse distribusjonene, kan du se denne ressursen.