Madame Lelica

한 것은 우리는 많은 일을 하고 있을 것으로 알고리즘을 이 시리즈에서는 그래프 탐색. 이것이 정확히 무엇을 의미합니까?기본적으로 아이디어는 한 꼭지점에서 다른 꼭지점으로 그래프를 돌아 다니며 상호 연결된 관계의 속성을 발견한다는 것입니다.

두 개의 가장 일반적으로 사용되는 알고리즘 우리가 많이 사용가:깊이 첫 번째 검색(DFS)및 폭 첫 번째 검색(BFS).,

이 두 알고리즘 모두 그래프를 통과 할 수 있지만 다양한 방식으로 다릅니다. DFS 부터 시작합시다.

DFS 는 구현에서”go deep,head first”철학을 활용합니다. 아이디어에서 시작하는 것은 초기 꼭지점(또는 장소),우리는 아래로 이동 경로 중 하나에 도착하기 전까지 끝까지지 않는다면,우리의 목적지에 도달한 다음,우리는 다시 아래로 이동 다른 경로입니다.예를 살펴 보겠습니다., 우리가 있는 방향 그래프는 다음과 같습니다.

이제 아이디어는 우리가 시작에서 꼭짓점 s 고 우리는 발견하게 꼭짓점 t. DFS 를 사용하여,우리가 탐구하는 하나의 경로를 가는 모든 방법을 말하고 찾을 수 없는 경우 t,그 다음 우리는 아래로 이동 다른 경로입니다., 실행한 처리 과정은 다음과 같습니다:

여기 그래서,우리는 아래로 이동 경로(p1)의 첫 번째 이웃 꼭지점과 우리는 그것을 끝이 아니기 때문에 그것은 경로를 향한 다른 정점입니다., 그래서 우리는 아래로 가는 길:

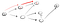
이것은 명확하지 않는 정점을 티 그래서 우리는 다시 이동하기 때문에 우리에 도달했습니다. 이전 노드에는 더 이상 이웃이 없으므로 s 로 돌아갑니다., 에서,우리는 두 번째 이웃 노드:

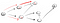
가는 경로를 아래로(p2), 우리는 적어도 여러분에게 세 개의 이웃이 있습니다., 이후 처음으로 한 이미 많이 방문한,우리는 아래로 가야하는 두 번째 중 하나:

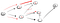
지금 다시 한번 우리는 죽지 않는 정점을 티 그래서 우리는 돌아갑니다., 이 있기 때문에 또 다른 이웃되지 않은 방문,우리는 아래로 이동하는 인접 경로 및 마지막에서 우리는 정점을 티:

이것은 어떻게 DFS 작동합니다. 경로를 내려 가서 목적지 또는 막 다른 골목에 도달 할 때까지 계속 진행하십시오. 그것이 목적지라면,당신은 끝났습니다. 그렇지 않은 경우 돌아가서 해당 경로 내의 모든 옵션을 다 써 버릴 때까지 다른 경로를 계속하십시오.,

우리는 볼 수 있습니다 우리는 동일한 절차에 따라 각 정점에서는 우리가 방문.

할 DFS 에 대한 각각의 이웃의 정점

기 때문이 수반하고 동일한 절차에서,각 단계는 뭔가가 우리에게는 우리가 사용해야 재귀를 구현하는 알고리즘이 있습니다.

여기에는 코드에서 JavaScript:

참고:이 특정 DFS 알고리즘을 확인할 수 있다면 그것은 도달하기 위해 가능한 한 장소에서 다른 장소., DFS 는 다양한 방법으로 사용될 수 있으며 위의 알고리즘에 미묘한 변화가있을 수 있습니다. 그러나 일반적인 개념은 동일하게 유지됩니다.

Dfs 의 분석

이제이 알고리즘을 분석해 보겠습니다. 노드의 각 이웃을 가로 지르며 방문한 것을 무시하고 있기 때문에 o(V+E)의 런타임이 있습니다.

V+E 가 정확히 무엇을 의미하는지에 대한 빠른 설명:

V 는 총 정점 수를 나타냅니다. E 는 총 가장자리 수를 나타냅니다. 모든 꼭지점에는 여러 개의 가장자리가 있습니다.,
v+E 대신 V*E 라고 믿게 될 수도 있지만,V*E 가 정확히 무엇을 의미하는지 생각해 봅시다.

를 위해 뭔가 될 V•E 것을,그것은 의미에 대한 각각의 정점을,우리는 모든 가장자리에서 그래프는지 여부에 관계없이 그리 연결되어 있는 특정 정점입니다.반면에 V+E 는 각 꼭지점에 대해 해당 꼭지점과 관련된 가장자리 수만보고 있음을 의미합니다. 이전 게시물에서 우리가 인접성 목록을 차지하는 공간이 O(V+E)라는 것을 상기하십시오., 각각의 정점의 번호가 있리고 최악의 경우에,우리는 실행하는 DFS 각각에 꼭지점,우리가 수행 O(V)작품과 함께 탐험하는 모든 가장자리의 꼭지점,는 O(E). 일단 모든 V 수의 정점을 살펴보면 총 E 가장자리를 살펴 보았을 것입니다. 따라서,그것은 V+E.

이후,지금 DFS 재귀를 사용하여 각각에 꼭지점,즉 스택을 사용하는(는 이유는 stack overflow error 을 실행할 때마다 무한 귀). 따라서 공간 복잡도는 O(V)입니다.,

이제 폭 우선 검색이 어떻게 다른지 살펴 보겠습니다.

폭 우선 검색

폭 우선 검색(BFS)은”넓은 이동,조감도”철학을 따릅니다. What 는 기본적으로 의미하는 대신 모든 방법 중 하나 아래로 경로 끝날 때까지,BFS 움직임으로 그 대상 중 하나 이웃니다., 무엇인지 살펴 보자는 것을 의미:

하는 것이 더 바람직한 모든 방법은 아래 그것의 첫번째 이웃,BFS 방문하는 모든 이웃의 첫 번째고 다음을 방문하는 그 이웃의 이웃 등에 도달할 때까지 t.,fd17d”>