シンプルな直列回路|直列回路と並列回路|エレクトロニクスの教科書

このページでは、直列回路に関して理解すべき三つの原則について概説します。

電流：直列回路のどの部品でも電流の量は同じです。
抵抗：任意の直列回路の総抵抗は、個々の抵抗の合計に等しいです。Li>
電圧：直列回路の電源電圧は、個々の電圧降下の合計に等しくなります。,li>

これらの原理を示す直列回路の例をいくつか見てみましょう。

私たちは、三つの抵抗と単一のバッテリからなる直列回路から始めましょう：

直列回路について理解するための最初の原則は次のとおりです。

直列回路の電流量は、回路内のどの部品でも同じです。

これは、直列回路に電流が流れるための経路が一つしかないためです。, 電荷はチューブ内のビー玉のような導体を通って流れるので、任意の特定の時点における回路（チューブ）内の任意の時点での流量（大理石の速度）は等しくなければならない。

直列回路におけるオームの法則を用いて

9ボルトのバッテリーを配置する方法から、この回路の電流は時計回りの方向、点1から2から3から4、1に戻って流れることがわかります。しかし、我々は一つの電圧源と三つの抵抗を持っています。ここでオームの法則をどのように使うのですか？,

オームの法則への重要な注意点は、すべての量（電圧、電流、抵抗、および電力）が回路内の同じ二つの点に関して互いに関連しなければならないというこ以下の単一抵抗回路の例では、この概念が実際に動作していることがわかります。,

シンプルな単一抵抗回路でオームの法則を使用して

シングルバッテリー、単一抵抗回路では、回路内の同じ二つの点に適用されるため、簡単に任意の量を計算できます。

ポイント1と2はワイヤと一緒に接続されているため、ポイント3と4のように、ポイント1はポイント2に電気的に共通であり、ポイント3はポイント4に電気的に共通であると言うことができます。, 私たちは9ボルトの起電力を持っていることを知っているので、ポイント1と4の間（バッテリーを横切って直接）、そしてポイント2はポイント1とポイント3とポイント4の間に共通しているので、9ボルトもポイント2と3の間に（抵抗を横切って直接）持たなければならない。したがって、抵抗の両端の電圧（E）とその抵抗の抵抗（R）を知っているので、抵抗を流れる電流にオームの法則（I=E/R）を適用することができます。すべての項（E、I、R）は、回路内の同じ二つの点、その同じ抵抗に適用されるので、予約なしでオームの法則の公式を使用することができます。,

複数の抵抗を持つ回路でオームの法則を使う

複数の抵抗を持つ回路では、オームの法則をどのように適用するかに注意する必要があります。以下の三抵抗の例の回路では、9ボルトが点1と点4の間にあり、これはR1、R2、およびR3の直列組み合わせを介して電流を駆動する起電力の量しかし、9ボルトの値を取り、それを3k、10k、または5k Ωで割って電流値を見つけることはできません。,

9ボルトの数値は回路全体の総量ですが、3k、10k、および5k Ωの数値は個々の抵抗の個々の量です。全電圧の数値を個々の抵抗の数値を持つオームの法則の方程式に差し込むと、結果は実際の回路のどの量とも正確には関係しません。,

R1の場合、オームの法則はR1の抵抗3kΩを与えられたR1の両端の電圧とR1を通る電流の量を関連付けます。

しかし、R1の両端の電圧（三抵抗の直列の組み合わせにわたってバッテリによって供給される合計電圧のみ）を知らず、R1を通る電流を知らないので、どちらの式でも計算できません。 R2とR3についても同じことが言えます：すべての項が回路内の同じ二つの点の間のそれぞれの量を表す場合にのみ、オームの法則の方程式を適用,

だから私たちは何ができますか？私たちは、R1、R2、およびR3の直列組み合わせに印加されるソース（9ボルト）の電圧を知っており、各抵抗の抵抗を知っていますが、これらの量は同じ回路の総抵抗が何であるかを知っていれば、総電圧（I=E/R）の数値で総電流を計算できます。,

複数の抵抗を等価全抵抗に組み合わせる

これは、直列回路の第二の原則に私たちをもたらします：

任意の直列回路の全抵抗は、個々の抵抗の和電流が流れなければならない直列の抵抗が多ければ多いほど、電流が流れにくくなります。,

この問題の例では、直列に3kΩ、10kΩ、および5kΩの抵抗を持ち、合計抵抗は18kΩになります。

本質的に、R1、R2、およびR3を組み合わせた等価抵抗を計算しました。,oltages Using Ohm’S Law

電流が直列回路のすべてのコンポーネントを通って等しいことを知っている（そして、バッテリを通る電流を決定しただけです）、元の回路図に戻り、各コンポーネントを通る電流に注意することができます：

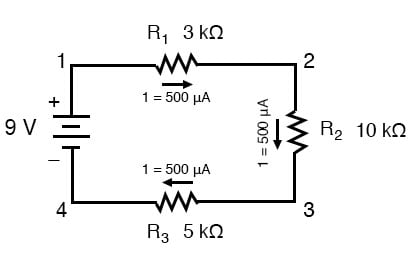
各抵抗を通る電流の量を知っているので、オームの法則を使って各抵抗の電圧降下を決定することができます（適切なコンテキストでオームの法則を適用する）。):

各抵抗の電圧降下と、電圧降下の合計がどのようになるかに注意してください（1。,5 + 5 + 2.5）は電池（供給）電圧と等しいです:9ボルト。

これは直列回路の第三の原則です：

直列回路の電源電圧は、個々の電圧降下の合計に等しい。

“テーブル法”とオームの法則で簡単な直列回路を解析する

しかし、この単純な直列回路を解析するために使用した方法は、より良い理解のために合理化することができます。, 回路内のすべての電圧、電流、および抵抗をリストするテーブルを使用することにより、それらの量のどれがオームの法則の式で適切に関連付けることができるかを非常に簡単に見ることができるようになります。

このようなテーブルのルールは、各垂直列内の値にのみオームの法則を適用することです。たとえば、ER1はIR1およびR1のみ、ER2はIR2およびR2のみなどです。, 最初から与えられたテーブルの要素を入力することによって分析を開始します。

データの配置からわかるように、9ボルトのET（総電圧）をオームの法則の式のいずれかの抵抗（R1、R2、またはR3）に適用することはできません。 9ボルトのバッテリ電圧は、R1、R2、またはR3に直接印加されません。ただし、直列回路の”ルール”を使用して、水平行の空白を埋めることができます。,500μaのt：

次に、電流が直列回路のすべてのコンポーネント（直列回路の別の”ルール”）で等しく共有されていることを知っていると、計算された電流図から各抵抗の電流を埋めることができます。

最後に、オームの法則を使って両端の電圧降下を決定することができます。各抵抗、一度に一つの列：

コンピュータ解析（spice）による計算の検証

楽しみのために、コンピュータを使用してこの非常に同じ回路を自動的, 私たちの計算を検証し、コンピュータ分析にもっと精通する良い方法になります。まず、ソフトウェアによって認識できる形式でコンピュータに回路を記述する必要があります。

使用するSPICEプログラムでは、回路内のすべての電気的に一意の点に番号が付けられ、部品の配置は、それらの番号が付けられた点、つまり”ノード”が共有することによって理解される必要があります。明確にするために、私は私たちの例の回路1から4の四隅に番号を付けました。, しかし、SPICEは回路のどこかにノードゼロがあることを要求しているので、回路を再描画して番号付けスキームを少し変更します。

ここで行ったことは、回路0の左下隅を4ではなく再番号付けすることです。今、私はspiceが理解する言葉で回路を記述するコンピュータファイルに数行のテキストを入力することができます、私たちの視聴の喜びのために電圧と電, このコンピュータファイルはSPICE用語ではネットリストと呼ばれています。

series circuit v1 1 0 r1 1 2 3k r2 2 3 10k r3 3 0 5k .dc v1 9 9 1 .print dc v(1,2) v(2,3) v(3,0) .end

さて、SPICEプログラムを実行してネットリストを処理し、結果を出力するだけです。

v1	v(1,2)	v(2,3)	V(3)	i(v1)
9.000e+00	1.500e+00	5.000e+00	2.500e+00	-5.,000E-04

このプリントアウトは、バッテリ電圧が9ボルトであり、R1、R2、R3の電圧降下がそれぞれ1.5ボルト、5ボルト、2.5ボルトであることを示しています。 SPICEのすべてのコンポーネントの電圧降下は、コンポーネントがその間にあるノード番号によって参照されるため、v(1,2)は回路内のノード1と2の間の電圧を参照しており、これはR1が配置されているポイントです。,

ノード番号の順序は重要です：SPICEがv（1,2）の数値を出力するとき、極性は、ノード1に赤いテストリード、ノード2に黒いテストリードを持つ電圧計を保持している場合と同じように見なされます。また、0.5ミリアンペアまたは500マイクロアンペアの電流（負の値ではあるが）を示すディスプレイもあります。弊社の数理解析していvindicated。この図は、SPICEが現在の計算を処理する方法の癖があるため、SPICE分析では負の数として表示されます。,要約すると、直列回路は、電流が流れることができる一つの経路のみを有するものとして定義される。この定義から、直列回路の三つのルールに従います：すべてのコンポーネントは同じ電流を共有し、抵抗はより大きな総抵抗に等しくなり、電圧降下はより大きな総電圧に等しくなります。これらのルールはすべて、直列回路の定義に根を見つけます。その定義を完全に理解していれば、ルールは定義の脚注に過ぎません。

レビュー：

直列回路内のコンポーネントは同じ電流を共有します：ITotal=I1=I2=。 . ., 直列回路の総抵抗は、個々の抵抗の合計に等しくなります。RTotal=R1+R2+。 . . Rn
直列回路の総電圧は、個々の電圧降下の合計に等しいETotal=E1+E2+。 . . Ja

私たちのツールセクションで私たちのオームの法則の電卓を試してみてください。