そして、あなたはすぐに答え全体を推測しませんでした;代わりに、あなたが分割していた数の”前面”部分(つまり、より大き たとえば、1137を82で割っていた場合、”8″と”10″を見て、おそらく”1″が”11″の上にあるはずだと推測します。8は11に一度フィットするので、おそらく”11″の上にあるはずです。,
多項式の長い除算はほぼ同じように機能します:
まず、除算を設定し、被除数(分割されているもの)を内側と外側と左に置きます。
とりあえず、先行項を過ぎたすべてを無視します。 数値の長い除算と同じように、除数の先頭xと被除数の先頭x2を見ていきます。
先頭のx2を前の先頭のxで割ると、何が得られますか? 私はxを得るだろう。, したがって、xを分割記号の上に置き、x2のすぐ上に置きます。
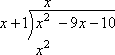
次に、x(上)に1(”側”)を掛け、1xを下に運び、配当の–9xのすぐ下に置きます。
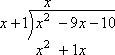
次に、被除数の下に置いたものの下に水平の”等しい”バーを描画しますので、減算を行うことができます。,
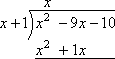
多項式を減算するには、まず第二行のすべての記号を変更します。..
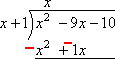
…そして、私はダウン追加します。 最初の項(x2)は(設計上)キャンセルされますが、–9x–1xは–10xになります。
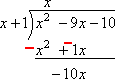
私はその最後の項(つまり、”減算テン”項)を配当から運ぶことを覚えておく必要があります。
この時点で、私は配当を無視し始め、代わりに私の長い部門の一番下の行に取り組んでください。,
私は除数からxを見て、新しい主要な用語、–10xは、除算の一番下の行にあります。 –10xをxで割ると–10になるので、–9xのすぐ上にそれを置きます:
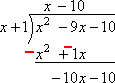
ここで、–10(上)に先頭のx(”側”)を掛け、-10xを前の行の-10xのすぐ下に下に運びます。
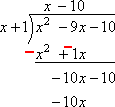
…,そして、-10(上)に1(”側”)を掛け、-10を前の行のすぐ下の-10に運びます。
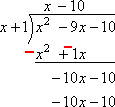
別の水平な”等しい”バーを描画し、下の行のすべての用語の記号を変更します。
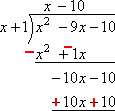
その後、私は追加ダウン:
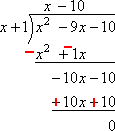
設計により、10xはキャンセルされました。 偶然にも、10のもキャンセルされました。 それから私の答えは、分割記号の上から、次のとおりです。