はじめに
データサイエンスの確率の世界 私は直感的な例で物事をオフに開始してみましょう。
あなたが大学の教師であるとします。 一週間割り当てを確認した後、すべての学生を採点しました。 あなたは大学のデータ入力担当者にこれらの採点された論文を渡し、すべての学生の成績を含むスプレッドシートを作成するように彼に言います。, しかし、その男は成績のみを保存し、対応する学生は保存しません。

彼は別の失態をした、彼は急いでエントリのカップルを逃し、我々は誰の成績が欠落しているのか分かりません。 これを解決する方法を見つけましょう。
一つの方法は、成績を視覚化し、データの傾向を見つけることができるかどうかを確認することです。

プロットしたグラフは、データの頻度分布と呼ばれます。 私たちのデータを定義する構造のような滑らかな曲線があることがわかりますが、異常に気付きますか?, 我々は、特定のスコア範囲で異常に低い周波数を持っています。 したがって、最良の推測は、分布の凹みを取り除く欠損値を持つことです。
これは、データ分析を使用して現実の問題を解決しようとする方法です。 データサイエンティスト、学生、または開業医にとって、分布は概念を知る必要があります。 これは、分析および推論統計の基礎を提供します。
確率の概念は私たちに数学的計算を与えますが、分布は実際にその下で何が起こっているのかを視覚化するのに役立ちます。,
この記事では、明快で包括的な方法で説明されているいくつかの重要な確率分布について説明しました。
注意:この記事では、確率に関する基本的な知識があることを前提としています。 そうでない場合は、この確率分布を参照できます。,
目次
- 一般的なデータ型
- 分布の種類
- ベルヌーイ分布
- 一様分布
- 二項分布
- 正規分布
- ポアソン分布
- 指数分布
- 分布間の関係
- あなたの知識をテスト!
一般的なデータ型
分布の説明に進む前に、どのような種類のデータに遭遇できるかを見てみましょう。 データは、離散的または連続的であり得る。,
離散データは、名前が示すように、指定された値のみを取ることができます。 たとえば、ダイを転がすと、可能な結果は1、2、3、4、5または6であり、1.5または2.45ではありません。
連続データは、指定された範囲内の任意の値を取ることができます。 範囲は有限または無限であり得る。 たとえば、女の子の体重や身長、道路の長さなどです。 女の子の体重は、54kgs、54.5kgs、または54.5436kgsの任意の値にすることができます。
次に、分布のタイプから始めましょう。,
分布の種類
ベルヌーイ分布
ベルヌーイ分布で最も簡単な分布から始めましょう。 それは実際にそれが聞こえるよりも理解しやすいです!
そこにすべてのあなたのクリケット中毒! 任意のクリケットの試合の開始時に、どのようにバットやボールに起こっている人を決めるのですか? トス! それはすべて右、あなたが勝つか負けるかどうかに依存しますか? トスが頭になった場合、あなたが勝つとしましょう。 そうでなければ負ける 途中なんてない。
ベルヌーイ分布は、1(成功)と0(失敗)の二つの可能な結果、および単一の試行のみを持っています。, したがって、ベルヌーイ分布を持つ確率変数Xは、成功の確率で値1、たとえばp、失敗の確率で値0、たとえばqまたは1-pを取ることができます。
ここで、頭の発生は成功を表し、尾の発生は失敗を表します。
頭を得る確率=0.5=尾を得る確率は二つしかありません。p>
確率質量関数は、px(1-p)1-xここでx€(0,1)で与えられます。,
それはまた、として書くことができます
![]()
成功と失敗の確率は、私とアンダーテイカーの間の戦いの結果のように、等しく可能性が高い必要はありません。 彼は勝つことはかなり確実です。 したがって、この場合、私の成功の確率は0.15であり、私の失敗は0.85です
ここで、成功の確率(p)は失敗の確率と同じではありません。 したがって、以下のグラフは、私たちの戦いのベルヌーイ分布を示しています。

ここで、成功確率=0.15、失敗の確率=0.85です。, 期待値はまさにそれが聞こえるものです。 殴ったら殴ってくれるかもしれない 基本的に任意の分布の期待値は分布の平均です。, ベルヌーイ分布からの確率変数Xの期待値は次のように求められます。
E(X)=1*p+0*(1-p)=p
ベルヌーイ分布からの確率変数の分散は次のとおりです。
V(X)=E(X2)–2=p–p2=p(1-p)
ベルヌーイ分布の多くの例は、雨が成功を表し、雨がない場合は失敗を表し、ゲームに勝つ(成功)または負ける(失敗)など、明日に雨が降るかどうかなどです。
一様分布
公正なダイを転がすと、結果は1から6になります。, これらの結果を得る確率は同じように可能性が高く、それが一様分布の基礎です。 ベルヌーイ分布とは異なり、一様分布の可能な結果のすべてのn個は、等しく可能性があります。
変数Xは、密度関数が次のような場合に一様に分布していると言われます。
![]()
一様分布曲線のグラフは次のようになります。

一様分布曲線の形状が長方形であることがわかります。一様分布が矩形分布と呼ばれる理由。,
一様分布の場合、aとbはパラメータです。
花屋で毎日販売される花束の数は、最大40個、最小10個で均一に分布しています。
のは、毎日の売上高が15と30の間に落ちる確率を計算してみましょう。
毎日の売上高が15と30の間に落ちる確率は次のとおりです(30-15)*(1/(40-10)) = 0.5
同様に、毎日の売上が20より大きい確率は=0です。,667
一様分布に従うXの平均と分散は次のとおりです。
Mean->E(X)=(a+b)/2
Variance->V(X)=(b-a)2/12
標準一様密度はパラメータa=0とb=1を持つため、標準一様密度のPDFは次のようになります。:
![]()
二項分布
クリケットに戻りましょう。 あなたが今日トスに勝ったとします。 あなたは再び投げるが、この時間を失った。, 今日トスに勝ったら、これはトスに明日勝つことを必要としない。 あなたがトスに勝った回数に確率変数、たとえばXを割り当ててみましょう。 Xの可能な値は何ですか? それはあなたがコインを投げた回数に応じて任意の数にすることができます。
可能な結果は二つしかありません。 成功を表す頭部および失敗を表す尾。 したがって、ヘッドを得る確率=0.5および失敗の確率は、q=1-p=0.5のように簡単に計算できます。,
成功または失敗、利益または損失、勝または失うなどの二つの結果のみが可能であり、成功と失敗の確率がすべての試行で同じである分布を二項分布と呼ぶ。
結果は同じように可能性がある必要はありません。 私とアンダーテイカーの戦いの例を覚えていますか? したがって、実験の成功確率が0.2であれば、失敗の確率はq=1–0.2=0.8として簡単に計算できます。
前回のトスの結果が現在のトスの結果を決定または影響しないため、各トライアルは独立しています。, 二つの可能な結果のみをn回繰り返した実験は、二項と呼ばれます。 二項分布のパラメーターは、nとpです。nは試行の総数であり、pは各試行の成功確率です。
上記の説明に基づいて、二項分布の特性は
- 各試行は独立である。
- 試験には、成功または失敗のいずれかの二つの可能な結果しかありません。
- n個の同一の試験の総数が実施される。
- 成功と失敗の確率はすべての試行で同じです。, (試験は同じです。,
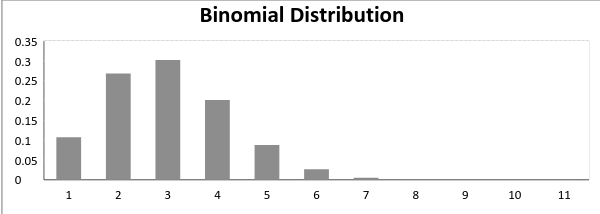
さて、成功の確率=失敗の確率、このような状況では、二項分布のグラフは次のようになります
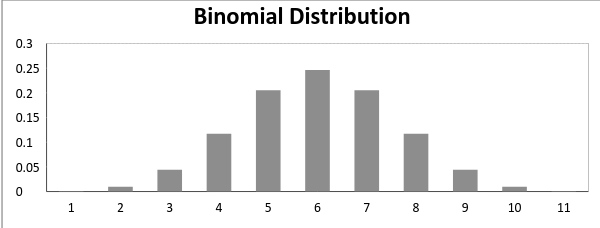
二項分布の平均と分散は次のようになります。
平均->µ=n*p
variance->var(x)=n*p*q
正規分布
正規分布は、宇宙のほとんどの状況の振る舞いを表します(そのため、”正規”分布と呼ばれています。, たぶん!). 大きな(小さな)確率変数の合計は、しばしば正規分布していることが判明し、その広範な適用に貢献します。 任意の分布は、次の特性を持つ場合、正規分布として知られています。
- 分布の平均、中央値、およびモードが一致します。
- 分布の平均、中央値、および
- 分布の曲線は、直線x=∞について鐘形で対称である。
- 曲線の下の総面積は1です。
- 値のちょうど半分は中央の左にあり、残りの半分は右にあります。,
正規分布は二項分布とは大きく異なります。 しかし、試行回数が無限大に近づくと、形状は非常に似ています。
正規分布に従う確率変数XのPDFは、次のように与えられます。

正規分布であると言われる確率変数Xの平均と分散は、次のように与えられます。
Mean->E(X)=μ
Variance-iv id=”aca2d19001″var(X)=σ^2
ここで、μ(平均)とσ(標準偏差)はパラメータです。,
確率変数X~N(μ,μ)のグラフを以下に示す。
標準正規分布は、平均0と標準偏差1の分布として定義されます。 このような場合、PDFは次のようになります。


ポアソン分布
コールセンターで働いているとします。 任意の数にすることができます。 ここで、一日のコールセンターでのコールの総数は、ポアソン分布によってモデル化されます。, いくつかのより多くの例は、一日に病院で記録された緊急コールの数です。
- ある日のエリアで報告された盗難の数。
- 時間でサロンに到着する顧客の数。
- 特定の都市で報告された自殺の数。
- ブックの各ページでの印刷エラーの数。
あなたは今、同じコースに続く多くの例を考えることができます。, ポアソン分布は,事象が時間と空間のランダムな点で発生する状況に適用可能であり,その事象の発生数にのみ関心がある。
次の仮定が有効な場合、分布はポアソン分布と呼ばれます。
1. 成功したイベントは、別の成功したイベントの結果に影響を与えるべきで
2. 短い間隔での成功確率は、長い間隔での成功確率と等しくなければなりません。
3. 区間が小さくなるにつれて、区間での成功確率はゼロに近づきます。,ここで、任意の分布が上記の仮定を検証する場合、それはポアソン分布です。 ポアソン分布で使用されるいくつかの表記法は、
- θはイベントが発生する速度、
- tは時間間隔の長さ、
- Xはその時間間隔におけるイベントの数である。
ここで、Xはポアソン確率変数と呼ばれ、Xの確率分布はポアソン分布と呼ばれます。
μは長さtの区間におけるイベントの平均数を表すとすると、μ=μ*tとなる。,
ポアソン分布に従うXのPMFは、次のように与えられます。

平均μはこの分布のパラメータです。 μは、その区間のμ倍の長さとしても定義されます。 ポアソン分布のグラフを以下に示します。

以下のグラフは、平均の増加による曲線のシフトを示しています。

平均が増加するにつれて、曲線が右にシフトすることが知覚可能である。,
ポアソン分布に従うXの平均と分散:
Mean->E(X)=µ
Variance->Var(X)=µ指数分布
コールセンターの例をもう一度考えてみましょう。 通話間の時間間隔はどうですか? ここでは、指数分布が私たちの救助に来ます。 指数分布は、呼び出し間の時間間隔をモデル化します。
その他の例は次のとおりです。
1. 時間beteeenメトロ到着の長さ、
2。, ガソリンスタンドに到着するまでの時間の長さ
3. エアコンの寿命指数分布は生存解析に広く使用されています。 機械の期待寿命から人間の期待寿命まで、指数分布は結果をうまく提供します。
確率変数Xは、PDFを持つ指数分布を持つと言われています:
f(x)={θe-θx,x≤0
およびパラメータθ>0これはレートとも呼ばれます。,
指数分布に従う確率変数Xの平均と分散:
Mean->E(X)=1/π
分散->var(x)=(1/√)2
また、レートが大きいほど、カーブが速く低下し、レートが低いほど、カーブが平坦になります。 これは、以下のグラフでよりよく説明されています。,
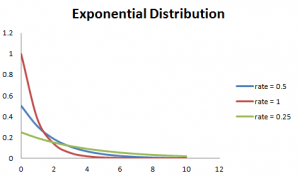
計算を容易にするために、以下のいくつかの式があります。
{X≤x}=1–e-λxに対応する地下の密度曲線の左側にx.
P{X>x}=e-λxに対応する地下の密度曲線の右側にx.
P{x1<X≦x2}=e-λx1–e-λx2に対応する地下の密度曲線でx1、x2.
分布間の関係
ベルヌーイと二項分布の関係
1., ベルヌーイ分布は、単一の試行を伴う二項分布の特殊な場合です。
2. ベルヌーイ分布と二項分布、すなわち成功と失敗の二つの可能な結果しかありません。
3. ベルヌーイ分布と二項分布はどちらも独立した軌跡を持ちます。
ポアソン分布と二項分布の関係
ポアソン分布は、次の条件下での二項分布の限定的なケースです。
- 試行回数が無期限に大きいか、n→∞です。,
- 各試行の成功確率は同じで無期限に小さいかp→0です。
- np=∞は有限です。
正規分布と二項分布の関係&正規分布とポアソン分布:
正規分布は、次の条件下での二項分布の別の制限形式です。
- 試行回数は無期限に大きく、n→∞です。
- pとqの両方が無限に小さくなるわけではありません。
正規分布は、パラメータπ→πを持つポアソン分布の限定的な場合でもあります。,
指数分布とポアソン分布の関係:
ランダムイベント間の時間がレートθを持つ指数分布に従う場合、長さtの期間内のイベントの総数はパラメータθtを持つポアソン分布に従います。
あなたの知識をテストします
あなたはここまで来ました。 さて、あなたは次の質問に答えることができますか? 私は以下のコメントで知ってみましょう!
1. 標準正規確率変数を計算する式は次のとおりです。
a.(x+μ)/λ
b.(x-μ)/λ
c.(x-μ)/μ2., ベルヌーイ分布では、標準偏差を計算するための式は次のように与えられます。
a.p(1-p)
b.SQRT(p(p-1))
c.SQRT(p(1-p))3. 正規分布の場合、平均の増加は次のようになります。
a.曲線を左にシフト
b.曲線を右にシフト
c.曲線を平ten化4. バッテリーの寿命は、λ=0.05/時間で指数関数的に分布しています。 バッテリーが10-15時間持続する確率は次のとおりです。
a.0.1341
b.0.1540
c.0。,0079エンドノート
確率分布は、多くの分野、すなわち、保険、物理学、工学、コンピュータサイエンス、さらには社会科学で流行しており、心理学や医学の学生は広く確率分布を使用しています。 それは容易な適用および広まった使用を有する。 ここでは,日常生活において観察される六つの重要な分布を強調し,その応用について説明した。 これで、これらの分布を識別、関連付け、区別することができます。,
あなたが疑問を持っていると分布に関するより多くの記事を見たい場合は、以下のコメントセクションに書いてください。 これらのディストリビューションの詳細な書き込みについては、このリソースを参照できま
- 分布の平均、中央値、およびモードが一致します。