By Leave a Comment on グラフ上のアルゴリズム：深さ優先探索（DFS）と幅優先探索（BFS）について話しましょう

このシリーズのアルゴリズムで多くのことを行うことの一つ これは正確にどういう意味ですか？

基本的に、アイデアは、ある頂点から別の頂点にグラフの周りを移動し、それらの相互接続された関係の特性を発見するということです。

最も一般的に使用されるアルゴリズムの二つは、深さ優先検索（DFS）と幅優先検索（BFS）です。,

どちらのこれらのアルゴリズムをトラバースグラフなどが異なる異なる。 DFSから始めましょう。

DFSは、その実装において”深く、頭を最初に行く”という哲学を利用しています。 アイデアは、最初の頂点（または場所）から始めて、終わりに達するまで一つの道を下り、目的地に到達しなければ、戻って別の道を下るということです。

例を見てみましょう。, このような有向グラフがあるとします。

dfsを使用して、あるパスを探索し、最後までずっと行き、tが見つからない場合は別のパスを下ります。, プロセスは次のとおりです。

最初の隣接する頂点のパスを下っていく

ここでは、最初の隣接する頂点のパス（p1）を下り、別の頂点に向かうパスがあるため、それが終わりではないことがわかります。, だから私たちはそのパスを下って行く：

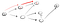
これは明らかに頂点ではありませんtだから我々は行き止まりに達したので、我々は戻らなければならない。 前のノードにはもう隣人がいないので、sに戻ります。, Sから、我々はその第二の隣接ノードに移動します：

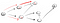
パス（p2）を下って行くと、私たちは三つの隣人に直面しています。, P>

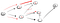
これはdfsがどのように動作するかです。 道を下り、行先か行き止まりに達したまで行き続けなさい。 それが目的地なら、あなたは終わりです。 そうでない場合は、戻って、そのパス内のすべてのオプションを使い果たすまで別のパスを続けてください。,

訪問する各頂点で同じ手順に従っていることがわかります。

頂点の各隣接に対してDFSを実行します

これは各ステップで同じ手順を実行する必要があるため、このアルゴリズムを実装するために再帰を使用する必要があることがわかります。

JavaScriptのコードは次のとおりです。

注：この特定のDFSアルゴリズムにより、ある場所から別の場所に到達できるかどうかを判断できます。, DFSはさまざまな方法で使用でき、上記のアルゴリズムに微妙な変更がある場合があります。 しかし、一般的な概念は同じままです。

DFSの分析

では、このアルゴリズムを分析しましょう。 ノードの各隣接ノードを通過し、訪問したノードを無視しているので、o（V+E）のランタイムがあります。

V+Eが何を意味するのかを簡単に説明します。

Vは頂点の総数を表します。 Eは、エッジの総数を表します。 すべての頂点には多数のエッジがあります。,
V+EではなくV•Eであると信じさせられるかもしれませんが、V•Eが正確に何を意味するのかを考えてみましょう。

何かがV•Eであるためには、各頂点について、それらの辺がその特定の頂点に接続されているかどうかにかかわらず、グラフ内のすべての辺を調べなければならないことを意味します。一方、V+Eは各頂点について、その頂点に関連するエッジの数のみを調べることを意味します。 前回の投稿から、隣接リストに取り上げるスペースはO（V+E）であることを思い出してください。, 各頂点にはいくつかのエッジがあり、最悪の場合、各頂点でDFSを実行する場合、頂点のすべてのエッジ、つまりO（E）を探索するとともにO（V）作業を行 すべてのv個の頂点を見たら、合計E辺も見ていたでしょう。 したがって、それはV+Eです。

DFSは各頂点で再帰を使用するため、スタックが使用されることを意味します（無限再帰呼び出しに実行するたびにスタックオーバーフローエラーと呼ばれる理由です）。 したがって、空間の複雑さはO（V）です。,

次に、幅優先検索の違いを見てみましょう。

幅優先検索

幅優先検索（BFS）は、”広く、鳥瞰図に移動する”という哲学に従っています。 それが基本的に意味することは、bfsが最後まで一つの道を下って行くのではなく、一度に目的地の隣人に向かって移動するということです。, それが何を意味するのかを見てみましょう：

前と同じグラフ

だから、最初の隣人をすべて下って行くのではなく、bfsは最初にsのすべての隣人を訪問し、次にtに達するまでそれらの隣人の,fd17d”>

it looks at its neighbors

then it looks at its neighbors’ neighbors

then finally finds t

See how different DFS and BFS behave?, 私はDFSが頭を上げるのが好きだと思うのが好きですが、BFSはそれをゆっくりと見て、すべてを一歩一歩観察するのが好きです。

今、私たちに際立っている一つの質問は次のとおりでなければなりません：”どの隣人がsの隣人から最初に訪問するかをどのように知るのですか？”

さて、キューのfirst-in-first-out（FIFO）プロパティを利用して、キューの最初の頂点をポップし、その未訪問の隣人をキューに追加し、キューが空になるか、追加した頂点が探していた頂点になるまでこのプロセスを続けることができます。,

JavaScriptのコードを見てみましょう。

BFSの分析

BFSが遅いように見えるかもしれません。 しかし、BFSとDFSの両方の視覚化を注意深く見ると、実際には同じランタイムを持っていることがわかります。

キューは、最大ですべての頂点が宛先に到達するまで処理されることを保証します。 つまり、最悪の場合、BFSはすべての頂点とすべてのエッジも調べます。,

BFSは遅く見えるかもしれませんが、より大きなグラフに実装すると、DFSは最終的に間違っている長い道をたどるのに多くの時間を無駄にすることがわかるので、実際にはより速く見なされます。 実際、BFSはある頂点から別の頂点への最短経路を決定するためのアルゴリズムでよく使用されますが、これらについては後で触れます。したがって、ランタイムは同じであるため、BFSのランタイムはO（V+E）であり、最大V頂点を保持できるキューを使用するため、スペースの複雑さはO（V）です。,

との類似

私は個人的にDFSとBFSがどのように機能するかを想像する他の方法であなたを残したいと思います。

DFSを考えるときはいつでも、多くの行き止まりにぶつかることによって正しい道を見つけるものを考えるのが好きです。 通常、これは食べ物を探すために迷路を通過するネズミのようになります。,p>

これは、プロセスの簡略化されたバージョンがどのように見えるかです：