Una cosa che faremo molto con gli algoritmi di questa serie è graph traversal. Cosa significa esattamente?
Fondamentalmente, l’idea è che ci muoveremo attorno al grafico da un vertice all’altro e scopriremo le proprietà delle loro relazioni interconnesse.
Due degli algoritmi più comunemente usati che useremo molto sono: Depth-First Search (DFS) e Width-First Search (BFS).,
Mentre entrambi questi algoritmi ci permettono di attraversare i grafici, differiscono in modi diversi. Iniziamo con DFS.
DFS utilizza la filosofia “go deep, head first” nella sua implementazione. L’idea è che partendo da un vertice (o luogo) iniziale, percorriamo un percorso fino a raggiungere la fine e se non raggiungiamo la nostra destinazione, torniamo indietro e percorriamo un percorso diverso.
Diamo un’occhiata ad un esempio., Supponiamo di avere un grafo orientato che assomiglia a questo:

Ora l’idea è quella di avviare al vertice s e abbiamo chiesto di trovare vertice t. Utilizzo di DFS, stiamo andando a esplorare un percorso, percorrere tutta la strada fino alla fine e se non troviamo t, poi si scende un altro percorso., Ecco il procedimento:

Quindi, qui, andiamo giù per il sentiero (p1) del primo vicine vertice e vediamo che non è la fine, perché ha un percorso verso un altro vertice., Quindi andiamo giù quel percorso:
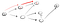
Questo è, chiaramente, il vertice t quindi dobbiamo tornare indietro perché abbiamo raggiunto un punto morto. Poiché il nodo precedente non ha più vicini, torniamo a s., Da s, andiamo al secondo nodo adiacente:
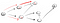
Andare giù per il sentiero (p2), siamo di fronte a tre vicini di casa., Dal momento che il primo è già stato visitato, dobbiamo andare giù per la seconda:
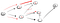
Ora, ancora una volta abbiamo raggiunto un vicolo cieco, che non è il vertice t quindi dobbiamo tornare indietro., Poiché non c’è un altro vicino di casa che non è stato visitato, andiamo giù che vicini percorso e alla fine abbiamo trovato il vertice t:

Questo è come DFS opere. Scendere un sentiero e andare avanti fino a quando hai raggiunto la destinazione o un vicolo cieco. Se è la destinazione, il gioco è fatto. Se non lo è, torna indietro e continua su un percorso diverso finché non hai esaurito tutte le opzioni all’interno di quel percorso.,
Possiamo vedere che seguiamo la stessa procedura per ogni vertice che si visita:
Effettuare una directory per ogni prossimo, del vertice
Dal momento che questo comporta, facendo la stessa procedura, ad ogni passo, qualcosa ci dice che abbiamo la necessità di utilizzare la ricorsione per implementare questo algoritmo.
Ecco il codice in JavaScript:
Nota: Questo specifico algoritmo DFS ci permette di determinare se è possibile arrivare da un posto all’altro., DFS può essere utilizzato in una varietà di modi e ci possono essere sottili modifiche all’algoritmo di cui sopra. Tuttavia il concetto generale rimane lo stesso.
Analisi di DFS
Ora analizziamo questo algoritmo. Poiché stiamo attraversando ogni vicino del nodo e stiamo ignorando quelli visitati, abbiamo un runtime di O(V + E).
Una rapida spiegazione di esattamente cosa significa V+E:
V rappresenta il numero totale di vertici. E rappresenta il numero totale di bordi. Ogni vertice ha un numero di spigoli.,
Mentre può sembrare che si possa essere portati a credere che sia V•E invece di V + E, pensiamo a cosa significa esattamente V•E.Perché qualcosa sia V•E, significherebbe che per ogni vertice, dobbiamo guardare tutti i bordi del grafico indipendentemente dal fatto che quei bordi siano collegati o meno a quel vertice specifico.
Mentre, d’altra parte, V + E significa che per ogni vertice, guardiamo solo il numero di spigoli che riguardano quel vertice. Ricordiamo dal post precedente, che lo spazio che occupiamo per la lista adiacenze è O (V + E)., Ogni vertice ha un numero di bordi e nel peggiore dei casi, se dovessimo eseguire DFS su ogni vertice, avremmo fatto O(V) lavorare insieme ad esplorare tutti i bordi dei vertici, che è O(E). Una volta che abbiamo esaminato tutto il numero V di vertici, avremmo anche esaminato un totale di spigoli E. Pertanto, è V + E.
Ora, poiché DFS utilizza la ricorsione su ciascun vertice, ciò significa che viene utilizzato uno stack (motivo per cui viene chiamato errore di overflow dello stack ogni volta che si esegue una chiamata ricorsiva infinita). Pertanto, la complessità dello spazio è O (V).,
Ora vediamo come differisce la ricerca di ampiezza prima.
Breadth-First Search
Breadth-First Search (BFS) segue la filosofia “go wide, bird’s eye-view”. Ciò che significa fondamentalmente è che invece di andare fino in fondo fino alla fine, BFS si sposta verso la sua destinazione un vicino alla volta., Vediamo cosa significa questo:

per cui invece di andare tutto il senso giù il suo primo del prossimo, BFS vorresti visitare tutti i vicini di casa e poi visitare i vicini di casa vicini di casa e così via fino a quando non raggiunge t.,fd17d”> 

See how different DFS and BFS behave?, Mentre mi piace pensare che a DFS piaccia andare a testa alta, a BFS piace guardare con calma e osservare tutto un passo alla volta.
Ora una domanda che spicca per noi dovrebbe essere: “Come facciamo a sapere quali vicini visitare prima dai vicini di s?”
Bene, potremmo utilizzare la proprietà first-in-first-out (FIFO) di una coda in cui inseriamo il primo vertice della coda, aggiungiamo i suoi vicini non visitati alla coda, e quindi continuiamo questo processo fino a quando la coda è vuota o il vertice che aggiungiamo è il vertice che stavamo cercando.,
Ora diamo un’occhiata al codice in JavaScript:
Analisi di BFS
Potrebbe sembrare che BFS sia più lento. Ma se guardi attentamente le visualizzazioni di BFS e DFS, scoprirai che in realtà hanno lo stesso runtime.
La coda assicura che al massimo ogni vertice verrà elaborato fino a raggiungere la destinazione. Ciò significa che nel peggiore dei casi, BFS guarderà anche tutti i vertici e tutti i bordi.,
Mentre BFS può sembrare più lento, in realtà è considerato più veloce perché se dovessimo implementarli su grafici più grandi, scoprirai che DFS spreca molto tempo percorrendo lunghi percorsi che alla fine sono sbagliati. In effetti, BFS è spesso usato negli algoritmi per determinare il percorso più breve da un vertice all’altro, ma li toccheremo in seguito.
Quindi, poiché i runtime sono gli stessi, BFS ha un runtime di O(V + E) e grazie all’uso di una coda che può contenere al massimo V vertici, ha una complessità dello spazio di O(V).,
Analogie da lasciare con
Voglio lasciarti fuori con altri modi che personalmente immagino come funzionano DFS e BFS nella speranza che ti aiuti a ricordare pure.
Ogni volta che penso a DFS, mi piace pensare a qualcosa che trova la strada giusta urtando in un sacco di vicoli ciechi. Di solito, questo sarebbe come un topo che attraversa un labirinto per cercare cibo.,vorresti provare un percorso, scoprire che la strada è un vicolo cieco, quindi ruotare in un altro percorso e ripetere questo processo fino a quando non raggiunge il suo obiettivo:

E questo è ciò che è una versione semplificata del processo è simile:

Ora per BFS, Ho sempre immaginato come un ripple.,div>

proprio come la BFS inizia alla fonte e visite origine vicini di prima e quindi va più verso l’esterno, visitando i loro vicini di casa e così via:

Riepilogo
- Ricerca Prima di Profondità (DFS) e Breadth-First Search (BFS) sono entrambi utilizzati per attraversare grafici.,
- DFS carica lungo un percorso fino a quando non ha esaurito quel percorso per trovare il suo bersaglio, mentre BFS increspa attraverso i vertici vicini per trovare il suo bersaglio.
- DFS usa uno stack mentre BFS usa una coda.
- Sia DFS che BFS hanno un runtime di O(V + E) e una complessità spaziale di O(V).
- Entrambi gli algoritmi hanno filosofie diverse ma condividono la stessa importanza nel modo in cui attraversiamo i grafici.