Distribuzione di probabilità / Tipi di distribuzioni

Introduzione

Benvenuti nel mondo della probabilità nella scienza dei dati! Permettetemi di iniziare le cose con un esempio intuitivo.

Supponiamo che tu sia un insegnante in un’università. Dopo aver controllato i compiti per una settimana, hai classificato tutti gli studenti. Hai dato questi documenti graduati a un ragazzo di inserimento dati all’università e gli hai detto di creare un foglio di calcolo contenente i voti di tutti gli studenti., Ma il ragazzo memorizza solo i voti e non gli studenti corrispondenti.

Ha fatto un altro errore, ha perso un paio di voci in fretta e non abbiamo idea di chi siano i voti mancanti. Troviamo un modo per risolvere questo problema.

Un modo è visualizzare i voti e vedere se è possibile trovare una tendenza nei dati.

Il grafico che hai tracciato è chiamato la distribuzione di frequenza dei dati. Vedete che c’è una curva liscia come la struttura che definisce i nostri dati, ma notate un’anomalia?, Abbiamo una frequenza anormalmente bassa in un particolare intervallo di punteggio. Quindi la migliore ipotesi sarebbe quella di avere valori mancanti che rimuovano l’ammaccatura nella distribuzione.

Questo è il modo in cui proveresti a risolvere un problema reale usando l’analisi dei dati. Per qualsiasi scienziato di dati, uno studente o un professionista, la distribuzione è un concetto deve sapere. Fornisce la base per l’analisi e le statistiche inferenziali.

Mentre il concetto di probabilità ci dà i calcoli matematici, le distribuzioni ci aiutano a visualizzare effettivamente ciò che sta accadendo sotto.,

In questo articolo, ho trattato alcune importanti distribuzioni di probabilità che sono spiegate in modo lucido e completo.

Nota: Questo articolo presuppone che tu abbia una conoscenza di base della probabilità. In caso contrario, è possibile fare riferimento a questa distribuzioni di probabilità.,

Sommario

Comuni Tipi di Dati
Tipi di Distribuzioni
1. una Distribuzione di Bernoulli
2. Distribuzione Uniforme
3. Distribuzione Binomiale
4. Distribuzione Normale
5. Distribuzione di Poisson
6. Distribuzione Esponenziale
le Relazioni tra le Distribuzioni
Prova la tua Conoscenza!

Tipi di dati comuni

Prima di passare alla spiegazione delle distribuzioni, vediamo che tipo di dati possiamo incontrare. I dati possono essere discreti o continui.,

I dati discreti, come suggerisce il nome, possono assumere solo valori specificati. Ad esempio, quando si tira un dado, i possibili risultati sono 1, 2, 3, 4, 5 o 6 e non 1.5 o 2.45.

I dati continui possono assumere qualsiasi valore all’interno di un determinato intervallo. L’intervallo può essere finito o infinito. Ad esempio, il peso o l’altezza di una ragazza, la lunghezza della strada. Il peso di una ragazza può essere qualsiasi valore da 54 kg, o 54,5 kg, o 54,5436 kg.

Ora iniziamo con i tipi di distribuzioni.,

Tipi di distribuzioni

Distribuzione di Bernoulli

Iniziamo con la distribuzione più semplice che è la distribuzione di Bernoulli. In realtà è più facile da capire di quanto sembri!

Tutti voi drogati di cricket là fuori! All’inizio di qualsiasi partita di cricket, come si fa a decidere chi sta per battere o palla? Un lancio! Tutto dipende se si vince o si perde il lancio, giusto? Diciamo che se il lancio si traduce in una testa, si vince. Altrimenti, perdi. Non c’è una via di mezzo.

Una distribuzione di Bernoulli ha solo due possibili risultati, vale a dire 1 (successo) e 0 (fallimento), e una singola prova., Quindi la variabile casuale X che ha una distribuzione di Bernoulli può assumere il valore 1 con la probabilità di successo, ad esempio p, e il valore 0 con la probabilità di fallimento, ad esempio q o 1-p.

Qui, il verificarsi di una testa indica il successo e il verificarsi di una coda indica il fallimento.
Probabilità di ottenere una testa = 0.5 = Probabilità di ottenere una coda poiché ci sono solo due possibili risultati.

La funzione di massa di probabilità è data da: px(1-p)1-x dove x € (0, 1).,
Può anche essere scritto come

Le probabilità di successo e fallimento non devono essere ugualmente probabili, come il risultato di una lotta tra me e Undertaker. Lui è praticamente certo di vincere. Quindi in questo caso la probabilità del mio successo è 0.15 mentre il mio fallimento è 0.85

Qui, la probabilità di successo(p) non è la stessa della probabilità di fallimento. Quindi, il grafico qui sotto mostra la distribuzione di Bernoulli del nostro combattimento.

Qui, la probabilità di successo = 0,15 e la probabilità di fallimento = 0,85., Il valore atteso è esattamente quello che sembra. Se ti do un pugno, mi aspetto che tu mi risponda. Fondamentalmente il valore atteso di qualsiasi distribuzione è la media della distribuzione., Il valore atteso di una variabile casuale X da una distribuzione di Bernoulli è constatato quanto segue:

E(X) = 1*p + 0*(1-p) = p

La varianza di una variabile casuale da una distribuzione di bernoulli:

V(X) = E(X2) – 2 = p – p2 = p(1-p)

Ci sono molti esempi di distribuzione di Bernoulli come se pioverà domani o non, dove la pioggia, denota successo e senza pioggia, denota il fallimento e Vincente (successo) o perdere (non) gioco.

Distribuzione uniforme

Quando si tira un dado equo, i risultati sono da 1 a 6., Le probabilità di ottenere questi risultati sono ugualmente probabili e questa è la base di una distribuzione uniforme. A differenza della distribuzione di Bernoulli, tutto il numero n di possibili risultati di una distribuzione uniforme è ugualmente probabile.

Una variabile X è detto di essere distribuito in modo uniforme se la funzione di densità è:

Il grafico di una distribuzione uniforme curva sembra

Si può vedere che la forma della distribuzione Uniforme della curva è di forma rettangolare, il motivo per cui distribuzione Uniforme è chiamato rettangolare di distribuzione.,

Per una distribuzione uniforme, a e b sono i parametri.

Il numero di mazzi venduti giornalmente in un negozio di fiori è distribuito uniformemente con un massimo di 40 e un minimo di 10.

Proviamo a calcolare la probabilità che le vendite giornaliere scendano tra 15 e 30.

La probabilità che le vendite giornaliere scendano tra il 15 e il 30 è (30-15)*(1/(40-10)) = 0.5

Allo stesso modo, la probabilità che le vendite giornaliere siano superiori a 20 è = 0.,667

la media e La varianza di X segue una distribuzione uniforme è:

Media> E(X) = (a+b)/2

Varianza -> V(X) = (b-a)2/12

standard di densità uniforme con parametri a = 0 e b = 1, in modo che il PDF per l’uniforme standard della densità è data da:

Distribuzione Binomiale

torniamo a grillo. Supponiamo che tu abbia vinto il lancio oggi e questo indica un evento di successo. Si lancia di nuovo, ma hai perso questa volta., Se vinci un lancio oggi, questo non richiede che vincerai il lancio domani. Assegniamo una variabile casuale, diciamo X, al numero di volte che hai vinto il lancio. Quale può essere il possibile valore di X? Può essere qualsiasi numero a seconda del numero di volte che hai lanciato una moneta.

Ci sono solo due possibili risultati. Testa che denota successo e coda che denota fallimento. Pertanto, la probabilità di ottenere una testa = 0,5 e la probabilità di fallimento può essere facilmente calcolata come: q = 1 – p = 0,5.,

Una distribuzione in cui sono possibili solo due risultati, come successo o fallimento, guadagno o perdita, vittoria o perdita e in cui la probabilità di successo e fallimento è la stessa per tutte le prove è chiamata distribuzione binomiale.

I risultati non devono essere ugualmente probabili. Ricordi l’esempio di una lotta tra me e Undertaker? Quindi, se la probabilità di successo in un esperimento è 0.2 allora la probabilità di fallimento può essere facilmente calcolata come q = 1 – 0.2 = 0.8.

Ogni prova è indipendente poiché il risultato del lancio precedente non determina o influenza il risultato del lancio corrente., Un esperimento con solo due possibili risultati ripetuti n numero di volte è chiamato binomiale. I parametri di una distribuzione binomiale sono n e p dove n è il numero totale di prove e p è la probabilità di successo in ogni prova.

Sulla base della spiegazione di cui sopra, le proprietà di una distribuzione binomiale sono

Ogni prova è indipendente.
Ci sono solo due possibili risultati in una prova – un successo o un fallimento.
Viene condotto un numero totale di prove n identiche.
La probabilità di successo e fallimento è la stessa per tutte le prove., (Le prove sono identiche.,

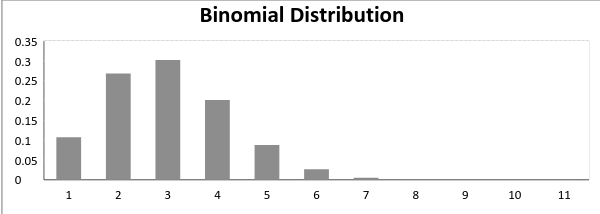
Ora, quando la probabilità di successo = probabilità di guasto, in una tale situazione il grafico della distribuzione binomiale sembra

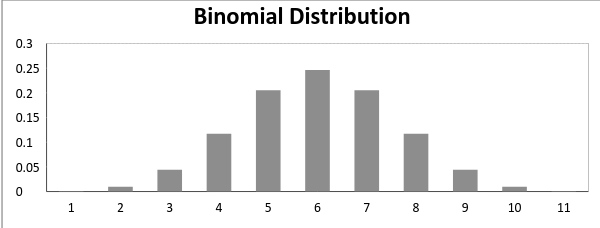
la media e La varianza di una distribuzione binomiale sono date da:

Media> µ = n*p

Varianza -> Var(X) = n*p*q

Distribuzione Normale

distribuzione Normale rappresenta il comportamento della maggior parte delle situazioni nell’universo (Che è il motivo per cui è chiamato una “distribuzione normale”., Credo di si’!). La grande somma di (piccole) variabili casuali spesso risulta essere normalmente distribuita, contribuendo alla sua diffusa applicazione. Qualsiasi distribuzione è nota come distribuzione normale se ha le seguenti caratteristiche:
1. La media, la mediana e la modalità della distribuzione coincidono.
2. La curva della distribuzione è a forma di campana e simmetrica rispetto alla linea x = μ.
3. L’area totale sotto la curva è 1.
4. Esattamente la metà dei valori si trova a sinistra del centro e l’altra metà a destra.,
Una distribuzione normale è molto diversa dalla Distribuzione Binomiale. Tuttavia, se il numero di prove si avvicina all’infinito, le forme saranno abbastanza simili.

Il PDF di una variabile casuale X segue una distribuzione normale è dato da:

la media e La varianza di una variabile casuale X che si dice essere distribuiti normalmente è dato da:

Media> E(X) = µ

Varianza -> Var(X) = s^2

Qui, µ (media) e σ (deviazione standard) sono i parametri.,
Il grafico di una variabile casuale X ~ N (µ, σ) è mostrato di seguito.

Una distribuzione normale standard è definita come la distribuzione con media 0 e deviazione standard 1. In questo caso, il PDF diventa:

Distribuzione di Poisson

Supponiamo di lavorare in un call center, approssimativamente quante chiamate ricevi in un giorno? Può essere qualsiasi numero. Ora, l’intero numero di chiamate in un call center in un giorno è modellato dalla distribuzione di Poisson., Alcuni altri esempi sono
1. Il numero di chiamate di emergenza registrate in un ospedale in un giorno.
2. Il numero di furti segnalati in una zona in un giorno.
3. Il numero di clienti che arrivano in un salone in un’ora.
4. Il numero di suicidi segnalati in una particolare città.
5. Il numero di errori di stampa in ogni pagina del libro.
Ora puoi pensare a molti esempi seguendo lo stesso corso., La distribuzione di Poisson è applicabile in situazioni in cui gli eventi si verificano in punti casuali di tempo e spazio in cui il nostro interesse risiede solo nel numero di eventi dell’evento.

Una distribuzione è chiamata distribuzione di Poisson quando sono valide le seguenti ipotesi:

1. Qualsiasi evento di successo non dovrebbe influenzare l’esito di un altro evento di successo.
2. La probabilità di successo su un breve intervallo deve essere uguale alla probabilità di successo su un intervallo più lungo.
3. La probabilità di successo in un intervallo si avvicina a zero quando l’intervallo diventa più piccolo.,

Ora, se una distribuzione convalida le ipotesi di cui sopra, allora è una distribuzione di Poisson. Alcune notazioni utilizzate nella distribuzione di Poisson sono:
- λ è la velocità con cui si verifica un evento,
- t è la lunghezza di un intervallo di tempo,
- E X è il numero di eventi in quell’intervallo di tempo.
Qui, X è chiamata variabile casuale di Poisson e la distribuzione di probabilità di X è chiamata distribuzione di Poisson.

Sia µ denotare il numero medio di eventi in un intervallo di lunghezza t. Quindi, µ = λ * t.,

Il PMF di X che segue una distribuzione di Poisson è dato da:

Il µ medio è il parametro di questa distribuzione. µ è anche definito come λ volte la lunghezza di tale intervallo. Il grafico di una distribuzione di Poisson è mostrato di seguito:

Il grafico mostrato di seguito illustra lo spostamento della curva dovuto all’aumento della media.

È percepibile che all’aumentare della media, la curva si sposta verso destra.,

la media e La varianza di X segue una distribuzione di Poisson:

Media> E(X) = µ
Varianza -> Var(X) = µ

Distribuzione Esponenziale

si consideri il call center esempio una volta di più. Che dire dell’intervallo di tempo tra le chiamate ? Qui, la distribuzione esponenziale viene in nostro soccorso. La distribuzione esponenziale modella l’intervallo di tempo tra le chiamate.

Altri esempi sono:

1. Lunghezza del tempo beteeen metro arrivi,
2., Periodo di tempo tra gli arrivi in una stazione di servizio
3. La vita di un condizionatore d’aria

Distribuzione esponenziale è ampiamente utilizzato per l’analisi di sopravvivenza. Dalla vita prevista di una macchina alla vita prevista di un essere umano, la distribuzione esponenziale fornisce con successo il risultato.

Si dice che una variabile casuale X abbia una distribuzione esponenziale con PDF:

f(x) = { λe-λx, x ≥ 0

e il parametro λ> 0 che è anche chiamato il tasso.,

Per l’analisi di sopravvivenza, λ è chiamato il tasso di guasto di un dispositivo in qualsiasi momento t, dato che è sopravvissuto fino a t.

Media e Varianza di una variabile casuale X segue una distribuzione esponenziale:

Media> E(X) = 1/λ

Varianza -> Var(X) = (1/λ)2

Inoltre, maggiore è la velocità, più veloce la curva scende e minore è la frequenza, più piatta la curva. Questo è spiegato meglio con il grafico mostrato di seguito.,

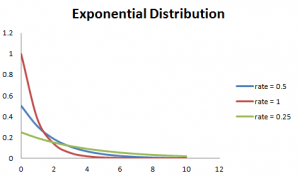
Per facilitare il calcolo, ci sono alcune formule fornite di seguito.
P{X≤x} = 1 – e-λx, corrisponde all’area sotto la curva di densità a sinistra di x.

P{X>x} = e-λx, corrisponde all’area sotto la curva di densità a destra di x.

P{x1<X≤ x2} = e-λx1 – e-λx2, corrisponde all’area sotto la curva di densità tra x1 e x2.

Relazioni tra le distribuzioni

Relazione tra Bernoulli e distribuzione binomiale

1., La distribuzione di Bernoulli è un caso speciale di distribuzione binomiale con una singola prova.

2. Ci sono solo due possibili risultati di una distribuzione Bernoulli e binomiale, vale a dire il successo e il fallimento.

3. Sia Bernoulli che le distribuzioni binomiali hanno percorsi indipendenti.

Relazione tra distribuzione di Poisson e binomiale

La distribuzione di Poisson è un caso limite di distribuzione binomiale nelle seguenti condizioni:
1. Il numero di prove è indefinitamente grande o n → ∞.,
2. La probabilità di successo per ogni prova è la stessa e indefinitamente piccola o p →0.
3. np = λ, è finito.
Relazione tra distribuzione normale e binomiale& Distribuzione normale e Poisson:

La distribuzione normale è un’altra forma limitante della distribuzione binomiale nelle seguenti condizioni:
1. Il numero di prove è indefinitamente grande, n → ∞.
2. Sia p che q non sono indefinitamente piccoli.
La distribuzione normale è anche un caso limite della distribuzione di Poisson con il parametro λ →∞.,

Relazione tra distribuzione esponenziale e Poisson:

Se i tempi tra eventi casuali seguono la distribuzione esponenziale con tasso λ, allora il numero totale di eventi in un periodo di tempo di lunghezza t segue la distribuzione di Poisson con parametro λt.

Metti alla prova le tue conoscenze

Sei arrivato fin qui. Ora, siete in grado di rispondere alle seguenti domande? Fatemi sapere nei commenti qui sotto!

1. La formula per calcolare la variabile casuale normale standard è:

a. (x + µ) / σ
b. (x-µ) / σ
c. (x-σ) / µ

2., Nella distribuzione di Bernoulli, la formula per calcolare la deviazione standard è data da:

a. p(1 – p)
b. SQRT(p(p – 1))
c. SQRT(p (1-p))

3. Per una distribuzione normale, un aumento della media sarà:

a. spostare la curva a sinistra
b. spostare la curva a destra
c.appiattire la curva

4. La durata di una batteria è distribuita esponenzialmente con λ = 0,05 all’ora. La probabilità che una batteria duri tra le 10 e le 15 ore è:

a. 0.1341
b.0.1540
c.0.,0079

Note finali

Distribuzioni di probabilità sono prevalenti in molti settori, vale a dire, assicurazione, fisica, ingegneria, informatica e anche scienze sociali in cui gli studenti di psicologia e medicina sono ampiamente utilizzando distribuzioni di probabilità. Ha una facile applicazione e un uso diffuso. Questo articolo ha evidenziato sei importanti distribuzioni che si osservano nella vita quotidiana e ha spiegato la loro applicazione. Ora sarete in grado di identificare, relazionarsi e differenziare tra queste distribuzioni.,

Se avete dei dubbi e volete vedere altri articoli sulle distribuzioni, si prega di scrivere nella sezione commenti qui sotto. Per una scrittura più approfondita di queste distribuzioni, è possibile fare riferimento a questa risorsa.