egy dolog, hogy mi lesz csinál egy csomó algoritmusok ebben a sorozatban gráf traversal. Mit jelent ez pontosan?
alapvetően az a gondolat, hogy a gráf körül mozogunk egyik csúcsról a másikra, és felfedezzük összekapcsolt kapcsolataik tulajdonságait.
A leggyakrabban használt algoritmusok közül kettő a következő: mélység-első keresés (DFS) és szélesség-első keresés (BFS).,
bár mindkét algoritmus lehetővé teszi számunkra, hogy áthaladjunk a grafikonokon, különböző módon különböznek egymástól. Kezdjük a DFS-vel.
a DFS megvalósításában a “go deep, head first” filozófiát használja. Az ötlet az, hogy egy kezdeti csúcstól (vagy helytől) kezdve egy úton haladunk, amíg el nem érjük a végét, és ha nem érjük el a rendeltetési helyünket, akkor visszatérünk, és más úton megyünk le.
nézzünk egy példát., Tegyük fel, hogy van egy grafikon, ami így néz ki:

Most az ötlet az, hogy elkezdjük a vertex s meg fogjuk kérni, hogy megtalálja vertex t. Használata DFS, felfedezzük egy ösvény, menj végig, hogy a végén, ha nem találunk t, aztán megyünk le egy másik utat., Itt a folyamat:

Szóval itt is van az ösvényen (p1) az első szomszédos csúcs pedig azt látjuk, hogy ez nem a vége, mert van egy felé vezető úton egy újabb csúcs., Szóval így folytatjuk:
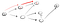
Ez nyilvánvalóan nem a vertex t, így vissza kell mennünk, mert zsákutcába jutottunk. Mivel az előző csomópontnak nincs több szomszédja, visszamegyünk s-be., A s megyünk a második szomszédos csomópont:
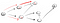
Megy az ösvényen (p2), szembesülünk azzal, hogy három szomszédok., Mivel az első, aki már meglátogatta, le kell mennünk a második:
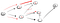
Most, ismét elértük a zsákutca, ami nem a vertex t, így vissza kell mennünk., Mivel van egy másik szomszéd, akit még nem látogattak meg, lemegyünk a szomszédos ösvényen, és végre megtaláltuk a T csúcsot:

így működik a DFS. Menj le egy ösvényen, és menj tovább, amíg el nem éred a célállomást vagy a zsákutcát. Ha ez a cél, végeztél. Ha nem, akkor menj vissza, és folytasd egy másik utat, amíg kimerítette az összes lehetőséget ezen az úton.,
láthatjuk, hogy ugyanazt az eljárást követjük minden meglátogatott csúcson:
készítsen DFS-t a vertex minden szomszédja számára
mivel ez ugyanazt az eljárást vonja maga után minden lépésben, valami azt mondja nekünk, hogy rekurziót kell használnunk az algoritmus végrehajtásához.
itt található a JavaScript kódja:
Megjegyzés: Ez a speciális DFS algoritmus lehetővé teszi számunkra, hogy meghatározzuk, hogy lehetséges-e egy helyről a még egyet., A DFS többféle módon is használható, a fenti algoritmusban pedig finom változások történhetnek. Az általános koncepció azonban változatlan marad.
DFS
elemzése most elemezzük ezt az algoritmust. Mivel a csomópont minden szomszédján áthaladunk, és figyelmen kívül hagyjuk a meglátogatottakat, O(V + E) futási ideje van.
gyors magyarázat arra, hogy pontosan mit jelent a V + E:
V a csúcsok teljes számát jelenti. E az élek teljes számát jelenti. Minden csúcsnak számos éle van.,
bár úgy tűnhet, hogy az ember azt hiheti, hogy V•E A V + E helyett, gondoljunk arra, hogy mit jelent pontosan a V•E.ahhoz, hogy valami V•E legyen, ez azt jelentené, hogy minden egyes csúcsnál meg kell vizsgálnunk a grafikon összes szélét, függetlenül attól, hogy ezek az élek kapcsolódnak-e az adott csúcshoz.
míg viszont a V + E azt jelenti, hogy minden egyes csúcsnál csak az adott csúcshoz tartozó élek számát nézzük. Emlékezzünk vissza az előző bejegyzésből, hogy a szomszédsági listához szükséges hely O (V + E)., Minden csúcsnak számos éle van, és a legrosszabb esetben, ha minden csúcson DFS-t futtatnánk, O(V) munkát végeztünk volna a csúcsok összes szélének feltárásával, ami O(E). Miután megnéztük az összes V csúcsok száma, mi is nézett összesen e élek. Ezért V + E.
most, mivel a DFS minden csúcson rekurziót használ, ez azt jelenti, hogy egy veremet használnak (ezért nevezik verem túlcsordulási hibának, amikor végtelen rekurzív hívásba fut). Ezért a tér összetettsége O (V).,
most nézzük meg, hogyan különbözik a szélesség-első keresés.
Breadth-First Search
Breadth-First Search (BFS) a “GO wide, bird ‘ s eye-view” filozófiát követi. Ez alapvetően azt jelenti, hogy ahelyett, hogy végighaladna egy ösvényen a végéig, a BFS egyszerre egy szomszéd felé halad a rendeltetési hely felé., Nézzük meg, mit jelent ez:

Tehát ahelyett, hogy csak az lesz az első szomszéd, BFS volna, hogy látogassa meg a szomszédok, s az első, majd látogasson el azokat a szomszéd szomszédok, és így tovább, amíg el nem éri t.,fd17d”>


See how different DFS and BFS behave?, Bár szeretem azt hinni, hogy a DFS szeret menni fejét, BFS szeret nézni, hogy lassan, megfigyelni mindent egy lépéssel egy időben.
most egy kérdés, amely kiemelkedik számunkra, a következő: “honnan tudjuk, hogy mely szomszédokat látogatjuk meg először s szomszédaitól?”
Nos, tudtuk kihasználni egy sor first-in-first-out (FIFO) ingatlan, ahol a pop az első csúcs a sorban, hozzá a nem látogatott szomszédok, hogy a sorban, majd folytassa ezt az eljárást, amíg a sor, vagy üres a vertex hozzátesszük, hogy ez a csúcs, amit kerestünk.,
most nézzük meg a kódot a JavaScriptben:
A BFS
elemzése úgy tűnhet, mintha a BFS lassabb lenne. De ha alaposan megnézed mind a BFS, mind a DFS megjelenítését, rájössz, hogy valójában ugyanaz a futási idő.
a sor biztosítja, hogy legfeljebb minden csúcs feldolgozásra kerül, amíg el nem éri a rendeltetési helyet. Ez azt jelenti, hogy a legrosszabb esetben a BFS az összes csúcsot és az összes széleket is megvizsgálja.,
míg a BFS lassabbnak tűnhet, valójában gyorsabbnak tekinthető, mert ha nagyobb grafikonokon hajtanánk végre őket, akkor azt találjuk, hogy a DFS sok időt pazarol hosszú utakra, amelyek végül rosszak. Valójában a BFS-t gyakran használják algoritmusokban, hogy meghatározzák a legrövidebb utat az egyik csúcsról a másikra, de később megérintjük azokat.
Tehát mivel a futásidők azonosak, a BFS-nek O(V + E) futási ideje van, és egy sor használata miatt, amely legfeljebb V csúcsokat képes tartani, O(V) hely összetettsége van.,
analógiák, hogy hagyja ki a
azt akarom, hogy hagyja ki más módon, hogy én személy szerint elképzelni, hogyan működik a DFS és a BFS, abban a reményben, hogy ez segít emlékezni is.
amikor a DFS-re gondolok, szeretek arra gondolni, hogy valami megtalálja a helyes utat, ha sok zsákutcába ütközik. Általában ez olyan lenne, mint egy egér, aki egy labirintuson megy keresztül, hogy élelmet keressen.,megpróbál utat, kiderül, hogy az út zsákutca, akkor fordítsa, hogy egy másik ösvényen, majd ismételje meg ezt a folyamatot, amíg el nem éri a célját:

Ez az, amit egy egyszerűsített változata a folyamat nézne ki:

a BFS, Mindig úgy képzeltem, mint egy hullám.,div>

mint hogy BFS-kor kezdődik a forrást, majd látogatás a forrás szomszédok, aztán megy kifelé ellátogat a szomszédok meg:

Összefoglaló
- Depth-First Search (DFS) széltében-Először Keresés (BFS) mind régen traverse grafikonok.,
- a DFS egy utat tölt fel, amíg kimerítette ezt az utat a cél megtalálásához, míg a BFS a szomszédos csúcsokon keresztül hullámzik, hogy megtalálja a célt.
- a DFS egy köteget használ, míg a BFS egy sort.
- mind a DFS, mind a BFS futási ideje O(V + E), valamint az O(V) tér összetettsége.
- mindkét algoritmusnak különböző filozófiái vannak, de ugyanolyan jelentőséggel bírnak a Grafikonok áthaladásában.