Valószínűségeloszlás / disztribúciók típusai

Bevezetés

Üdvözöljük az Adattudomány valószínűségének világában! Hadd kezdjem el a dolgokat egy intuitív példával.

tegyük fel, hogy egy egyetemi tanár vagy. Miután egy hétig ellenőrizte a feladatokat, osztályozta az összes hallgatót. Odaadtad ezeket a papírokat egy egyetemi adatbeviteli fickónak, és azt mondtad neki, hogy hozzon létre egy táblázatot, amely tartalmazza az összes hallgató osztályzatát., De a srác csak a fokozatokat tárolja, nem pedig a megfelelő hallgatókat.

újabb hibát követett el, sietve kihagyott néhány bejegyzést, és fogalmunk sincs, kinek a jegyei hiányoznak. Találjuk meg a módját, hogy megoldja ezt.

az egyik módja annak, hogy megjelenítse a fokozatok, hátha megtalálja a trend az adatokban.

a grafikon, hogy van telek nevezzük a frekvencia eloszlása az adatok. Látod, hogy van egy sima görbe, mint a szerkezet, amely meghatározza az adatainkat, de észrevesz egy anomáliát?, Rendkívül alacsony frekvenciánk van egy adott ponttartományban. Tehát a legjobb tipp az lenne, ha hiányzó értékek lennének, amelyek eltávolítják a horpadást az eloszlásban.

így próbálna megoldani egy valós problémát az adatelemzés segítségével. Minden adat tudós, egy diák vagy egy orvos, forgalmazás egy kell tudni koncepció. Ez biztosítja az elemzési és következtetési statisztikák alapját.

míg a valószínűség fogalma megadja nekünk a matematikai számításokat, az eloszlások segítenek abban, hogy ténylegesen megjelenítsük, mi történik alatta.,

ebben a cikkben néhány fontos valószínűségi eloszlást fedeztem le, amelyek világos, valamint átfogó módon magyarázhatók.

Megjegyzés: Ez a cikk feltételezi, hogy alapvető ismerete van a valószínűségről. Ha nem, akkor olvassa el ezt a valószínűségi eloszlást.,

Tartalomjegyzék

Közös adattípusok
Típusú Eloszlások
1. Bernoulli Engedély
2. Egyenletes Eloszlás
3. Binomiális Eloszlás
4. Normális Eloszlás
5. Poisson Eloszlás
6. Exponenciális Eloszlás
Kapcsolatok között a Disztribúciók
Tesztelje Tudását!

közös adattípusok

mielőtt folytatnánk a disztribúciók magyarázatát, nézzük meg, milyen adatokkal találkozhatunk. Az adatok lehetnek diszkrét vagy folyamatos.,

A diszkrét adatok, ahogy a neve is sugallja, csak meghatározott értékeket vehetnek fel. Például, ha dobsz egy kockát, a lehetséges eredmények 1, 2, 3, 4, 5 vagy 6, nem pedig 1, 5 vagy 2, 45.

a folyamatos adatok egy adott tartományon belül Bármilyen értéket felvehetnek. A tartomány lehet véges vagy végtelen. Például egy lány súlya vagy magassága, az út hossza. A lány súlya bármilyen érték lehet 54 kg – tól, vagy 54,5 kg – tól, vagy 54,5436 kg-tól.

most kezdjük a disztribúciók típusaival.,

disztribúciók típusai

Bernoulli Eloszlás

kezdjük a legegyszerűbb eloszlással, amely a Bernoulli Eloszlás. Valójában könnyebb megérteni, mint amilyennek hangzik!

minden krikett drogosok odakint! Az elején minden krikett mérkőzés, hogyan dönti el, ki fog denevér vagy labda? Dobás! Minden attól függ, hogy nyersz vagy elveszíted a dobást, igaz? Tegyük fel, hogy ha a dobás fejbe kerül, nyersz. Különben veszítesz. Nincs félút.

a Bernoulli-eloszlásnak csak két lehetséges eredménye van: 1 (siker) és 0 (kudarc), valamint egyetlen próba., Tehát a véletlen változó, X, amely a Bernoulli engedély vehet érték 1 a siker valószínűsége, mondja o, a 0 érték a valószínűsége, hogy a kudarc, mondjuk, k vagy 1-p.

Itt, az esemény, egy fej jelöli siker az esemény egy farok jelöli hiba.
a fej megszerzésének valószínűsége = 0,5 = a farok megszerzésének valószínűsége, mivel csak két lehetséges eredmény létezik.

a valószínűségi tömegfüggvényt a következő adja meg: px(1-p)1-x ahol x € (0, 1).,
azt is meg lehet írni, hogy

a siker és a kudarc valószínűségeinek nem kell ugyanolyan valószínűségeknek lenniük, mint a köztem és Undertaker közötti harc eredménye. Biztos benne, hogy nyer. Tehát ebben az esetben a siker valószínűsége 0,15, míg a kudarcom 0,85

itt a siker valószínűsége (p) nem ugyanaz, mint a kudarc valószínűsége. Tehát az alábbi táblázat mutatja a harcunk Bernoulli eloszlását.

itt a siker valószínűsége = 0,15 és a kudarc valószínűsége = 0,85., A várt érték pontosan az, amit hangzik. Ha megütlek, azt várhatom, hogy visszavágj. Alapvetően várható értéke minden Eloszlás az átlag az eloszlás., A várható érték egy véletlen változó, X a Bernoulli-eloszlást talált a következőképpen:

E(X) = 1*p + 0*(1-p) = p

A variancia egy véletlen változó, a bernoulli-eloszlást:

V(X) = E(X2) – 2 = p – p2 = p(1-p)

sok példa Van, Bernoulli engedély például, hogy esni fog holnap vagy sem, hogy hol az eső jelöli, a siker pedig nem eső jelöli hiba Győztes (siker), vagy elvesztése (hiba) a játék.

egyenletes eloszlás

Ha egy tisztességes die-t forgat,az eredmények 1-6., A valószínűségek szerzés ezek az eredmények egyaránt valószínű, és ez az alapja az egységes Eloszlás. Ellentétben Bernoulli Eloszlás, az összes n lehetséges kimenetelek száma egységes Eloszlás egyformán valószínű.

azt mondják, hogy egy X változó egyenletesen oszlik el, ha a sűrűségfüggvény:

az egységes eloszlási görbe grafikonja úgy néz ki, mint

látható, hogy az egyenletes eloszlási görbe alakja téglalap alakú, ezért az egyenletes eloszlást téglalap alakú eloszlásnak nevezik.,

az egyenletes eloszláshoz az A és b a paraméterek.

a virágüzletben naponta értékesített csokrok száma egyenletesen oszlik el, legfeljebb 40, de legalább 10.

próbáljuk meg kiszámítani annak valószínűségét, hogy a napi értékesítés 15-30 közé esik.

annak a valószínűsége, hogy a napi értékesítés 15-30 közé esik (30-15)*(1/(40-10)) = 0.5

hasonlóképpen, annak a valószínűsége, hogy a napi értékesítés nagyobb, mint 20 = 0.,667

A jelent s eltérést X követően egyenletes eloszlás:

Érted -> E(X) = (a+b)/2

Variancia -> V(X) = (b-a)2/12

Az egyenruha a sűrűség paraméterek a = 0, b = 1, akkor a PDF standard egységes sűrűség által adott:

Binomiális Eloszlás

térjünk vissza a tücsök. Tegyük fel, hogy ma megnyerte a dobást, ami sikeres eseményt jelez. Megint dobsz, de ezúttal vesztettél., Ha nyersz egy dobás ma, ez nem teszi szükségessé, hogy meg fogja nyerni a dobás holnap. Rendeljünk hozzá egy véletlenszerű változót, mondjuk X-et, hogy hányszor nyerted a dobást. Mi lehet az X lehetséges értéke? Ez lehet bármilyen szám attól függően, hogy hányszor dobott egy érmét.

csak két lehetséges kimenetel létezik. A fej a sikert és a farok a kudarcot jelöli. Ezért a fej = 0,5 megszerzésének valószínűsége, valamint a kudarc valószínűsége könnyen kiszámítható: q = 1-p = 0,5.,

olyan Eloszlás, ahol csak két kimenetel lehetséges, például siker vagy kudarc, nyereség vagy veszteség, győzelem vagy veszteség, és ahol a siker és kudarc valószínűsége azonos az összes vizsgálatban, binomiális eloszlásnak nevezzük.

az eredményeknek nem kell egyformán valószínűnek lenniük. Emlékszel a példára, amikor veszekedtünk Undertaker-rel? Tehát, ha a kísérlet sikerének valószínűsége 0,2, akkor a kudarc valószínűsége könnyen kiszámítható q = 1 – 0,2 = 0,8.

minden próba független, mivel az előző dobás eredménye nem határozza meg vagy befolyásolja az aktuális dobás eredményét., Egy kísérlet csak két lehetséges eredmények ismételt n hányszor nevezik binomial. A binomiális eloszlás paraméterei n és p, ahol n a kísérletek teljes száma, és P az egyes próbák sikerességének valószínűsége.

a fenti magyarázat alapján a binomiális eloszlás tulajdonságai

minden próba független.
egy kísérletben csak két lehetséges kimenetel van – akár siker, akár kudarc.
összesen n azonos vizsgálatokat végeznek.
a siker és a kudarc valószínűsége minden kísérlet esetében azonos., (A kísérletek azonosak.,
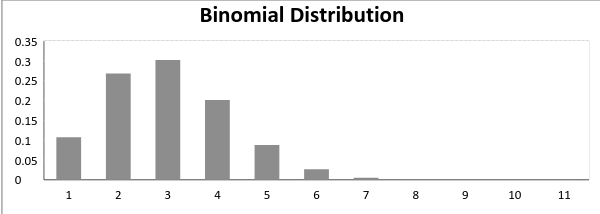
Most, amikor a valószínűsége, hogy a siker = a kudarc valószínűsége, hogy ilyen helyzetben a grafikon a binomiális eloszlás úgy tűnik,

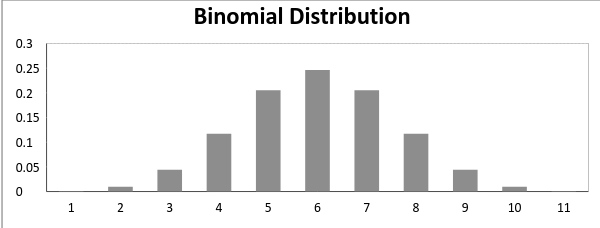
A jelent s eltérés a binomiális eloszlás által adott:

Érted -> μ = n*p

Variancia -> Var(X) = n*p*q

Normális Eloszlás

Normál eloszlás képviseli a viselkedése a legtöbb esetben az univerzumban (ezért hívják a “normális” engedély., Azt hiszem!). A (kis) véletlen változók nagy összege gyakran kiderül, hogy általában eloszlik, hozzájárulva annak széles körű alkalmazásához. Bármely Eloszlás normál eloszlás néven ismert, ha a következő jellemzőkkel rendelkezik:
1. az eloszlás átlagos, medián és módja egybeesik.
2. az eloszlás görbéje harang alakú és szimmetrikus az x = μ vonal körül.
3. a görbe alatti teljes terület 1.
4. az értékek pontosan fele a központ bal oldalán, a másik fele pedig jobbra.,
a normál eloszlás nagyon különbözik a binomiális eloszlástól. Ha azonban a kísérletek száma megközelíti a végtelenséget, akkor az alakzatok meglehetősen hasonlóak lesznek.

A PDF egy véletlen változó X követően normális eloszlás által adott:

Az átlagos várható értékű, egy szórású véletlen változó, X, amelyek azt mondják, hogy normális eloszlású az adott azáltal, hogy:

Érted -> E(X) = μ

Variancia -> Var(X) = σ^2

Itt, μ (átlagos), valamint σ (szórás) a paraméterek.,
egy X ~ N (µ, σ) véletlenszerű változó grafikonja az alábbiakban látható.

a normál eloszlást a 0-as átlaggal és az 1-es szórással rendelkező Eloszlás határozza meg. Ilyen esetben a PDF a következő lesz:

Poisson Distribution

tegyük fel, hogy egy call centerben dolgozik, körülbelül hány hívást kap egy nap alatt? Bármilyen szám lehet. Most, a hívások teljes számát egy call centerben egy nap alatt a Poisson disztribúció modellezi., Néhány további példa a
1. a kórházban egy nap alatt rögzített segélyhívások száma.
2. azon lopások száma, amelyeket egy adott területen egy napon jelentettek.
3. a szalonba érkező ügyfelek száma Egy óra alatt.
4. az adott városban jelentett öngyilkosságok száma.
5. a nyomtatási hibák száma a könyv minden oldalán.
most már sok példára gondolhat ugyanazon tanfolyam után., A Poisson-eloszlás olyan helyzetekben alkalmazható, amikor az események véletlenszerű időpontokban és térben fordulnak elő, ahol érdeklődésünk csak az esemény előfordulásának számában rejlik.

az eloszlást Poisson-eloszlásnak nevezzük, ha a következő feltételezések érvényesek:

1. Minden sikeres esemény nem befolyásolhatja egy másik sikeres esemény eredményét.
2. A siker valószínűsége egy rövid idő alatt meg kell egyeznie a siker valószínűségével egy hosszabb intervallumban.
3. A siker valószínűsége egy intervallumban megközelíti a nullát, mivel az intervallum kisebb lesz.,

most, ha bármely Eloszlás érvényesíti a fenti feltételezéseket, akkor ez egy Poisson eloszlás. A Poisson-eloszlásban használt egyes jelölések a következők:
- λ egy esemény bekövetkezésének sebessége,
- t egy időintervallum hossza,
- és X az adott időintervallum eseményeinek száma.
itt az X-et Poisson Random változónak, az X valószínűségi eloszlását Poisson-eloszlásnak nevezzük.

let µ jelöli az események átlagos számát egy T hosszúságú intervallumban. ezután µ = λ * t.,

a Poisson-eloszlást követő X PMF-je a következő:

Az átlagos µ az eloszlás paramétere. a µ-t ezen intervallum λ-szorosaként is definiáljuk. A Poisson-eloszlás grafikonja az alábbiakban látható:

az alábbi grafikon szemlélteti a görbe eltolódását az átlag növekedése miatt.

észrevehető, hogy az átlag növekedésével a görbe jobbra tolódik.,

Az X átlagos és varianciája Poisson-eloszlás után:

átlag- > E(X) = µ
variancia – > var(X) = µ

exponenciális eloszlás

vegyük még egyszer a Call center példáját. Mi a helyzet a hívások közötti időintervallummal ? Itt az exponenciális eloszlás jön a megmentésünkre. Az exponenciális eloszlás modellezi a hívások közötti időintervallumot.

egyéb példák:

1. Időtartam beteeen metró érkezések,
2., A benzinkúthoz érkezők közötti időtartam
3. Az élet egy légkondicionáló

exponenciális eloszlás széles körben használják a túlélési elemzés. A gép várható élettartamától az emberi várható élettartamig az exponenciális eloszlás sikeresen biztosítja az eredményt.

egy X véletlen változóról azt mondják, hogy exponenciális eloszlása van PDF-vel:

f (x)={λe-λx, x ≥ 0

és λ>0 paraméter, amelyet szintén sebességnek neveznek.,

A túlélés analízis, λ az úgynevezett sikertelen, a készülék bármikor t, tekintve, hogy túlélte fel, hogy a t.

Értem várható értékű, egy szórású véletlen változó X következő exponenciális eloszlás:

Érted -> E(X) = 1/λ

Variancia -> Var(X) = (1/λ)2

Is, minél nagyobb a sebesség, annál gyorsabb a görbe csepp, annál alacsonyabb a ráta, laposabb a görbe. Ezt jobban magyarázza az alábbi grafikon.,

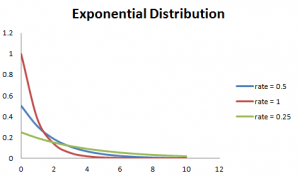
a számítás megkönnyítése érdekében az alábbiakban néhány képlet található.
P{X≤x} = 1 – e-λx, megfelel a területen a sűrűség görbe balra az x-et.

P{X>x} = e-λx, megfelel a területen a sűrűség görbe jobbra az x-et.

P{x1<X≤ x2} = e-λx1 – e-λx2, megfelel a területen a sűrűség görbe közötti x1, illetve x2.

A disztribúciók közötti kapcsolatok

A Bernoulli és a binomiális eloszlás közötti kapcsolat

1., A Bernoulli Eloszlás a binomiális eloszlás egy speciális esete, egyetlen próbával.

2. A Bernoulli és a binomiális eloszlásnak csak két lehetséges kimenetele van: a siker és a kudarc.

3. Mind a Bernoulli, mind a binomiális disztribúciók független nyomvonalakkal rendelkeznek.

A Poisson és a binomiális eloszlás közötti kapcsolat

Poisson eloszlás a binomiális eloszlás korlátozó esete a következő feltételek mellett:
1. a vizsgálatok száma határozatlan ideig nagy vagy n → ∞.,
2. a siker valószínűsége minden kísérlet esetében azonos és határozatlan ideig kicsi vagy p →0.
3. NP = λ, véges.
Kapcsolat Normális, Binomiális Eloszlás & Normális, Poisson Eloszlás:

Normál eloszlás másik korlátozó formában a binomiális eloszlás az alábbi feltételek mellett:
1. A kísérletek számának korlátlanul nagy, n → ∞.
2. mind a P, mind a q nem határozatlan ideig kicsi.
a normál eloszlás szintén a Poisson eloszlás korlátozó esete a λ →∞paraméterrel.,

Kapcsolat Exponenciális, illetve Poisson Eloszlás:

Ha a szer között véletlenszerű események kövesse az exponenciális eloszlás arány λ, akkor az események teljes száma az időszak hossza t követi a Poisson eloszlás paraméter λt.

tesztelje tudását

eddig jöttél. Most, meg tudja válaszolni a következő kérdésekre? Hadd tudja az alábbi megjegyzéseket!

1. A standard normál random változó kiszámításához használt képlet:

A. (x+µ) / σ
b. (x-µ) / σ
c. (x-σ)/µ

2., A Bernoulli eloszlásban a szórás kiszámításának képletét a következők adják:

A. p (1-p)
b. SQRT (p (p-1)))
C. SQRT(p(1 – p))

3. Normál eloszlás esetén az átlag növekedése:

a. tolja a görbét balra
b. tolja a görbét jobbra
c. simítsa a görbét

4. Az akkumulátor élettartama exponenciálisan eloszlik λ = 0,05 óránként. Annak a valószínűsége, hogy egy akkumulátor 10 és 15 óra között tart, a következő:

a.0.1341
b.0.1540
c.0.,0079

végjegyzetek

valószínűségi eloszlások elterjedt számos ágazatban, nevezetesen, biztosítás, fizika, mérnöki, számítástechnika, sőt a társadalomtudomány, ahol a diákok a pszichológia és az orvosi széles körben használják valószínűségi eloszlások. Ez egy egyszerű alkalmazás, széles körben használják. Ez a cikk hat fontos, a mindennapi életben megfigyelhető eloszlást emelt ki, és ismertette azok alkalmazását. Most már képes lesz azonosítani, kapcsolódnak, és különbséget ezek között a disztribúciók.,

ha kétségei vannak, és további cikkeket szeretne látni a disztribúciókról, kérjük, írjon az alábbi megjegyzés szakaszban. Ezen disztribúciók részletesebb leírásához hivatkozhat erre az erőforrásra.