tällä sivulla, me hahmotella kolme periaatetta, sinun pitäisi ymmärtää, koskien sarja circuits:
- Nykyinen: määrä, nykyinen on sama läpi kaikki osa sarjan piiri.
- vastus: minkä tahansa sarjan piirin kokonaisvastus on yhtä suuri kuin yksittäisten vastusten summa.
- Jännite: syöttöjännitteen sarjan piiri on yhtä suuri kuin summa yksittäisten jännite laskee.,
Katsotaanpa joitakin esimerkkejä sarjan piirejä, jotka osoittavat nämä periaatteet.
aloitamme sarjan piiri, joka koostuu kolmesta vastukset ja yhden akun:

ensimmäinen periaate ymmärtää sarjan piirit on seuraava:
määrä nykyisen sarjan piiri on sama kautta tahansa osa piiri.
Tämä johtuu siitä, että sarjapiirin virtaukselle on vain yksi polku., Koska sähkövaraus virtaa johtimia, kuten marmorit putkessa, virtausnopeus (marmori nopeus) missään vaiheessa piiri (putki) milloin tahansa tiettynä ajankohtana on oltava yhtä suuri.
Käyttäen Ohmin Laki, Sarjaan Piirejä
tavalla, että 9 voltin akku on järjestetty, voimme sanoa, että nykyinen piirin virtaa myötäpäivään, alkaen kohta 1 2 3 4 ja takaisin 1. Meillä on kuitenkin yksi jännitteen lähde ja kolme vastusta. Miten käytämme Ohmin lakia?,
merkittävä varoitus Ohmin Laki on, että kaikki suureet (jännite, virta, vastus ja teho) on liityttävä toisiinsa nähden samat kaksi pistettä piiri. Voimme nähdä tämän käsitteen toiminnassa yhden vastus piiri esimerkki alla.,
Käyttäen Ohmin Laki on Yksinkertainen, Yhden Vastuksen Piiri
yhden akun, yhden vastuksen piiri, voimme helposti laskea tahansa määrä, koska ne kaikki levitetään samat kaksi pistettä piiri:


Koska kohdissa 1 ja 2 on kytketty yhteen siten, että lanka vähäinen vastus, koska ovat kohdat 3 ja 4, voimme sanoa, että kohta 1 on sähköisesti yhteisiä vaiheessa 2 ja vaiheessa 3 on sähköisesti yhteisten 4 kohta., Koska me tiedämme, että meillä on 9 volttia sähkömotorinen voima pisteiden välillä 1 ja 4 (vastapäätä akku), ja koska kohta 2 on yhteinen 1 kohta ja 3 kohta yhteinen 4 kohta, meidän on myös 9 voltin pisteiden välillä 2 ja 3 (suoraan koko vastus).
näin Ollen voimme soveltaa Ohmin Laki (I = E/R) nykyinen vastuksen yli, koska tiedämme jännite (E) koko vastus ja vastus (R), että vastus. Kaikki termit (E, i, R) koskevat samoja kahta pistettä piiri, että sama vastus, joten voimme käyttää Ohmin lain kaava ilman varausta.,
Ohmin lain käyttäminen piireissä, joissa on useita vastuksia
piireissä, joissa on useampi kuin yksi vastus, meidän on oltava varovaisia, miten sovellamme Ohmin lakia. Kolmen vastuksen esimerkiksi piirin alla, tiedämme, että meillä on 9 volttia pisteiden välillä 1 ja 4, joka on määrä sähkömotorinen voima ajo nykyinen läpi sarjan yhdistelmä R1, R2 ja R3. Kuitenkin, emme voi ottaa arvo 9 volttia ja jakaa sen 3k, 10k tai 5k Ω yrittää löytää nykyinen arvo, koska emme tiedä, kuinka paljon jännite on yli mitään yksi niistä, resistorit / vastukset, yksilöllisesti.,

luku 9 volttia on yhteensä määrä koko piiri, ottaa huomioon, että luvut 3k, 10k ja 5k Ω ovat yksittäisiä määriä yksittäisiä vastuksia. Jos me plug luku yhteensä jännite osaksi Ohmin Laki, yhtälö, jossa on kuva yksittäisten vastus, tulos ei liity tarkasti tahansa määrä todellinen piiri.,
Varten R1, Ohmin Laki on liittyvät määrä jännite koko R1 nykyisen läpi R1, annettu R1 vastus, 3kΩ:

Mutta, koska emme tiedä, jännite koko R1 (vain yhteensä syöttöjännite akku yli kolme-vastus sarja yhdistelmä) ja emme tiedä, nykyinen kautta R1, emme voi tehdä mitään laskutoimituksia joko kaava. Sama koskee R2 ja R3: voimme soveltaa Ohmin Laki yhtälöt, jos ja vain, jos kaikki ehdot ovat edustavia niiden määrät välillä samat kaksi pistettä piiri.,
so what can we do? Meidän tietää jännite lähde (9 volttia), joita sovelletaan koko sarja yhdistelmä R1, R2 ja R3, ja me tiedämme, että vastus kunkin vastuksen, mutta koska määrät eivät ole samassa yhteydessä, emme voi käyttää Ohmin Laki määrittää virtapiirin virta. Kunpa vain tietäisimme, mikä on piirin kokonaisvastus: sitten voisimme laskea kokonaisvirran kokonaisjännitteelle (I=E/R).,
Yhdistämällä Useita Vastukset osaksi Vastaavaa Yhteensä Vastus
Tämä tuo meidät toinen periaate-sarjan piirit:
koko vastus mikä tahansa sarja piiri on yhtä suuri kuin summa yksittäisten vastusten.
tämän pitäisi olla intuitiivista: mitä enemmän vastuksia sarjassa virran pitää virrata läpi, sitä vaikeampi virran on virrata.,
esimerkissä ongelma, meillä oli 3 kΩ, 10 kΩ, 5 kΩ vastukset sarjassa, antaa meille koko vastus 18 kΩ:

pohjimmiltaan, olemme laskeneet vastaava vastus R1, R2, ja R3 yhdistettynä.,oltages Käyttäen Ohmin Laki
Tietäen, että nykyinen on yhtä suuri läpi kaikki osat sarjan piiri (ja me vain määritetty nykyisen akun avulla), emme voi mennä takaisin meidän alkuperäiseen piiri kaavamaisen ja huomaa, nykyinen kautta jokainen komponentti:
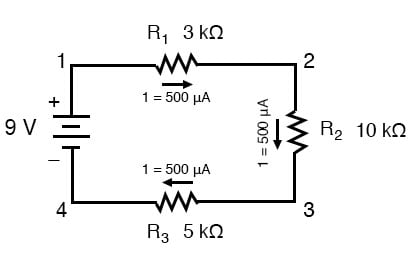
Nyt, kun tiedämme, että määrä virtaa läpi jokaisen vastuksen, voimme käyttää Ohmin Laki määrittää jännitehäviön kukin yhden (soveltamalla Ohmin Laki sen oikeassa yhteydessä):

Huomaa, että jännite laskee koko kunkin vastuksen, ja miten summa jännite laskee (1.,5 + 5 + 2.5) on yhtä suuri kuin akun (syöttö) jännite: 9 volttia.
Tämä on kolmas periaate-sarjan piirit:
syöttöjännite sarjan piiri on yhtä suuri kuin summa yksittäisten jännite laskee.
Analysointi Yksinkertainen Sarja Piirien kanssa ”Taulukko” – Menetelmä ja Ohmin Laki
Kuitenkin, menetelmä, jota käytimme analysoida tämä yksinkertainen sarja piiri voi olla virtaviivainen ymmärtämistä., Käyttämällä taulukko, jossa luetellaan kaikki jännite, virta ja vastus piiri, se on erittäin helppo nähdä, mikä näitä määriä voidaan asianmukaisesti liity millään Ohmin Lain kaavalla:

sääntö, jossa tällainen taulukko on soveltaa Ohmin Lakia vain arvot sisällä jokainen pystysuora sarake. Esimerkiksi, ER1 vain IR1 ja R1; ER2 vain IR2 ja R2; jne., Aloitat analyysi täyttämällä ne elementit taulukko, joka annetaan sinulle alusta alkaen.

Kuten voit nähdä järjestely tietoja, emme voi soveltaa 9 volttia ET (yhteensä jännite) mitään vastusten (R1, R2 tai R3) missään Ohmin Laki kaava, koska ne ovat eri sarakkeissa. Akkujännitteen 9 volttia ei kohdisteta suoraan R1: n, R2: n tai R3: n yli. Sarjapiirien ”säännöillä” voimme kuitenkin täyttää tyhjät kohdat vaakasuoralla rivillä.,t 500 µA:

Sitten, tietäen, että nykyinen on jaettu tasapuolisesti kaikki osat sarjan piiri (toinen ”sääntö” – sarjan piirit), voimme täyttää virtaukset kunkin vastuksen nykyisestä vain lasketaan:

Lopuksi, voimme käyttää Ohmin Laki määrittää jännitehäviön kukin vastus, yksi sarake kerrallaan:

Tarkastaa Laskelmat Tietokone Analyysi (SPICE)
Just for fun, voimme käyttää tietokonetta analysoida tämä sama piiri automaattisesti., Se on hyvä tapa tarkistaa laskelmamme ja myös perehtyä tietokoneanalyysiin. Ensinnäkin meidän on kuvattava piiri tietokoneeseen muodossa tunnistettavissa ohjelmisto.
SPICE ohjelma käytämme edellyttää, että kaikki sähköisesti ainutlaatuinen pistettä piiri on numeroitu, ja komponenttien sijoittelu on ymmärtää, mikä niistä numeroitu pisteitä, tai ”solmut”, he kertovat. Selvyyden vuoksi numeroin esimerkkipiirimme neljä kulmaa 1: stä 4: ään., SPICE, kuitenkin, edellyttää, että on olemassa solmu nolla jossain piiri, niin voin piirtää piiri, muuttaa numerointia hieman:

Kaikki olen tehnyt täällä on uudelleen-numeroitu vasemmassa alakulmassa piiri 0 sijasta 4. Nyt, en voi syöttää useita rivejä tekstiä tietokoneen tiedosto, jossa kuvataan piirin osalta SPICE ymmärtää, täydellinen pari ylimääräistä riviä koodia ohjaa ohjelman näyttö jännite ja virta tiedot meidän katselu ilo., Tämä tiedosto tietokoneella, tunnetaan netlist vuonna SPICE käsitteet:
series circuit v1 1 0 r1 1 2 3k r2 2 3 10k r3 3 0 5k .dc v1 9 9 1 .print dc v(1,2) v(2,3) v(3,0) .end
Nyt, kaikki minun täytyy tehdä on ajaa SPICE ohjelma käsitellä netlist ja lähdön tulokset:
| v1 | v(1,2) | v(2,3) | v(3) | – i(v1) |
|---|---|---|---|---|
| 9.000 E+00 | 1.500 E+00 | 5.000 E+00 | 2.500 E+00 | -5.,000E-04 |
Tämä tuloste kertoo meille, akun jännite on 9 volttia, ja jännite laskee koko R1, R2 ja R3 ovat 1,5 volttia, 5 volttia ja 2.5 volttia, vastaavasti. Jännite laskee koko tahansa osa SPICE viittaa solmun numerot komponentin välissä, niin v(1,2) on linkitykset välinen jännite solmut 1 ja 2 piiri, jotka ovat pisteitä, joiden välillä R1 sijaitsee.,
jotta solmu numerot on tärkeää: kun SPICE lähdöt luku v(1,2), se tulee napaisuuden samalla tavalla kuin jos olimme tilalla volttimittari punainen testi johtaa solmun 1 ja musta testi johtaa solmun 2. Meillä on myös näyttö, joka näyttää virran (vaikkakin negatiivisella arvolla) 0,5 milliampeerissa tai 500 mikroampeerissa. Tietokone on siis todistanut matemaattisen analyysimme oikeaksi. Tämä luku näkyy negatiivisena numerona, MAUSTE-analyysi, johtuen oikku tavalla SPICE kahvat nykyiset laskelmat.,
lyhyesti sanottuna sarjapiirillä määritellään olevan vain yksi polku, jonka läpi virta voi virrata. Tämän määritelmän, kolme säännöt-sarjan piirejä seuraa: kaikki osat jakavat saman nykyinen; resistanssit lisää tasa-suurempi, koko vastus, ja jännite putoaa lisää tasa-suurempi, koko jännite. Kaikki nämä säännöt löytävät juuri määritelmän sarjan piiri. Jos ymmärrät tämän määritelmän täysin, säännöt eivät ole muuta kuin määritelmän alaviitteitä.
ARVOSTELU:
- Komponentit sarjan piiri jakaa saman nykyinen: ITotal = I1 = I2 = . . .,
- sarjan piirin kokonaisvastus on yhtä suuri kuin yksittäisten vastusten summa: RTotal = R1 + R2+. . . Rn
- Yhteensä jännite sarjan piiri on yhtä suuri kuin summa yksittäisten jännite laskee ETotal = E1 + E2 + . . . En
kokeile Ohmin Lakilaskuriamme Tools-osiossamme.
aiheeseen LIITTYVÄT TAULUKOT:
- Sarja DC-Piirien Käytännön Laskentataulukon Vastauksia Laskentataulukon
- Algebrallinen Yhtälö Manipulointi Sähkö-Piirejä Laskentataulukon