Yksi asia, että me voidaan tehdä paljon algoritmeja tässä sarjassa on graph traversal. Mitä tämä tarkoittaa?
Pohjimmiltaan, idea on, että lähdemme liikkeelle noin kuvaajan yhdestä kärki toiseen ja löytää ominaisuuksia niiden suhteita toisiinsa.
Kaksi yleisimmin käytetyt algoritmit, joita käytämme paljon on: Syvyys-Ensimmäinen Haku (DFS) ja Leveys-Ensimmäinen Haku (BFS).,
vaikka molemmat algoritmit mahdollistavat graafien läpiajon, ne eroavat toisistaan eri tavoin. Aloitetaan DFS: stä.
DFS hyödyntää toteutuksessaan ”go deep, head first” – filosofiaa. Ajatuksena on, että alkaen alkuperäinen huippupiste (tai paikka), menemme yhtä polkua, kunnes saavumme loppuun ja jos emme saavu määränpäähän, sitten tulemme takaisin ja mennä eri polkua.
katsotaan esimerkkiä., Oletetaan, että meillä on suunnattu graafi, joka näyttää tältä:

Nyt ajatuksena on, että aloitetaan vertex s ja olemme pyytäneet löytää vertex t. Käyttämällä DFS, aiomme tutkia yksi polku, mennä aina loppuun ja jos emme löydä t, sitten mennään alas toisen polun., Tässä on prosessi:

Joten tässä, me menemme alas polku (p1) ensimmäisen naapurimaiden vertex ja me näemme, että se ei ole loppua, koska se on polku kohti toista vertex., Joten me mennä alas, että tie:
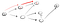
Tämä ei selvästikään ole vertex t joten meidän täytyy mennä takaisin, koska olemme umpikujassa. Koska edellisessä solmussa ei ole enää naapureita, palaamme s: ään., S, me mennä sen toisen naapurimaiden solmu:
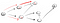
Going alas polkua (p2), olemme joutuneet kolme naapureita., Koska ensimmäinen yksi on jo käynyt, meidän täytyy mennä alas toinen:
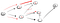
Nyt, jälleen kerran olemme umpikujassa, että ei ole vertex t joten meidän täytyy mennä takaisin., Koska siellä on toinen naapuri, joka ei ole käynyt, me menemme alas, että naapurimaiden polku ja vihdoin löysimme vertex t:

Tämä on miten DFS toimii. Mene polkua pitkin ja jatka, kunnes olet saavuttanut määränpään tai umpikujan. Jos se on määränpää, olet mennyttä. Jos ei, sitten mennä takaisin ja jatkaa alas eri polkua, kunnes olet käyttänyt kaikki vaihtoehdot, että polku.,
– Voimme nähdä, että me noudatamme samaa menettelyä kussakin huippupiste, että meillä käy:
Tehdä DFS kunkin naapuri vertex
Koska tämä edellyttää tekee saman menettelyn kussakin vaiheessa, jotain kertoo meille, että meidän täytyy käyttää rekursio toteuttaa tätä algoritmia.
Tässä on koodi JavaScript:
Huomautus: Tämä erityinen DFS-algoritmi antaa meille mahdollisuuden määrittää, jos se on mahdollista päästä paikasta toiseen., DFS: ää voidaan käyttää monin eri tavoin ja yllä olevaan algoritmiin voi tulla hienovaraisia muutoksia. Yleiskäsite pysyy kuitenkin samana.
Analyysi DFS
Nyt katsotaanpa analysoida tätä algoritmia. Koska olemme liikkumisesta läpi kunkin naapuri solmun ja olemme välittämättä vieraili niistä, meillä on runtime O(V + E).
nopea selitys mitä V+E tarkoittaa:
V edustaa yhteensä pisteiden lukumäärä. E edustaa särmien kokonaismäärää. Jokaisessa huippupisteessä on useita reunoja.,
vaikka voikin tuntua siltä, että joku voi saada uskomaan, että se on V•E V + E: n sijaan, mietitään, mitä V•E tarkalleen tarkoittaa.jotain V•E, se tarkoittaisi, että kunkin huippupiste, meidän täytyy katsoa kaikki reunat kuvaaja riippumatta siitä, onko tai ei ne reunat ovat yhteydessä erityisiä kärki.
Vaikka, toisaalta, V + E tarkoittaa, että kunkin huippupiste, me vain katsoa määrä reunoja, jotka liittyvät että huippupiste. Muista edellisestä viestistä, että tila, jonka otamme adjacency-luetteloon, on O (V + E)., Kunkin huippupiste on useita reunoja ja pahimmassa tapauksessa, jos me suorita DFS kunkin huippupiste, meidän olisi pitänyt tehdä O(V) työskennellä yhdessä, tutkia kaikki reunat vertices, joka on O(E). Kun olemme katsoneet Kaikki V määrä vertices, olisimme myös katsoneet yhteensä e reunat. Siksi, se on V + E.
Nyt, koska DFS käyttää rekursio kunkin huippupiste, joka tarkoittaa sitä, että pino on käytetty (joka on, miksi sitä kutsutaan pinon ylivuoto virhe, kun voit törmätä ääretön rekursiivinen kutsu). Siksi avaruuden monimutkaisuus on O (V).,
nyt katsotaan, miten leveys-ensimmäinen haku eroaa.
Leveys-Ensimmäinen Haku
Leveys-Ensimmäinen Haku (BFS) seuraa ”mennä ohi, bird ’ s eye-view” – filosofiaa. Mitä se tarkoittaa periaatteessa sitä, että sen sijaan menee kaikki alas yhden polun loppuun, BFS liikkuu kohti määränpäätä yksi naapuri kerrallaan., Katsotaanpa, mitä se tarkoittaa:

Joten sen sijaan, että vain menee aina alas sen ensimmäinen naapuri, BFS olisi käydä kaikki naapurit s ensin ja sitten käy näiden naapureiden naapurit ja niin edelleen, kunnes se saavuttaa t.,fd17d”> 

See how different DFS and BFS behave?, Vaikka haluaisin ajatella, että DFS tykkää mennä eteenpäin, BFS haluaa katsoa ottaa sen hitaasti ja tarkkailla kaikkea askel kerrallaan.
nyt yhden meille erottuvan kysymyksen pitäisi olla: ”mistä tiedämme, ketkä naapurit käyvät ensin s: n naapureista?”
– voimme hyödyntää jono on first-in-first-out (FIFO) – ominaisuuden, jossa me pop ensimmäisen huippupiste jonossa, lisää sen avaamaton naapurit jonossa, ja sitten tätä prosessia jatketaan, kunnes jono on joko tyhjä tai vertex lisäämme sen on vertex olemme etsineet.,
Nyt katsotaanpa koodi JavaScript:
Analyysi BFS
Se voi tuntua BFS on hitaampaa. Mutta jos katsot tarkkaan visualisointeja sekä BFS ja DFS, huomaat, että ne itse asiassa ovat saman runtime.
jono varmistaa, että korkeintaan jokainen huippupiste käsitellään, kunnes se saavuttaa määränpään. Joten se tarkoittaa pahimmassa tapauksessa, BFS myös tarkastella kaikkia vertices ja kaikki reunat.,
Kun BFS voi tuntua hitaampi, se on oikeastaan katsotaan nopeammin, koska jos olisimme toteuttamiseksi suurempia kaavioita, huomaat, että DFS jätteiden paljon aikaa menee alas pitkiä polkuja, jotka ovat lopulta väärässä. Itse asiassa, BFS käytetään usein algoritmeja määrittää lyhin polku yhdestä kärki toiseen, mutta me käsitellä niitä myöhemmin.
Niin, koska käyntiajat ovat samat, BFS on runtime O(V + E) ja koska käyttö jono, joka mahtuu korkeintaan V vertices, se on tilavaativuus O(V).,
Analogioita Lähteä Pois
– haluan jättää sinut pois muita tapoja, että olen henkilökohtaisesti kuvitella, miten DFS ja BFS työtä, toivoo, että se auttaa sinua muistamaan yhtä hyvin.
– Aina kun luulen, DFS, haluan ajatella jotain, että löytää oikea polku, jonka törmäämättä paljon umpikujia. Yleensä tämä olisi kuin hiiret, jotka menevät labyrintin läpi etsimään ruokaa.,olisi kokeilla polku löytää ulos, että polku on umpikuja, sitten pivot toisen polun ja toista tämä prosessi, kunnes se saavuttaa tavoitteensa:

Ja tämä on mitä on yksinkertaistettu versio prosessi näyttäisi:

Nyt BFS, Olen aina kuvitellut, että se niin kuin aaltoilu.,div>

aivan kuten miten BFS alkaa lähteestä ja vierailut lähde naapurit ensin ja sitten menee enemmän ulospäin käymällä heidän naapurit ja niin edelleen:

Yhteenveto
- Syvyys-Ensimmäinen Haku (DFS) ja Leveys-Ensimmäinen Haku (BFS) ovat molemmat käytetty kulkea kuvaajia.,
- DFS maksut alas yksi polku, kunnes se on käytetty loppuun, että polku löytää sen kohde, kun BFS torstai kautta naapurimaiden vertices löytää kohteensa.
- DFS käyttää pinoa, kun taas BFS käyttää jonoa.
- sekä DFS: n että BFS: n runtime on O(V + E) ja A space complexity of O(V).
- Molemmat algoritmit on eri filosofioita, mutta yhtä suuri merkitys siinä, miten me kulkea kuvaajia.