Todennäköisyys Jakelu | Tyyppisiä Jakoja

Johdanto

Tervetuloa maailmaan Todennäköisyys Data Science! Aloitan tästä intuitiivisella esimerkillä.

Oletetaan, että olet opettaja yliopistossa. Kun olet tarkistanut tehtäviä viikon, luokittelit kaikki oppilaat. Annoit nämä lajitellut papereita tietojen syöttö kaveri yliopisto ja kertoa hänelle, luoda laskentataulukon, joka sisältää arvosanat kaikista opiskelijoista., Mutta kaveri säilyttää vain arvosanat eikä vastaavia oppilaita.

hän teki toisen kömmähdyksen, häneltä jäi kiireessä pari merkintää väliin, eikä meillä ole aavistustakaan, kenen arvosanat puuttuvat. Etsitään keino ratkaista tämä.

yksi tapa on, että visualisoit arvosanat ja näet, löytyykö datasta trendi.

kuvaaja, että sinulla on tontti kutsutaan taajuus jakelu tiedot. Näet, että on olemassa tasainen käyrä, kuten rakenne, joka määrittelee tietomme,mutta huomaatko poikkeaman?, Meillä on poikkeuksellisen alhainen taajuus tietyllä pistealueella. Paras arvaus olisi siis se, että puuttuvat arvot poistaisivat lommon jakaumassa.

näin yrittäisit ratkaista tosielämän ongelman data-analyysin avulla. Tieteentekijälle, opiskelijalle tai harjoittajalle jakelu on pakollinen tietynlainen käsite. Se tarjoaa perustan analytiikalle ja johdettavalle tilastolle.

vaikka todennäköisyyden käsite antaa meille matemaattiset laskelmat, jakaumat auttavat meitä todella visualisoimaan, mitä alla tapahtuu.,

tässä artikkelissa olen käsitellyt joitakin tärkeitä todennäköisyys jakaumat, jotka on selitetty selkeästi sekä kattavasti.

huomautus: tässä artikkelissa oletetaan, että sinulla on perustietämys todennäköisyydestä. Jos ei, voit viitata tähän todennäköisyysjakaumaan.,

Sisällysluettelo

Yhteiset tietotyypit
erilaisia Jakaumia
1. Bernoulli Jakelu
2. Yhtenäinen Jakelu
3. binomijakauman
4. Normaali Jakelu
5. Poisson Jakelu
6. eksponenttijakauma
Suhteet Jakaumat
Testaa tietosi!

Yleiset tietotyypit

Ennen kuin voimme hypätä selitys jakaumat, katsotaanpa, millaisia tietoja hän voi kohdata. Tiedot voivat olla erillisiä tai jatkuvia.,

diskreetti Data, kuten nimestä voi päätellä, voi ottaa vain määritellyt arvot. Esimerkiksi, kun rullata kuolee, mahdolliset tulokset ovat 1, 2, 3, 4, 5 tai 6 eikä 1,5 tai 2,45.

jatkuva tieto voi ottaa minkä tahansa arvon tietyllä vaihteluvälillä. Levinneisyysalue voi olla äärellinen tai ääretön. Esimerkiksi tytön paino tai pituus, tien pituus. Paino tyttö voi olla mikä tahansa arvo 54 kg, tai 54.5 kg, tai 54.5436 kg.

nyt aloitetaan jakotyypeistä.,

Tyypit Jakaumat

Bernoulli-Jakauman

aloitetaan helpoin jakelu, joka on Bernoulli-Jakauma. Se on itse asiassa helpompi ymmärtää kuin miltä se kuulostaa!

All you cricket junkies Out there! Miten minkä tahansa krikettiottelun alussa päätetään, kuka lyö tai pallottaa? Heitto! Kaikki riippuu siitä, voitatko vai häviätkö heiton. Sanotaan, että jos heitto johtaa päähän, sinä voitat. Muuten häviät. Keskitietä ei ole.

Bernoulli-jakauma on vain kaksi mahdollista lopputulosta, eli 1 (menestys) ja 0 (ei), ja yhden oikeudenkäynnin., Niin satunnaismuuttuja X joka on Bernoulli-jakauma voi ottaa arvon 1 todennäköisyys menestys, sano p, ja arvon 0 todennäköisyydellä vika, sanovat q tai 1-p.

Tässä, esiintyminen pää tarkoittaa menestys, ja esiintyminen hännän tarkoittaa vika.
todennäköisyys saada pää = 0,5 = todennäköisyys saada häntä, koska mahdollisia tuloksia on vain kaksi.

todennäköisyysmassafunktion antaa: px(1-p)1-x missä x € (0, 1).,
Se voi myös olla kirjoitettu

onnistumisen ja epäonnistumisen mahdollisuuksia ei tarvitse olla yhtä todennäköistä, kuin seurausta taistelua ja minun välillä Undertaker. Hän on aika varma voitosta. Joten tässä tapauksessa, todennäköisyys menestys on 0,15 kun minun vika on 0.85

Tässä, onnistumisen todennäköisyys(p) ei ole sama kuin todennäköisyys vika. Alla olevassa kaaviossa näkyy Bernoullin Ottelujakauma.

Tässä, onnistumisen todennäköisyys = 0,15 ja epäonnistumisen todennäköisyys = 0.85., Odotusarvo on juuri sitä miltä se kuulostaa. Jos lyön sinua, saatan odottaa sinun lyövän minua takaisin. Jakauman keskiarvo on periaatteessa minkä tahansa jakauman odotusarvo., Odotusarvo satunnaismuuttujan X a Bernoulli-jakauma on löytynyt seuraavasti:

E(X) = 1*p + 0*(1-p) = p

varianssi satunnaismuuttujan a bernoulli-jakauma on:

V(X) = E(X2) – 2 = p – p2 = p(1-p)

On olemassa monia esimerkkejä, Bernoulli-jakauma, kuten onko se sade huomenna tai ei, missä sade tarkoittaa menestystä ja ei sadetta tarkoittaa epäonnistumista ja Voittaa (menestys) tai menettää (vika) peli.

tasainen Jakautuminen

Kun heität oikeudenmukainen kuolla, tulokset ovat 1-6., Todennäköisyydet saada nämä tulokset ovat yhtä todennäköisiä, ja että on perusta tasaisen. Bernoullin jakaumasta poiketen kaikki yhtenäisen jakauman mahdollisten tulosten n lukumäärä on yhtä todennäköinen.

muuttujan X sanotaan olevan tasaisesti jakautunut, jos sen tiheysfunktio on:

kuvaaja tasaisen käyrä näyttää

Voit nähdä, että muoto tasaisen käyrä on suorakulmainen, syy, miksi tasaisen kutsutaan suorakulmainen jakelu.,

Tasajakaumassa A ja b ovat parametrit.

kukkakaupassa päivittäin myytävien kukkakimppujen määrä jakautuu tasaisesti maksimissaan 40 ja minimissään 10.

kokeillaan laskea todennäköisyys, että päivittäinen myynti laskee 15-30: n välillä.

todennäköisyys, että päivittäinen myynti laskee välillä 15 ja 30 on (30-15)*(1/(40-10)) = 0.5

Vastaavasti todennäköisyys, että päivittäinen myynti on suurempi kuin 20 on = 0.,667

keskiarvo ja varianssi X seuraavat yhtenäinen jakelu on:

Keskiarvo -> E(X) = (a+b)/2

Varianssi -> V(X) = (b-a)2/12

standardi yhtenäinen tiheys on parametreilla a = 0 ja b = 1, niin PDF-standardi yhtenäinen tiheys saadaan kaavasta:

binomijakauman

palataanpa kriketti. Oletetaan, että voitit heiton tänään ja tämä osoittaa onnistuneen tapahtuman. Heität taas, mutta hävisit tällä kertaa., Jos voitat heiton tänään, tämä ei edellytä, että voitat heiton huomenna. Annetaan satunnaismuuttuja, sanotaan X, – kuinka monta kertaa voitit heiton. Mikä voi olla X: n mahdollinen arvo? Se voi olla mikä tahansa numero riippuen siitä, kuinka monta kertaa heitit kolikon.

mahdollisia tuloksia on vain kaksi. Pää osoittaa menestystä ja häntä osoittaa epäonnistuminen. Näin ollen, todennäköisyys saada pää = 0.5 ja epäonnistumisen todennäköisyys voidaan helposti laskea seuraavasti: q = 1 – p = 0.5.,

jakelu, jossa vain kaksi tulokset ovat mahdollisia, kuten onnistuminen tai epäonnistuminen, voitto tai tappio, voittaa tai menettää ja missä todennäköisyys menestyminen ja epäonnistuminen on sama kaikissa tutkimuksissa kutsutaan binomijakauman.

tulosten ei tarvitse olla yhtä todennäköisiä. Muistatko esimerkin tappelusta minun ja Undertakerin välillä? Joten, jos todennäköisyys onnistua kokeessa on 0,2 niin epäonnistumisen todennäköisyys voidaan helposti laskea q = 1-0,2 = 0,8.

jokainen kokeilu on itsenäinen, sillä edellisen heiton tulos ei määritä tai vaikuta nykyisen heiton lopputulokseen., Kokeilu, jossa on vain kaksi mahdollista lopputulosta toistetaan n monta kertaa on nimeltään binomisen. Binomijakauman parametrit ovat n ja p, jossa n on kokeiden kokonaismäärä ja p on onnistumisen todennäköisyys kussakin kokeessa.

perusteella edellä selitys, ominaisuuksia binomijakauman ovat

Jokainen oikeudenkäynti on riippumaton.
kokeessa on vain kaksi mahdollista lopputulosta-joko onnistuminen tai epäonnistuminen.
n identtisiä kokeita tehdään yhteensä useita.
onnistumisen ja epäonnistumisen todennäköisyys on sama kaikissa tutkimuksissa., (Kokeet ovat identtisiä.,

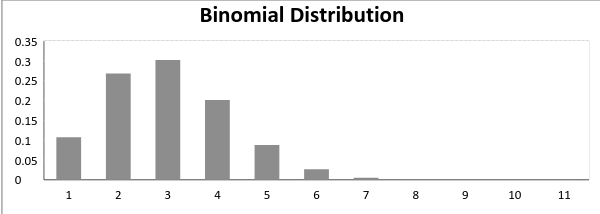
Nyt, kun onnistumisen todennäköisyys = epäonnistumisen todennäköisyys tällaisessa tilanteessa kuvaaja binomijakauman näyttää siltä,

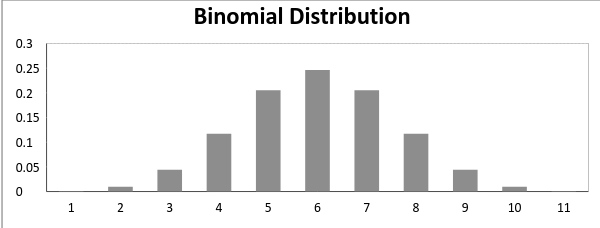
keskiarvo ja varianssi binomijakauman annetaan:

Keskiarvo -> µ = n*p

Varianssi -> Var(X) = n*p*q,

Normaali Jakelu

normaalijakauma edustaa käyttäytymistä useimmissa tilanteissa maailmankaikkeudessa (Joka on, miksi sitä kutsutaan ”normaali” jakelu., Niin kai.). (Pienten) satunnaismuuttujien suuri summa osoittautuu usein tavanomaisesti hajautetuksi, mikä edistää sen laajaa soveltamista. Kaikki jakelu on tunnettu normaalijakauman jos se on seuraavat ominaisuudet:
1. keskiarvo, mediaani ja moodi jakelu samaan aikaan.
2. jakauman käyrä on kellomainen ja symmetrinen viivan x=μ suhteen.
3. kokonaispinta-ala käyrän alla on 1.
4. tasan puolet arvoista on keskustan vasemmalla puolella ja toinen puoli oikealla.,
normaalijakauma poikkeaa suuresti Binomijakaumasta. Kuitenkin, jos kokeilujen määrä lähestyy ääretöntä niin muodot ovat melko samanlaisia.

PDF satunnaismuuttuja X seuraavasti normaali jakelu on annettu:

keskiarvo ja varianssi satunnaismuuttujan X, joka on sanottu olevan normaalisti jakautunut saadaan:

Keskiarvo -> E(X) = µ

Varianssi -> Var(X) = σ^2,

Tässä, µ (keskiarvo) ja σ (keskihajonta) ovat parametreja.,
alla on esitetty satunnaismuuttujan X ~ n (µ, σ) kuvaaja.

standardi normaalijakauma on määritelty jakauma, jonka keskiarvo on 0 ja keskihajonta 1. Tällaisessa tapauksessa PDF-tiedosto tulee:

Poisson-Jakauma

Oletetaan, että olet töissä call center, noin kuinka monta puhelua saat päivässä? Se voi olla mikä tahansa numero. Nyt puhelinpalvelun koko puhelumäärä päivässä mallinnetaan Poisson-jakelulla., Muita esimerkkejä ovat
1. sairaalassa päivässä kirjattujen hätäpuhelujen määrä.
2. alueella vuorokauden aikana ilmoitettujen varkauksien määrä.
3. salonkiin tunnissa saapuvien asiakkaiden määrä.
4. tietyssä kaupungissa raportoitujen itsemurhien määrä.
5. painovirheiden määrä kirjan jokaisella sivulla.
voit nyt ajatella monia esimerkkejä saman kurssin jälkeen., Poisson-Jakauma on sovellettavissa tilanteissa, joissa tapahtumat tapahtuvat sattumanvaraisesti pistettä ajan ja avaruuden, jossa meidän etu on vain määrä esiintymiä tapahtuma.

jakelu kutsutaan Poisson-jakaumaa, kun seuraavat oletukset ovat voimassa:

1. Mikä tahansa onnistunut tapahtuma ei saisi vaikuttaa toisen onnistuneen tapahtuman lopputulokseen.
2. Onnistumisen todennäköisyyden lyhyellä aikavälillä on vastattava onnistumisen todennäköisyyttä pidemmällä aikavälillä.
3. Onnistumisen todennäköisyys intervallissa lähestyy nollaa, kun intervalli pienenee.,

nyt, jos jokin jakauma validoi edellä mainitut oletukset, se on Poissonin jakauma. Joitakin merkintöjä käytetään Poisson-jakauma on:
- λ on nopeus, jolla tapahtuma tapahtuu,
- t on pitkä aikaväli,
- Ja X on joukko tapahtumia, jotka aikaväli.
Tässä, X kutsutaan Poisson-satunnaismuuttuja ja todennäköisyysjakauma X kutsutaan Poisson-jakauma.

Let µ kuvaamaan tapahtumien keskiarvoa pituusvälillä t. sitten µ = λ*t.,

PMF X seuraavat Poisson-jakauma saadaan kaavasta:

keskiarvo µ on parametrin tämä jakelu. µ määritellään myös tämän intervallin λ-kertaiseksi pituudeksi. Kuvaaja Poisson-jakauma on esitetty alla:

alla Oleva kaavio havainnollistaa muutos käyrä, koska kasvu tarkoittaa.

– Se on havaittavissa, että keskimääräinen nousu, käyrä siirtyy oikealle.,

keskiarvo ja varianssi X seuraavat Poisson-jakauma:

Keskiarvo -> E(X) = µ
Varianssi -> Var(X) = µ

eksponenttijakauma

tarkastellaan call center-esimerkiksi yksi enemmän aikaa. Entä soittojen välinen aika ? Täällä eksponentiaalinen jakauma tulee pelastamaan meidät. Eksponenttijakaumamalleilla soitinten välinen aika.

Muita esimerkkejä ovat:

1. Beteen metro arrivals,
2., Saapumisaikojen pituus huoltoasemalla
3. Ilmastointilaitteen

eksponentiaalisen jakauman käyttöikää käytetään laajalti selviytymisanalyysissä. Koneen odotetusta elämästä ihmisen odotettuun elämään eksponentiaalinen jakautuminen tuottaa tuloksen onnistuneesti.

satunnaismuuttujan X sanotaan olevan eksponentiaalista jakaumaa PDF:

f(x) = { λe-λx, x ≥ 0,

ja parametri λ>0, joka on myös nimeltään korko.,

selviytyminen analyysi, λ on nimeltään kuolleisuus laitteen milloin tahansa t, kun otetaan huomioon, että se on kestänyt ajan t.

Keskiarvo ja Varianssi satunnaismuuttujan X seuraavat eksponentiaalinen jakelu:

Keskiarvo -> E(X) = 1/λ

Varianssi -> Var(X) = (1/λ)2

Myös, suurempi korko on, sitä nopeammin käyrä laskee ja pienempi korko, tasaisempi käyrä. Tämä selitetään paremmin alla olevalla graafilla.,

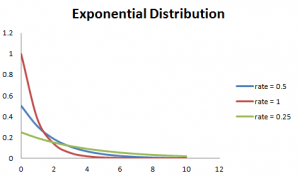
helpottaa laskentaa, on olemassa joitakin kaavoja alla.
P{X≤x} = 1 – e-λx, vastaa ala tiheys käyrä vasemmalle x.

P{X>x} = e-λx, vastaa ala tiheys käyrä oikealle x.

P{x1<X≤ x2} = e-λx1 – e-λx2, vastaa ala tiheys käyrä, väli x1 ja x2.

Suhteiden Jakaumat

Suhde Bernoulli ja binomijakauman

1., Bernoullin jakelu on binomijakauman erikoistapaus yhdellä oikeudenkäynnillä.

2. Bernoullin ja binomijakauman mahdollisia tuloksia on vain kaksi eli menestys ja epäonnistuminen.

3. Sekä Bernoullilla että Binomijakaumilla on itsenäiset polut.

Suhde Poissonin jakauman ja binomijakauman

Poisson Jakelu on rajoittava tapauksessa binomijakauma seuraavin edellytyksin:
1. tutkimusten määrä on toistaiseksi suuri tai n → ∞.,
2. onnistumisen todennäköisyys jokaiselle kokeilulle on sama ja loputtomasti pieni tai P →0.
3. NP = λ, on äärellinen.
välisen Suhteen Normaali-ja binomijakauman & Normaali-ja Poisson-Jakauma:

Normaali jakelu on toinen rajoittava muoto binomijakauman seuraavin edellytyksin:
1. tutkimusten määrä on toistaiseksi suuri, n → ∞.
2. sekä p että q eivät ole loputtomiin pieniä.
normaalijakauma on myös Poisson-jakauman rajoittava tapaus parametrilla λ →∞.,

välisen Suhteen Eksponentti-ja Poisson-Jakauma:

Jos ajat välillä satunnaisia tapahtumia noudattaa eksponentiaalista jakaumaa korko λ, niin kokonaismäärä tapahtumia ajanjakson pituus t noudattaa Poisson-jakaumaa parametrilla λt.

Testaa tietosi

Olet tullut näin pitkälle. Osaatko vastata seuraaviin kysymyksiin? Kerro alla olevissa kommenteissa!

1. Kaava laskea standardoidun normaalijakauman satunnaismuuttujan on:

a. (x+µ) / σ
b. (x-µ) / σ
c. (x-σ) / µ

2., Vuonna Bernoulli-Jakauma, laskentakaava keskihajonta saadaan kaavalla:

a. p (1 – p)
b. SQRT(s(s – 1))
c. SQRT(p(1 – p))

3. Normaali jakelu, kasvua siis on:

a. vaihto-käyrä vasemmalle
b. siirtää käyrää oikealle
c. tasoita käyrä

4. Akun käyttöikä jakautuu eksponentiaalisesti λ = 0,05 tunnissa. Todennäköisyys sille, että akku kestää 10-15 tuntia, on:

a.0.1341
b.0.1540
c.0.,0079

End Huomautuksia

Todennäköisyys Jakaumat ovat yleisiä monilla aloilla, nimittäin -, vakuutus -, fysiikan, tekniikan, tietotekniikan ja jopa sosiaalinen tiede, jossa opiskelijat psykologian ja lääketieteen ovat laajasti käyttäen todennäköisyys jakaumat. Se on helppo sovellus, ja laaja käyttö. Tässä kirjoituksessa tuotiin esiin kuusi tärkeää jakoa, jotka havaitaan jokapäiväisessä elämässä, ja selitettiin niiden soveltamista. Nyt voit tunnistaa, suhteuttaa ja erottaa nämä jakaumat.,

Jos sinulla on epäilyksiä ja haluat nähdä lisää artikkeleita jakeluista, kirjoita alla olevaan kommenttiosioon. Syvempää kirjoittaa näistä jakaumista, voit viitata tähän resurssiin.