en esta página, describiremos los tres principios que debe entender con respecto a los circuitos en serie:
- corriente: la cantidad de corriente es la misma a través de cualquier componente en un circuito en serie.
- Resistencia: la resistencia total de cualquier circuito en serie es igual a la suma de las resistencias individuales.
- tensión: la tensión de alimentación en un circuito en serie es igual a la suma de las caídas de tensión individuales.,
echemos un vistazo a algunos ejemplos de circuitos en serie que demuestran estos principios.
comenzaremos con un circuito en serie que consta de tres resistencias y una sola batería:

el primer principio para entender acerca de los circuitos en serie es el siguiente:
la cantidad de corriente en un circuito en serie es la misma a través de cualquier componente en el circuito.
esto se debe a que solo hay una ruta para el flujo de corriente en un circuito en serie., Debido a que la carga eléctrica fluye a través de conductores como canicas en un tubo, la velocidad de flujo (velocidad de canica) en cualquier punto del circuito (tubo) en cualquier punto específico en el tiempo debe ser igual.
usando la Ley de Ohm en circuitos en serie
de la forma en que está dispuesta la batería de 9 voltios, podemos decir que la corriente en este circuito fluirá en el sentido de las agujas del reloj, del punto 1 al 2 al 3 al 4 y de vuelta a 1. Sin embargo, tenemos una fuente de voltaje y tres resistencias. ¿Cómo usamos la Ley de Ohm aquí?,
una advertencia importante a la Ley de Ohm es que todas las cantidades (voltaje, corriente, resistencia y potencia) deben relacionarse entre sí en términos de los mismos dos puntos en un circuito. Podemos ver este concepto en acción en el ejemplo de circuito de resistencia simple a continuación.,
usando la Ley de Ohm en un circuito de resistencia simple y simple
con un circuito de resistencia simple de una sola batería, podríamos calcular fácilmente cualquier cantidad porque todos se aplicaron a los mismos dos puntos en el circuito:


dado que los puntos 1 y 2 están conectados junto con el cable de resistencia insignificante, al igual que los puntos 3 y 4, podemos decir que el punto 1 es eléctricamente común al punto 2, y que el punto 3 es eléctricamente común al punto 4., Como sabemos que tenemos 9 voltios de fuerza electromotriz entre los puntos 1 y 4 (directamente a través de la batería), y como el punto 2 es común al punto 1 y el punto 3 común al punto 4, también debemos tener 9 voltios entre los puntos 2 y 3 (directamente a través de la resistencia).
Por lo tanto, podemos aplicar la Ley de Ohm (I = E/R) a la corriente a través de la resistencia, porque conocemos el voltaje (E) a través de la resistencia y la resistencia (R) de esa resistencia. Todos los Términos (E, I, R) se aplican a los mismos dos puntos en el circuito, a esa misma resistencia, por lo que podemos usar la fórmula de la Ley de Ohm sin reservas.,
usando la Ley de Ohm en circuitos con múltiples resistencias
en circuitos que contienen más de una resistencia, debemos tener cuidado en cómo aplicamos la Ley de Ohm. En el circuito de ejemplo de tres resistencias a continuación, sabemos que tenemos 9 voltios entre los puntos 1 y 4, que es la cantidad de fuerza electromotriz que impulsa la corriente a través de la combinación en serie de R1, R2 y R3. Sin embargo, no podemos tomar el valor de 9 voltios y dividirlo por 3k, 10k o 5k Ω para tratar de encontrar un valor de corriente, porque no sabemos cuánto voltaje hay a través de cualquiera de esas resistencias, individualmente.,

la cifra de 9 voltios es una cantidad total para todo el circuito, mientras que las cifras de 3k, 10k y 5k Ω son cantidades individuales para resistencias individuales. Si tuviéramos que conectar una figura para el voltaje total en la ecuación de la Ley de un Ohm con una figura para la resistencia individual, el resultado no se relacionaría con precisión con ninguna cantidad en el circuito real.,
para R1, la Ley de Ohm relacionará la cantidad de voltaje a través de R1 con la corriente a través de R1, dada la resistencia de R1, 3kΩ:

pero, como no conocemos el voltaje a través de R1 (solo el voltaje total suministrado por la batería a través de la combinación de la serie de tres resistencias) y no conocemos la corriente a través de R1, no podemos hacer ningún cálculo con cualquiera de las fórmulas. Lo mismo ocurre con R2 y R3: podemos aplicar las ecuaciones de la Ley de Ohm si y solo si todos los términos son representativos de sus respectivas cantidades entre los mismos dos puntos en el circuito.,
Entonces, ¿qué podemos hacer? Sabemos el voltaje de la fuente (9 voltios) aplicado a través de la combinación de serie de R1, R2 y R3, y sabemos la resistencia de cada resistencia, pero como esas cantidades no están en el mismo contexto, no podemos usar la Ley de Ohm para determinar la corriente del circuito. Si solo supiéramos Cuál es la resistencia total para el circuito: entonces podríamos calcular la corriente total con nuestra cifra para el voltaje total (I=E/R).,
combinando múltiples resistencias en una resistencia total equivalente
esto nos lleva al segundo principio de los circuitos en serie:
la resistencia total de cualquier circuito en serie es igual a la suma de las resistencias individuales.
esto debería tener sentido intuitivo: cuantas más resistencias en serie tenga que pasar la corriente, más difícil será que fluya la corriente.,
en el problema de ejemplo, teníamos resistencias de 3 kΩ, 10 kΩ y 5 kω en serie, lo que nos da una resistencia total de 18 kΩ:

En esencia, hemos calculado la resistencia equivalente de R1, R2 y R3 combinados.,oltages usando la Ley de Ohm
sabiendo que la corriente es igual a través de todos los componentes de un circuito en serie (y acabamos de determinar la corriente a través de la batería), podemos volver a nuestro esquema de circuito original y anotar la corriente a través de cada componente:
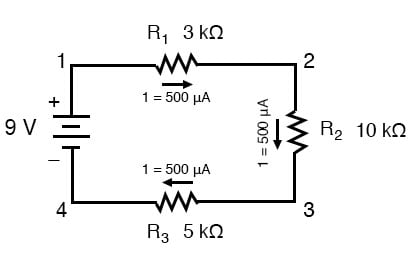
ahora que sabemos la cantidad de corriente a través de cada resistencia, podemos usar la Ley de Ohm para determinar la caída de tensión a través de Ley de Ohm en su contexto apropiado):

observe las caídas de voltaje a través de cada resistencia, y cómo la suma de las caídas de voltaje (1.,5 + 5 + 2.5) es igual a la tensión de la batería (alimentación): 9 voltios.
Este es el tercer principio de los circuitos en serie:
la tensión de alimentación en un circuito en serie es igual a la suma de las caídas de tensión individuales.
analizar circuitos de serie simples con el» método de tabla » y la Ley de Ohm
Sin embargo, el método que acabamos de usar para analizar este circuito de serie simple puede simplificarse para una mejor comprensión., Al usar una tabla para listar todos los voltajes, corrientes y resistencias en el circuito, se hace muy fácil ver cuáles de esas cantidades se pueden relacionar correctamente en cualquier ecuación de Ley de Ohm:

La regla con tal tabla es aplicar la Ley de Ohm solo a los valores dentro de cada columna vertical. Por ejemplo, ER1 solo con IR1 y R1; ER2 solo con IR2 y R2; etc., Comienza su análisis rellenando los elementos de la tabla que se le dan desde el principio:

como puede ver en la disposición de los datos, no podemos aplicar los 9 voltios de ET (voltaje total) a ninguna de las resistencias (R1, R2 o R3) en la fórmula de Ley de cualquier Ohm porque están en columnas diferentes. Los 9 voltios de voltaje de la batería no se aplican directamente a través de R1, R2 o R3. Sin embargo, podemos usar nuestras «reglas» de circuitos en serie para rellenar espacios en blanco en una fila horizontal.,t de 500 µA:

entonces, sabiendo que la corriente es compartida por igual por todos los componentes de un circuito en serie (otra «regla» de circuitos en serie), podemos completar las corrientes para cada resistencia a partir de la figura actual calculada:

finalmente, puede usar la ley de Ohm para determinar la caída de voltaje a través de cada resistencia, una columna a la vez:

verificando cálculos con análisis por computadora (Spice)
solo por diversión, podemos usar una computadora para analizar este mismo circuito automáticamente., Será una buena manera de verificar nuestros cálculos y también familiarizarse con el análisis informático. En primer lugar, tenemos que describir el circuito a la computadora en un formato reconocible por el software.
el programa SPICE que usaremos requiere que todos los puntos eléctricamente únicos en un circuito estén numerados, y la colocación de componentes se entiende por cuál de esos puntos numerados, o «nodos», comparten. Para mayor claridad, numeré las cuatro esquinas de nuestro circuito de ejemplo del 1 al 4., SPICE, sin embargo, exige que haya un nodo cero en algún lugar del circuito, así que redibujaré el circuito, cambiando ligeramente el esquema de numeración:

todo lo que he hecho aquí es volver a numerar la esquina inferior izquierda del circuito 0 en lugar de 4. Ahora, puedo ingresar varias líneas de texto en un archivo de computadora que describe el circuito en términos que SPICE entenderá, completo con un par de líneas adicionales de código que dirigen al programa para mostrar datos de voltaje y corriente para nuestro placer visual., Este archivo de computadora se conoce como netlist en la terminología de SPICE:
series circuit v1 1 0 r1 1 2 3k r2 2 3 10k r3 3 0 5k .dc v1 9 9 1 .print dc v(1,2) v(2,3) v(3,0) .end
ahora, todo lo que tengo que hacer es ejecutar el programa SPICE para procesar la netlist y generar los resultados:
| v1 | V(1,2) | v(2,3) | V(3) | i(V1) |
|---|---|---|---|---|
| 9.000 e+00 | 1.500 e+00 | 5.000 e+00 | 2.500 e+00 | -5.,000E-04 |
Esta impresión nos dice que el voltaje de la batería es de 9 voltios, y las caídas de voltaje a través de R1, R2 y R3 son de 1.5 voltios, 5 voltios y 2.5 voltios, respectivamente. Las caídas de voltaje a través de cualquier componente en SPICE son referenciadas por los números de nodo entre los que se encuentra el componente, por lo que v(1,2) hace referencia al voltaje entre los nodos 1 y 2 en el circuito, que son los puntos entre los que se encuentra R1.,
el orden de los números de nodo es importante: cuando SPICE emite una figura para v (1,2), considera la polaridad de la misma manera que si tuviéramos un voltímetro con el cable de prueba rojo en el nodo 1 y el cable de prueba negro en el nodo 2. También tenemos una pantalla que muestra la corriente (aunque con un valor negativo) a 0.5 miliamperios o 500 microamperios. Así que nuestro análisis matemático ha sido vindicado por la computadora. Esta cifra aparece como un número negativo en el análisis de SPICE, debido a una peculiaridad en la forma en que SPICE maneja los cálculos actuales.,
En resumen, un circuito en serie se define como tener solo un camino a través del cual la corriente puede fluir. A partir de esta definición, se siguen tres reglas de circuitos en serie: todos los componentes comparten la misma corriente; las resistencias se suman a una resistencia total más grande; y las caídas de voltaje se suman a una tensión total más grande. Todas estas reglas encuentran la raíz en la definición de un circuito en serie. Si entiende esa definición completamente, entonces las reglas no son más que notas al pie de la definición.
revisión:
- Los componentes de un circuito en serie comparten la misma corriente: ITotal = I1 = I2=. . ., En
- La resistencia total en un circuito en serie es igual a la suma de las resistencias individuales: RTotal = R1 + R2 + . . . Rn
- La tensión Total en un circuito en serie es igual a la suma de las caídas de tensión individuales ETotal = E1 + E2 + . . . En
pruebe nuestra calculadora de leyes de Ohm en nuestra sección de herramientas.
hojas de Trabajo relacionadas:
- serie DC Circuits práctica Hoja de trabajo con respuestas hoja de trabajo
- manipulación de ecuaciones algebraicas para circuitos eléctricos Hoja de trabajo