una cosa que haremos mucho con los Algoritmos de esta serie es el recorrido de gráficos. ¿Qué significa esto exactamente?
básicamente, la idea es que nos moveremos alrededor del gráfico de un vértice a otro y descubriremos las propiedades de sus relaciones interconectadas.
dos de los algoritmos más utilizados que usaremos mucho son: Búsqueda en profundidad (DFS) y búsqueda en amplitud (BFS).,
si bien ambos algoritmos nos permiten recorrer gráficos, difieren de diversas maneras. Empecemos con DFS.
DFS utiliza la filosofía «go deep, head first» en su implementación. La idea es que a partir de un vértice inicial (o lugar), vamos por un camino hasta llegar al final y si no llegamos a nuestro destino, entonces regresamos y vamos por un camino diferente.
veamos un ejemplo., Supongamos que tenemos un grafo dirigido que se parece a esto:

Ahora, la idea es que empecemos en el vértice s y se nos pide encontrar el vértice t. El uso de DFS, vamos a explorar un camino, ir todo el camino hasta el final y si no encontramos t, luego vamos por otro camino., He aquí el proceso:

Así que aquí vamos por el camino (p1) de la primera vecinos vértice y vemos que no es el final porque tiene una ruta de acceso hacia el otro vértice., Así que ir por ese camino:
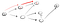
Claramente, este no es el vértice de t así que tenemos que ir hacia atrás, porque hemos llegado a un callejón sin salida. Dado que el nodo anterior no tiene más vecinos, volvemos a S., De s, tenemos que ir a su segunda vecinos de un nodo:
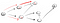
Yendo por el camino (p2), nos enfrentamos con tres vecinos., Desde que el primero ya ha sido visitado, tenemos que ir por el segundo:
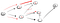
Ahora, una vez más, hemos llegado a un callejón sin salida que no es el vértice de t, de modo que vamos a volver., Ya que no hay otro vecino que no ha sido visitado, vamos que los vecinos del camino y por fin hemos encontrado el vértice t:

Esta es la forma en DFS funciona. Ir por un camino y seguir hasta que haya llegado al destino o un callejón sin salida. Si es el destino, estás acabado. Si no lo es, entonces regresa y continúa por un camino diferente hasta que hayas agotado todas las opciones dentro de ese camino.,
podemos ver que seguimos el mismo procedimiento en cada vértice que visitamos:
hacer un DFS para cada vecino del vértice
dado que esto implica hacer el mismo procedimiento en cada paso, algo nos dice que necesitaremos usar recursión para implementar este algoritmo.
este es el código en JavaScript:
Nota: Este algoritmo DFS nos permite determinar si es posible llegar de un lugar a otro., DFS se puede utilizar de varias maneras y puede haber cambios sutiles en el algoritmo anterior. Sin embargo, el concepto general sigue siendo el mismo.
análisis de DFS
ahora analicemos este algoritmo. Dado que estamos atravesando a través de cada vecino del nodo y estamos ignorando los visitados, tenemos un tiempo de ejecución de O(V + E).
una explicación rápida de exactamente lo que significa V + E:
v representa el número total de vértices. E representa el número total de aristas. Cada vértice tiene un número de aristas., mientras que puede parecer que uno puede ser llevado a creer que es V * E en lugar de V + E, vamos a pensar en lo que V•E significa exactamente.
para que algo sea V * E, significaría que para cada vértice, tenemos que mirar todas las aristas en el gráfico independientemente de si esas aristas están conectadas a ese vértice específico.
mientras que, por otro lado, V + E significa que para cada vértice, solo miramos el número de aristas que pertenecen a ese vértice. Recordemos del post anterior, que el espacio que ocupamos para la lista de adyacencia es O (V + E)., Cada vértice tiene un número de aristas y en el peor de los casos, si tuviéramos que ejecutar DFS en cada vértice, habríamos hecho O(V) trabajo junto con la exploración de todas las aristas de los vértices, que es O(E). Una vez que hemos mirado Todos V Número de vértices, también habríamos mirado un total de E aristas. Por lo tanto, es V + E.
ahora, dado que DFS usa recursión en cada vértice, eso significa que se usa una pila (por lo que se llama un error de desbordamiento de pila cada vez que se encuentra con una llamada recursiva infinita). Por lo tanto, la complejidad del espacio es O(V).,
Ahora vamos a ver en qué difiere la búsqueda PRIMERO en amplitud.
la búsqueda PRIMERO en anchura
la búsqueda PRIMERO en anchura (BFS) sigue la filosofía de «ve de par en par, a vista de pájaro». Lo que básicamente significa es que en lugar de ir todo el camino por un camino hasta el final, BFS se mueve hacia su destino un vecino a la vez., Veamos lo que eso significa:

así que en lugar de ir todo el camino por su primer vecino, BFS visitaría a todos los vecinos de s primero y luego visitaría a los vecinos de esos vecinos y así sucesivamente hasta que alcance t.,fd17d»>


See how different DFS and BFS behave?, Si bien me gusta pensar que a DFS le gusta ir de frente, a BFS le gusta mirar, tomarlo con calma y observar todo paso a paso.
ahora una pregunta que se destaca para nosotros debe ser: «¿Cómo sabemos qué vecinos visitar primero de los vecinos de s?»
bien, podríamos utilizar la propiedad first-in-first-out (FIFO) de una cola donde hacemos estallar el primer vértice de la cola, agregamos sus vecinos no visitados a la cola, y luego continuamos este proceso hasta que la cola esté vacía o el vértice que agregamos a ella es el vértice que hemos estado buscando.,
Ahora veamos el código en JavaScript:
Análisis de BFS
puede parecer BFS es más lento. Pero si observa cuidadosamente las visualizaciones DE BFS y DFS, encontrará que en realidad tienen el mismo tiempo de ejecución.
la cola asegura que a lo sumo cada vértice será procesado hasta que llegue al destino. Eso significa que en el peor de los casos, BFS también mirará todos los vértices y todas las aristas.,
mientras que BFS puede parecer más lento, en realidad se considera más rápido porque si los implementáramos en gráficos más grandes, encontrará que DFS pierde mucho tiempo yendo por caminos largos que en última instancia son incorrectos. De hecho, BFS se usa a menudo en algoritmos para determinar el camino más corto de un vértice a otro, pero los tocaremos más adelante.
así que dado que los tiempos de ejecución son los mismos, BFS tiene un tiempo de ejecución de O (V + E) y debido al uso de una cola que puede contener como máximo V vértices, tiene una complejidad de espacio de O(V).,
analogías para dejarlo con
quiero dejarlo con otras formas que personalmente imagino cómo funcionan DFS y BFS con la esperanza de que le ayude a recordar también.
siempre que pienso en DFS, me gusta pensar en algo que encuentre el camino correcto al toparme con muchos callejones sin salida. Por lo general, esto sería como un ratón que va a través de un laberinto para buscar comida.,se trate de una ruta, saber que el camino es un callejón sin salida, a continuación, gire a otro camino y repita este proceso hasta que llega a su destino:

Y esto es lo que una versión simplificada del proceso sería así:

Ahora, para BFS, Siempre me he imaginado como una onda.,div>

de manera parecida a como BFS se inicia en la fuente y las visitas de la fuente de los vecinos del primero y, a continuación, va más hacia el exterior visitando a sus vecinos, y así sucesivamente:

Resumen
- Búsqueda en Profundidad (DFS) y la Búsqueda en Anchura (BFS) son utilizados para recorrer los gráficos.,
- DFS carga por un camino hasta que ha agotado ese camino para encontrar su objetivo, mientras que BFS ondula a través de los vértices vecinos para encontrar su objetivo.
- DFS usa una pila mientras que BFS usa una cola.
- tanto DFS como BFS tienen un tiempo de ejecución de O (V + E) y una complejidad de espacio de O(V).
- ambos algoritmos tienen filosofías diferentes pero comparten la misma importancia en la forma en que atravesamos los gráficos.