Introducción
¡Bienvenido al mundo de la probabilidad en la ciencia de datos! Permítanme comenzar las cosas con un ejemplo intuitivo.
supongamos que usted es profesor en una universidad. Después de revisar las tareas durante una semana, calificó a todos los estudiantes. Le diste estos trabajos calificados a un tipo de entrada de datos en la universidad y le dijiste que creara una hoja de cálculo que contuviera las calificaciones de todos los estudiantes., Pero el tipo solo almacena las calificaciones y no los estudiantes correspondientes.

cometió otro error, se perdió un par de entradas a toda prisa y no tenemos idea de qué calificaciones faltan. Vamos a encontrar una manera de resolver esto.
una forma es que visualice las calificaciones y vea si puede encontrar una tendencia en los datos.

El gráfico que tiene la parcela se denomina distribución de frecuencias de los datos. Ves que hay una curva suave como la estructura que define nuestros datos, pero ¿notas una anomalía?, Tenemos una frecuencia anormalmente baja en un rango de puntuación particular. Así que la mejor suposición sería tener valores faltantes que eliminan la abolladura en la distribución.
así es como tratarías de resolver un problema de la vida real usando el análisis de datos. Para cualquier científico de datos, un estudiante o un profesional, la distribución es un concepto que debe conocer. Proporciona la base para el análisis y las estadísticas inferenciales.
mientras que el concepto de probabilidad nos da los cálculos matemáticos, las distribuciones nos ayudan a visualizar realmente lo que está sucediendo debajo.,
en este artículo, he cubierto algunas distribuciones de probabilidad importantes que se explican de manera lúcida y exhaustiva.
Nota: Este artículo asume que usted tiene un conocimiento básico de probabilidad. Si no, puede referirse a estas distribuciones de probabilidad.,
Tabla de Contenido
- Común de Tipos de Datos
- Tipos de Distribuciones
- Bernoulli Distribución
- Distribución Uniforme
- Distribución Binomial
- Distribución Normal
- Distribución de Poisson
- Distribución Exponencial
- las Relaciones entre las Distribuciones
- pon a Prueba tus Conocimientos!
tipos de datos comunes
antes de pasar a la explicación de las distribuciones, veamos qué tipo de datos podemos encontrar. Los datos pueden ser discretos o continuos.,
Los datos discretos, como su nombre indica, solo pueden tomar valores especificados. Por ejemplo, cuando haces rodar un dado, los resultados posibles son 1, 2, 3, 4, 5 o 6 y no 1.5 o 2.45.
Los datos continuos pueden tomar cualquier valor dentro de un rango dado. El rango puede ser finito o infinito. Por ejemplo, el peso o la altura de una niña, la longitud de la carretera. El peso de una niña puede ser cualquier valor de 54 kgs, o 54.5 kgs, o 54.5436 kgs.
ahora comencemos con los tipos de distribuciones.,
tipos de Distribuciones
distribución Bernoulli
comencemos con la distribución más fácil que es la distribución Bernoulli. En realidad, es más fácil de entender de lo que parece!
todos ustedes adictos al cricket por ahí! Al comienzo de cualquier partido de cricket, ¿cómo se decide quién va a batear o pelota? ¡Un lanzamiento! Todo depende de si ganas o pierdes el lanzamiento, ¿verdad? Digamos que si el lanzamiento resulta en una cabeza, Usted gana. Si no, pierdes. No hay midway.
una distribución de Bernoulli solo tiene dos resultados posibles, a saber, 1 (éxito) y 0 (fracaso), y un solo ensayo., Así que la variable aleatoria X que tiene una distribución de Bernoulli puede tomar el valor 1 con la probabilidad de éxito, digamos p, y el valor 0 con la probabilidad de fracaso, digamos q o 1-p.
aquí, la ocurrencia de una cabeza denota éxito, y la ocurrencia de una cola denota fracaso.probabilidad de obtener una cabeza = 0.5 = probabilidad de obtener una cola ya que solo hay dos posibles resultados.
la función de masa de probabilidad viene dada por: px (1-p)1-x donde x € (0, 1).,
también puede ser escrito como
![]()
Las probabilidades de éxito y el fracaso no necesita ser igualmente probables, como el resultado de una lucha entre el yo y el Enterrador. Está casi seguro de ganar. Así que en este caso la probabilidad de mi éxito es 0.15 mientras que mi fracaso es 0.85
Aquí, la probabilidad de éxito(p) no es lo mismo que la probabilidad de fracaso. Por lo tanto, la siguiente tabla muestra la distribución Bernoulli de nuestra lucha.

Aquí, la probabilidad de éxito = 0.15 y la probabilidad de fracaso = 0.85., El valor esperado es exactamente lo que suena. Si te doy un puñetazo, espero que me des un puñetazo. Básicamente, el valor esperado de cualquier distribución es la media de la distribución., El valor esperado de una variable aleatoria X de una distribución de Bernoulli se encuentra de la siguiente manera:
E(X) = 1*p + 0*(1-p) = p
la varianza de una variable aleatoria de una distribución de bernoulli es:
V(X) = E(X2) – 2 = P – P2 = P(1-P)
hay muchos ejemplos de distribución de Bernoulli, como si va a llover mañana o no, donde la lluvia denota éxito y no Rain denota fracaso y ganar (éxito) o perder (fracaso) el juego.
distribución uniforme
Cuando se rueda un dado justo, los resultados son de 1 a 6., Las probabilidades de obtener estos resultados son igualmente probables y esa es la base de una distribución uniforme. A diferencia de la distribución de Bernoulli, todo el n Número de posibles resultados de una distribución uniforme son igualmente probables.
se dice que una variable X está distribuida uniformemente si la función de densidad es:
![]()
el gráfico de una curva de distribución uniforme se ve como

puede ver que la forma de la curva de distribución uniforme es rectangular, la razón por la que la distribución uniforme se llama distribución rectangular.,
para una distribución uniforme, a y b son los parámetros.
el número de Ramos vendidos diariamente en una florería se distribuye uniformemente con un máximo de 40 y un mínimo de 10.
intentemos calcular la probabilidad de que las ventas diarias caigan entre 15 y 30.
la probabilidad de que las ventas diarias caigan entre 15 y 30 es (30-15)*(1/(40-10)) = 0.5
del mismo modo, la probabilidad de que las ventas diarias son mayores que 20 es = 0.,667
la media y varianza de X siguiendo una distribución uniforme es:
Media -> E(X) = (A+b)/2
varianza -> V(X) = (B-a)2/12
la densidad uniforme estándar tiene parámetros a = 0 y B = 1, por lo que el PDF para la densidad uniforme estándar viene dado por:
![]()
distribución binomial
volvamos al cricket. Supongamos que usted ganó el lanzamiento de hoy y esto indica un evento exitoso. Lanzas de nuevo, pero esta vez perdiste., Si usted gana un lanzamiento hoy, esto no requiere que usted va a ganar el lanzamiento mañana. Asignemos una variable aleatoria, digamos X, al número de veces que ganaste el lanzamiento. ¿Cuál puede ser el valor posible de X? Puede ser cualquier número dependiendo del número de veces que lanzó una moneda.
solo hay dos resultados posibles. Cabeza que denota éxito y cola que denota fracaso. Por lo tanto, la probabilidad de obtener una cabeza = 0.5 y la probabilidad de falla se pueden calcular fácilmente como: q = 1 – p = 0.5.,
una distribución donde solo dos resultados son posibles, como éxito o fracaso, ganancia o pérdida, ganancia o pérdida y donde la probabilidad de éxito y fracaso es la misma para todos los ensayos se denomina distribución Binomial.
los resultados no necesitan ser igualmente probables. ¿Recuerdas el ejemplo de una pelea entre Undertaker y yo? Por lo tanto, si la probabilidad de éxito en un experimento es 0.2 entonces la probabilidad de fracaso se puede calcular fácilmente como q = 1 – 0.2 = 0.8.
cada ensayo es independiente ya que el resultado del lanzamiento anterior no determina ni afecta el resultado del lanzamiento actual., Un experimento con solo dos resultados posibles repetidos n Número de veces se llama binomio. Los parámetros de una distribución binomial son n Y p donde n es el número total de ensayos y p es la probabilidad de éxito en cada ensayo.
sobre la base de la explicación anterior, las propiedades de una distribución Binomial son
- cada ensayo es independiente.
- solo hay dos resultados posibles en un ensayo: un éxito o un fracaso.
- se lleva a cabo un número total de N ensayos idénticos.
- La probabilidad de éxito y fracaso es la misma para todos los ensayos., (Los juicios son idénticos.,
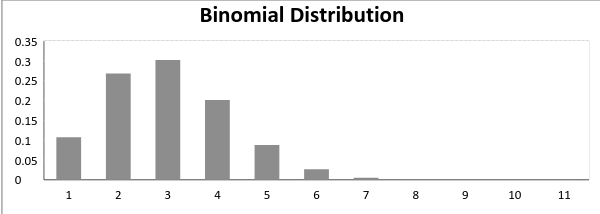
ahora, cuando probabilidad de éxito = probabilidad de fracaso, en tal situación el gráfico de distribución binomial se ve como
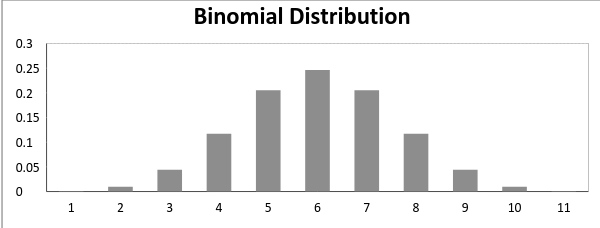
la media y la varianza de una distribución binomial están dadas por:
mean -> µ = n*p
variance -> var(x) = n*p*q
normal distribution
normal la distribución representa el comportamiento de la mayoría de las situaciones en el universo (es por eso que se llama una distribución «normal»., Supongo!). La gran suma de variables aleatorias (pequeñas) a menudo resulta distribuirse normalmente, contribuyendo a su aplicación generalizada. Cualquier distribución se conoce como distribución Normal si tiene las siguientes características:
- La media, mediana y modo de distribución coinciden.
- La Curva de la distribución es en forma de campana y simétrica sobre la línea x = μ.
- el área total bajo La curva es 1.
- exactamente la mitad de los valores están a la izquierda del centro y la otra mitad a la derecha.,
una distribución normal es muy diferente de la distribución Binomial. Sin embargo, si el número de pruebas se acerca al infinito, entonces las formas serán bastante similares.
El PDF de una variable aleatoria X siguiendo una distribución normal está dada por:

la media y La varianza de una variable aleatoria X que se distribuye normalmente está dada por:
Media> E(X) = µ
la Varianza de> Var(X) = σ^2
Aquí, µ (media) y sigma (desviación estándar) son los parámetros.,
el gráfico de una variable aleatoria X ~ N (µ, σ) se muestra a continuación.
Una distribución normal estándar se define como la distribución con media 0 y desviación estándar 1. Para tal caso, el PDF se convierte en:


distribución de Poisson
supongamos que trabaja en un centro de llamadas, aproximadamente cuántas llamadas recibe en un día? Puede ser cualquier número. Ahora, el número entero de llamadas en un centro de llamadas en un día es modelado por distribución de Poisson., Algunos ejemplos más son
- El número de llamadas de emergencia grabadas en un hospital en un día.
- El número de robos reportados en un área en un día.
- El número de clientes que llegan a un salón en una hora.
- El número de suicidios reportados en una ciudad en particular.
- El número de errores de impresión en cada página del libro.
Ahora puedes pensar en muchos ejemplos siguiendo el mismo curso., La distribución de Poisson es aplicable en situaciones donde los eventos ocurren en puntos aleatorios del tiempo y el espacio donde nuestro interés radica solo en el número de ocurrencias del evento.
una distribución se denomina distribución de Poisson cuando las siguientes suposiciones son válidas:
1. Cualquier evento exitoso no debe influir en el resultado de otro evento exitoso.
2. La probabilidad de éxito en un intervalo corto debe ser igual a la probabilidad de éxito en un intervalo más largo.3. La probabilidad de éxito en un intervalo se acerca a cero a medida que el intervalo se hace más pequeño.,ahora, si alguna distribución valida las suposiciones anteriores, entonces es una distribución de Poisson. Algunas notaciones utilizadas en la distribución de Poisson son:
- λ es la velocidad a la que ocurre un evento,
- t es la longitud de un intervalo de tiempo,
- Y X es el número de eventos en ese intervalo de tiempo.
Aquí, X se llama una Variable aleatoria de Poisson y la distribución de probabilidad de X se llama distribución de Poisson.
let µ denotar el número medio de eventos en un intervalo de longitud t. entonces, µ = λ * t.,
el PMF de X después de una distribución de Poisson viene dado por:

la media µ es el parámetro de esta distribución. µ también se define como El λ veces La longitud de ese intervalo. El gráfico de una distribución de Poisson se muestra a continuación:

el gráfico que se muestra a continuación ilustra el cambio en la curva debido al aumento de la media.

es perceptible que la media aumenta, la curva se desplaza hacia la derecha.,
la media y varianza de X siguiendo una distribución de Poisson:
Media -> E(X) = µ
Variance -> Var(X) = µdistribución exponencial
consideremos el ejemplo del centro de llamadas Una vez más. ¿Y el intervalo de tiempo entre las llamadas ? Aquí, la distribución exponencial viene a nuestro rescate. La distribución exponencial modela el intervalo de tiempo entre las llamadas.
Otros ejemplos son:
1. Longitud de tiempo beteeen metro Llegadas,
2., Tiempo entre llegadas a una gasolinera
3. La vida útil de un acondicionador de airela distribución exponencial es ampliamente utilizada para el análisis de supervivencia. Desde la vida esperada de una máquina hasta la vida esperada de un ser humano, la distribución exponencial entrega con éxito el resultado.
se dice que una variable aleatoria X tiene una distribución exponencial con PDF:
f(x) = { λe-λx, x ≥ 0
y parámetro λ>0 que también se llama la tasa.,
para el análisis de supervivencia, λ se denomina tasa de fallo de un dispositivo en cualquier momento t, dado que ha sobrevivido hasta t.
Media y varianza de una variable aleatoria X siguiendo una distribución exponencial:
Media -> E(X) = 1/λ
variance -> var(x) = (1/λ)2
además, cuanto mayor es la tasa, más rápido cae la curva y menor es la tasa, aplana la curva. Esto se explica mejor con el gráfico que se muestra a continuación.,
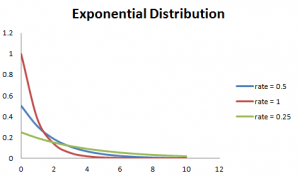
Para facilitar el cálculo, hay algunas fórmulas dadas a continuación.
P{X≤x} = 1 – e-λx, corresponde al área bajo la curva de densidad a la izquierda de x.P{X>x} = e-λx, corresponde al área bajo la curva de densidad a la derecha de x.
P{x1<X≤ x2} = e-λx1 – e-λx2, corresponde al área bajo la curva de densidad entre x1 y x2.
relaciones entre las distribuciones
relación entre Bernoulli y distribución Binomial
1., La distribución de Bernoulli es un caso especial de Distribución Binomial con un solo ensayo.
2. Solo hay dos posibles resultados de una distribución Bernoulli y Binomial, a saber, éxito y fracaso.
3. Tanto Bernoulli como las distribuciones binomiales tienen rutas independientes.
la relación entre Poisson y distribución Binomial
la distribución de Poisson es un caso limitante de distribución binomial bajo las siguientes condiciones:
- El número de ensayos es indefinidamente grande o n → ∞.,
- La probabilidad de éxito para cada ensayo es igual e indefinidamente pequeña o p →0.
- np = λ, es finito.
relación entre distribución normal y Binomial & distribución Normal y de Poisson:
la distribución Normal es otra forma limitante de distribución binomial bajo las siguientes condiciones:
- El número de ensayos es indefinidamente grande, n → ∞.
- tanto p como q no son indefinidamente pequeños.
la distribución normal es también un caso limitante de la distribución de Poisson con el parámetro λ →∞.,
relación entre la distribución exponencial y la distribución de Poisson:
si los tiempos entre eventos aleatorios siguen la distribución exponencial con tasa λ, entonces el número total de eventos en un período de tiempo de longitud T sigue la distribución de Poisson con el parámetro λt.
Pon a prueba tus conocimientos
has llegado hasta aquí. Ahora, ¿eres capaz de responder a las siguientes preguntas? Házmelo saber en los comentarios a continuación!
1. La fórmula para calcular la variable aleatoria normal estándar es:
un. (x+µ) / σ
b. (x-µ) / σ
c. (x-σ) / µ2., En la distribución de Bernoulli, la fórmula para calcular la desviación estándar viene dada por:
a. p (1 – p)
b. SQRT(p(p – 1))
C. SQRT(p(1 – p))3. Para una distribución normal, un aumento en la media:
a. desplazar la curva hacia la izquierda
b.desplazar la curva hacia la derecha
C. aplanar la curva4. La vida útil de una batería se distribuye exponencialmente con λ = 0.05 por hora. La probabilidad de que una batería dure entre 10 y 15 horas es:
a. 0.1341
b.0.1540
c. 0.,0079notas finales
Las distribuciones de probabilidad son frecuentes en muchos sectores, a saber, seguros, Física, Ingeniería, Ciencias de la Computación e incluso Ciencias Sociales, donde los estudiantes de psicología y medicina están utilizando ampliamente las distribuciones de probabilidad. Tiene una aplicación fácil y un uso generalizado. Este artículo destacó seis distribuciones importantes que se observan en la vida cotidiana y explicó su aplicación. Ahora podrás identificar, relacionar y diferenciar entre estas distribuciones.,
Si tiene alguna duda y desea ver más artículos sobre distribuciones, escriba en la sección de comentarios a continuación. Para una descripción más detallada de estas distribuciones, puede consultar este recurso.