Madame Lelica

Eine Sache, die wir mit den Algorithmen in dieser Serie viel tun werden, ist Graph Traversal. Was bedeutet das genau?

Grundsätzlich besteht die Idee darin, dass wir uns im Diagramm von einem Scheitelpunkt zum anderen bewegen und die Eigenschaften ihrer miteinander verbundenen Beziehungen entdecken.

Zwei der am häufigsten verwendeten Algorithmen, die wir häufig verwenden werden, sind: Tiefensuche (DFS) und Breitensuche (BFS).,

Während diese beiden Algorithmen es uns ermöglichen, Graphen zu durchqueren, unterscheiden sie sich auf unterschiedliche Weise. Beginnen wir mit DFS.

DFS nutzt bei der Umsetzung die Philosophie „go deep, head first“. Die Idee ist, dass wir ausgehend von einem anfänglichen Scheitelpunkt (oder Ort) einen Pfad hinuntergehen, bis wir das Ende erreichen, und wenn wir unser Ziel nicht erreichen, kommen wir zurück und gehen einen anderen Weg hinunter.

schauen wir uns ein Beispiel an., Angenommen, wir haben ein gerichtetes Diagramm, das so aussieht:

Nun ist die Idee, dass wir anfangen, bei Vertex s und wir werden gebeten, Vertex t zu finden. Mit DFS, Wir werden einen Pfad erkunden, gehen den ganzen Weg bis zum Ende und wenn wir t nicht finden, dann gehen wir einen anderen Weg hinunter., Hier ist der Prozess:

Also gehen wir hier den Pfad (p1) des ersten benachbarten Scheitelpunkts hinunter und sehen, dass es nicht das Ende ist, weil es einen Pfad zu einem anderen Scheitelpunkt hat., Also gehen wir diesen Pfad hinunter:

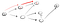
Dies ist eindeutig nicht der Scheitelpunkt, daher haben wir zurück zu gehen, weil wir eine Sackgasse erreicht haben. Da der vorherige Knoten keine Nachbarn mehr hat, kehren wir zu s zurück., Von s, wir gehen zu seinem zweiten benachbarten Knoten:

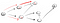
Gehen Sie den Pfad (p2), wir sind konfrontiert mit drei Nachbarn., Da der erste bereits besucht wurde, müssen wir den zweiten runtergehen:

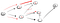
Jetzt haben wir wieder eine Sackgasse erreicht, die nicht der Scheitelpunkt t ist, also müssen wir zurückgehen., Da es einen anderen Nachbarn gibt, der nicht besucht wurde, gehen wir diesen Nachbarpfad hinunter und endlich haben wir den Scheitelpunkt t:

So funktioniert DFS. Gehen Sie einen Pfad hinunter und gehen Sie weiter, bis Sie das Ziel oder eine Sackgasse erreicht haben. Wenn es das Ziel ist, bist du fertig. Wenn nicht, gehen Sie zurück und gehen Sie einen anderen Weg weiter, bis Sie alle Optionen in diesem Pfad ausgeschöpft haben.,

Wir können sehen, dass wir an jedem Scheitelpunkt, den wir besuchen, die gleiche Prozedur ausführen:

Führen Sie für jeden Nachbarn des Scheitelpunkts ein DFS durch

Da dies bei jedem Schritt die gleiche Prozedur erfordert, müssen wir die Rekursion verwenden, um diesen Algorithmus zu implementieren.

Hier ist der Code in JavaScript:

Hinweis: Mit diesem speziellen DFS-Algorithmus können wir feststellen, ob es möglich ist, von einem Ort zum anderen zu gelangen., DFS kann auf verschiedene Arten verwendet werden und es kann subtile Änderungen am obigen Algorithmus geben. Das allgemeine Konzept bleibt jedoch gleich.

Analyse von DFS

Nun analysieren wir diesen Algorithmus. Da wir jeden Nachbarn des Knotens durchlaufen und die besuchten ignorieren, haben wir eine Laufzeit von O(V + E).

Eine kurze Erklärung, was genau V+E bedeutet:

V repräsentiert die Gesamtzahl der Eckpunkte. E stellt die Gesamtzahl der Kanten dar. Jeder Scheitelpunkt hat eine Anzahl von Kanten.,
Während es scheinen mag, dass Sie geführt werden, zu glauben, dass es V•E anstelle von V + E, lassen Sie uns darüber nachdenken, was V• * * E genau bedeutet.

Damit etwas V•E ist, bedeutet dies, dass wir für jeden Scheitelpunkt alle Kanten im Diagramm betrachten müssen, unabhängig davon, ob diese Kanten mit diesem bestimmten Scheitelpunkt verbunden sind oder nicht.

Während andererseits V + E bedeutet, dass wir für jeden Scheitelpunkt nur die Anzahl der Kanten betrachten, die sich auf diesen Scheitelpunkt beziehen. Erinnern Sie sich aus dem vorherigen Beitrag, dass der Platz, den wir für die Adjazenzliste einnehmen, O(V + E) ist., Jeder Scheitelpunkt hat eine Anzahl von Kanten, und im schlimmsten Fall hätten wir, wenn wir DFS auf jedem Scheitelpunkt ausführen würden, O(V) – Arbeit ausgeführt und alle Kanten der Scheitelpunkte untersucht, dh O(E). Sobald wir uns die Anzahl der Eckpunkte angesehen haben, hätten wir uns auch insgesamt E Kanten angesehen. Daher ist es V + E.

Da DFS jetzt für jeden Scheitelpunkt eine Rekursion verwendet, bedeutet dies, dass ein Stapel verwendet wird (weshalb er aufgerufen wird ein Stapelüberlauffehler, wenn Sie auf einen unendlichen rekursiven Aufruf stoßen). Daher ist die Raumkomplexität O (V).,

Nun wollen wir sehen, wie sich die Breitensuche unterscheidet.

Breite-Zuerst-Suche

Breadth-First Search (BFS) folgt die „go wide, bird‘ s-eye-view“ – Philosophie. Was das im Grunde bedeutet, ist, dass BFS, anstatt bis zum Ende einen Pfad ganz nach unten zu gehen, jeweils einen Nachbarn zu seinem Ziel bewegt., Schauen wir uns an, was das bedeutet:

Anstatt also nur den ganzen Weg seinen ersten Nachbarn hinunterzugehen, würde BFS zuerst alle Nachbarn von s besuchen und dann die Nachbarn dieser Nachbarn und so weiter besuchen, bis es t erreicht.,fd17d“>