Wahrscheinlichkeitsverteilung / Arten von Verteilungen

Einführung

Willkommen in der Welt der Wahrscheinlichkeit in der Datenwissenschaft! Lassen Sie mich die Dinge mit einem intuitiven Beispiel beginnen.

Angenommen, Sie sind Lehrer an einer Universität. Nachdem Sie eine Woche lang die Aufgaben überprüft hatten, haben Sie alle Schüler benotet. Sie gaben diese abgestuften Papiere zu einem Dateneingabe Kerl in der Universität und ihm sagen, eine Tabelle mit den Noten aller Studenten zu erstellen., Aber der Typ speichert nur die Noten und nicht die entsprechenden Schüler.

Er hat einen weiteren Fehler gemacht, er hat ein paar Einträge in Eile verpasst und wir haben keine Ahnung, wessen Noten fehlen. Lass uns einen Weg finden, das zu lösen.

Eine Möglichkeit besteht darin, die Noten zu visualisieren und zu sehen, ob Sie einen Trend in den Daten finden können.

Das Diagramm, das Sie zeichnen, wird als Frequenzverteilung der Daten bezeichnet. Sie sehen, dass es eine glatte kurvenartige Struktur gibt, die unsere Daten definiert, aber bemerken Sie eine Anomalie?, Wir haben eine ungewöhnlich niedrige Frequenz in einem bestimmten Punktebereich. Die beste Vermutung wäre also, fehlende Werte zu haben, die die Delle in der Verteilung entfernen.

So würden Sie versuchen, ein reales Problem mithilfe der Datenanalyse zu lösen. Für jeden Datenwissenschaftler, Studenten oder Praktiker ist die Verteilung ein Muss. Es bietet die Grundlage für Analysen und inferenzielle Statistiken.

Während das Konzept der Wahrscheinlichkeit uns die mathematischen Berechnungen gibt, helfen uns Verteilungen tatsächlich zu visualisieren, was darunter passiert.,

In diesem Artikel, habe ich behandelt einige wichtige Wahrscheinlichkeitsverteilungen erläutert werden, der in einem klaren sowie umfassende Art und Weise.

Hinweis: Dieser Artikel setzt voraus, dass Sie Grundkenntnisse der Wahrscheinlichkeit haben. Wenn nicht, können Sie diese Wahrscheinlichkeitsverteilungen verweisen.,

Inhaltsverzeichnis

Gemeinsame Datentypen
Verteilungsarten
1. Bernoulli-Verteilung
2. Gleichmäßige Verteilung
3. Binomialverteilung
4. Normalverteilung
5. Poisson-Verteilung
6. Exponentialverteilung
Beziehungen zwischen den Verteilungen
Testen Sie Ihr Wissen!

Allgemeine Datentypen

Bevor wir zur Erklärung der Verteilungen übergehen, wollen wir sehen, auf welche Art von Daten wir stoßen können. Die Daten können diskret oder kontinuierlich sein.,

Diskrete Daten können, wie der Name schon sagt, nur angegebene Werte annehmen. Wenn Sie beispielsweise einen Würfel rollen, sind die möglichen Ergebnisse 1, 2, 3, 4, 5 oder 6 und nicht 1,5 oder 2,45.

Kontinuierliche Daten können einen beliebigen Wert innerhalb eines bestimmten Bereichs annehmen. Der Bereich kann endlich oder unendlich sein. Zum Beispiel das Gewicht oder die Größe eines Mädchens, die Länge der Straße. Das Gewicht eines Mädchens kann einen beliebigen Wert von 54 kg oder 54,5 kg oder 54.5436 kg haben.

Beginnen wir nun mit den Distributionstypen.,

Verteilungsarten

Bernoulli-Verteilung

Beginnen wir mit der einfachsten Verteilung, der Bernoulli-Verteilung. Es ist eigentlich einfacher zu verstehen, als es klingt!

Alle Cricket-Junkies da draußen! Wie entscheiden Sie zu Beginn eines Cricket-Spiels, wer Schläger oder Ball wird? Ein Wurf! Es hängt alles davon ab, ob Sie den Wurf gewinnen oder verlieren, oder? Sagen wir, wenn der Wurf zu einem Kopf führt, gewinnen Sie. Sonst verlierst du. Es gibt keine Mitte.

Eine Bernoulli-Verteilung hat nur zwei mögliche Ergebnisse, nämlich 1 (Erfolg) und 0 (Misserfolg) und eine einzige Studie., Die Zufallsvariable X, die eine Bernoulli-Verteilung hat, kann also den Wert 1 mit der Erfolgswahrscheinlichkeit annehmen, sagen wir p, und den Wert 0 mit der Ausfallwahrscheinlichkeit, sagen wir q oder 1-p.

Hier bezeichnet das Auftreten eines Kopfes den Erfolg und das Auftreten eines Schwanzes den Fehler.
Wahrscheinlichkeit, einen Kopf zu bekommen = 0,5 = Wahrscheinlichkeit, einen Schwanz zu bekommen, da es nur zwei mögliche Ergebnisse gibt.

Die Wahrscheinlichkeitsmassenfunktion ist gegeben durch: px (1-p) 1-x wobei x € (0, 1).,
Es kann auch geschrieben werden als

Die Wahrscheinlichkeiten von Erfolg und Misserfolg müssen nicht gleich wahrscheinlich sein, wie das Ergebnis eines Kampfes zwischen mir und Undertaker. Er ist sich ziemlich sicher, zu gewinnen. In diesem Fall beträgt die Erfolgswahrscheinlichkeit 0,15, während mein Misserfolg 0,85

Hier ist die Erfolgswahrscheinlichkeit(p) nicht gleich der Ausfallwahrscheinlichkeit. Die folgende Tabelle zeigt also die Bernoulli-Verteilung unseres Kampfes.

Hier ist die Erfolgswahrscheinlichkeit = 0,15 und die Ausfallwahrscheinlichkeit = 0,85., Der erwartete Wert ist genau das, was es klingt. Wenn ich dich prügele, erwarte ich vielleicht, dass du mich zurückschlägst. Grundsätzlich ist der Erwartungswert einer Verteilung der Mittelwert der Verteilung., Der erwartete Wert einer Zufallsvariablen X aus einer Bernoulli-Verteilung wird wie folgt ermittelt:

E(X) = 1*p + 0*(1 – p) = p

Die Varianz einer Zufallsvariablen aus einer Bernoulli – Verteilung ist:

V(X) = E(X2)-2 = p-p2 = p(1-p)Es gibt viele Beispiele für die Bernoulli-Verteilung, z. B. ob es morgen regnen wird oder nicht, wo Regen Erfolg bedeutet und kein Regen Misserfolg und Gewinn (Erfolg) oder Verlust (Misserfolg) des Spiels bedeutet.

Gleichmäßige Verteilung

Wenn Sie einen fairen Würfel rollen, sind die Ergebnisse 1 bis 6., Die Wahrscheinlichkeiten, diese Ergebnisse zu erzielen, sind gleichermaßen wahrscheinlich, und dies ist die Grundlage für eine einheitliche Verteilung. Im Gegensatz zur Bernoulli-Verteilung sind alle n möglichen Ergebnisse einer einheitlichen Verteilung gleich wahrscheinlich.

Eine Variable X soll gleichmäßig verteilt sein, wenn die Dichtefunktion lautet:

Der Graph einer gleichmäßigen Verteilungskurve sieht aus wie

Sie können sehen, dass die Form der gleichmäßigen Verteilungskurve rechteckig ist.,

Für eine gleichmäßige Verteilung sind a und b die Parameter.

Die Anzahl der Blumensträuße, die täglich in einem Blumenladen verkauft werden, ist mit maximal 40 und mindestens 10 gleichmäßig verteilt.

Versuchen wir, die Wahrscheinlichkeit zu berechnen, dass der tägliche Umsatz zwischen 15 und 30 fällt.

Die Wahrscheinlichkeit, dass der tägliche Umsatz zwischen 15 und 30 fällt, ist (30-15)*(1/(40-10)) = 0.5

In ähnlicher Weise ist die Wahrscheinlichkeit, dass der tägliche Umsatz größer als 20 ist = 0.,667

Der Mittelwert und die Varianz von X, die einer gleichmäßigen Verteilung folgen, ist:

Mittelwert -> E(X) = (a+b)/2

Varianz -> V(X) = (b-a)2/12

Die einheitliche Standarddichte hat die Parameter a = 0 und b = 1, so dass das PDF für die einheitliche Standarddichte gegeben durch:

Binomialverteilung

Kehren wir zum Cricket zurück. Angenommen, Sie haben heute den Wurf gewonnen und dies deutet auf ein erfolgreiches Ereignis hin. Sie werfen wieder, aber Sie verloren dieses Mal., Wenn Sie heute einen Wurf gewinnen, erfordert dies nicht, dass Sie morgen den Wurf gewinnen. Weisen wir eine Zufallsvariable zu, z. B. X, wie oft Sie den Wurf gewonnen haben. Was kann der mögliche Wert von X? Es kann eine beliebige Zahl sein, abhängig davon, wie oft Sie eine Münze geworfen haben.

Es gibt nur zwei mögliche Ergebnisse. Kopf bezeichnet Erfolg und Schwanz bezeichnet Misserfolg. Daher kann die Wahrscheinlichkeit, einen Kopf = 0,5 zu erhalten, und die Ausfallwahrscheinlichkeit leicht berechnet werden als: q = 1 – p = 0,5.,

Eine Verteilung, bei der nur zwei Ergebnisse möglich sind, z. B. Erfolg oder Misserfolg, Gewinn oder Verlust, Gewinn oder Verlust, und bei der die Wahrscheinlichkeit von Erfolg und Misserfolg für alle Versuche gleich ist, wird als Binomialverteilung bezeichnet.

Die Ergebnisse müssen nicht gleich wahrscheinlich sein. Erinnern Sie sich an das Beispiel eines Kampfes zwischen mir und Undertaker? Wenn also die Erfolgswahrscheinlichkeit in einem Experiment 0,2 beträgt, kann die Ausfallwahrscheinlichkeit leicht als q = 1 – 0,2 = 0,8 berechnet werden.

Jede Studie ist unabhängig, da das Ergebnis des vorherigen Wurfs das Ergebnis des aktuellen Wurfs nicht bestimmt oder beeinflusst., Ein Experiment mit nur zwei möglichen Ergebnissen, das n-mal wiederholt wird, wird als Binom bezeichnet. Die Parameter einer Binomialverteilung sind n und p wobei n die Gesamtzahl der Versuche und p die Erfolgswahrscheinlichkeit in jeder Studie ist.

Auf der Grundlage der obigen Erklärung sind die Eigenschaften einer Binomialverteilung

Jede Studie ist unabhängig.
Es gibt nur zwei mögliche Ergebnisse in einer Studie – entweder ein Erfolg oder ein Misserfolg.
Insgesamt werden n identische Versuche durchgeführt.
Die Wahrscheinlichkeit von Erfolg und Misserfolg ist für alle Versuche gleich., (Versuche sind identisch.,

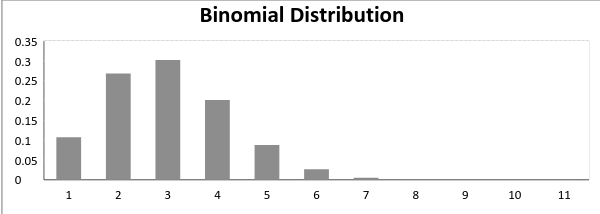
Nun, wenn Erfolgswahrscheinlichkeit = Ausfallwahrscheinlichkeit, sieht der Graph der Binomialverteilung in einer solchen Situation aus wie

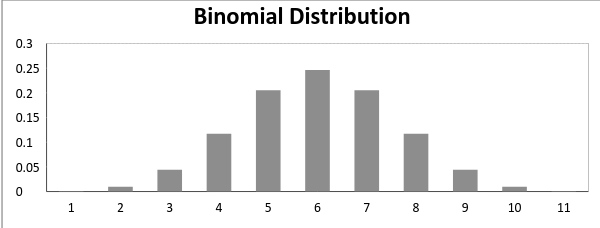
Der Mittelwert und die Varianz einer Binomialverteilung sind gegeben durch:

Mean -> µ = n*p

Varianz -> Var(X) = n*p*q

Normalverteilung

Normalverteilung repräsentiert das Verhalten der meisten Situationen im Universum (Deshalb wird es als „Normalverteilung“ bezeichnet., Ich schätze!). Die große Summe von (kleinen) Zufallsvariablen erweist sich oft als normal verteilt und trägt zu ihrer weit verbreiteten Anwendung bei. Jede Verteilung wird als Normalverteilung bezeichnet, wenn sie die folgenden Eigenschaften aufweist:
1. Der Mittelwert, der Median und die Art der Verteilung stimmen überein.
2. Die Verteilungskurve ist glockenförmig und symmetrisch um die Linie x=μ.
3. Die Gesamtfläche unter der Kurve ist 1.
4. Genau die Hälfte der Werte befindet sich links von der Mitte und die andere Hälfte rechts.,
Eine Normalverteilung unterscheidet sich stark von der Binomialverteilung. Wenn sich jedoch die Anzahl der Versuche der Unendlichkeit nähert, sind die Formen ziemlich ähnlich.

Der Mittelwert einer Zufallsvariablen X nach einer Normalverteilung ist gegeben durch:

Der Mittelwert und die Varianz einer normalverteilten Zufallsvariablen X sind gegeben durch:

Mittelwert -> E(X) = µ

Varianz -> Var(X) = σ^2

Hier sind µ (Mittelwert) und σ (Standardabweichung) die Parameter.,
Der graph einer Zufallsvariablen X ~ N (µ, σ) ist unten dargestellt.

Als Verteilung mit Mittelwert 0 und Standardabweichung 1 ist eine Standardnormalverteilung definiert. Für einen solchen Fall wird das PDF:

Poisson Distribution

Angenommen, Sie arbeiten in einem Callcenter, ungefähr wie viele Anrufe erhalten Sie an einem Tag? Es kann eine beliebige Zahl sein. Jetzt wird die gesamte Anzahl der Anrufe in einem Callcenter an einem Tag durch Poisson Verteilung modelliert., Einige weitere Beispiele sind
1. Die Anzahl der Notrufe, die an einem Tag in einem Krankenhaus aufgezeichnet wurden.
2. Die Anzahl der Diebstähle, die an einem Tag in einem Gebiet gemeldet wurden.
3. Die Anzahl der Kunden, die in einer Stunde in einem Salon ankommen.
4. Die Anzahl der in einer bestimmten Stadt gemeldeten Selbstmorde.
5. Die Anzahl der Druckfehler auf jeder Seite des Buches.
Sie können sich jetzt viele Beispiele vorstellen, die demselben Kurs folgen., Die Poisson-Verteilung ist in Situationen anwendbar, in denen Ereignisse an zufälligen Zeit-und Raumpunkten auftreten, an denen unser Interesse nur in der Anzahl der Ereignisse des Ereignisses liegt.

Eine Verteilung wird Poisson-Verteilung genannt, wenn die folgenden Annahmen gültig sind:

1. Jede erfolgreiche Veranstaltung sollte den Ausgang einer anderen erfolgreichen Veranstaltung nicht beeinflussen.
2. Die Erfolgswahrscheinlichkeit über ein kurzes Intervall muss der Erfolgswahrscheinlichkeit über ein längeres Intervall entsprechen.
3. Die Erfolgswahrscheinlichkeit in einem Intervall nähert sich Null, wenn das Intervall kleiner wird.,

Wenn nun eine Verteilung die obigen Annahmen bestätigt, handelt es sich um eine Poisson-Verteilung. Einige in der Poisson-Verteilung verwendete Notationen sind:
- λ ist die Geschwindigkeit, mit der ein Ereignis auftritt,
- t ist die Länge eines Zeitintervalls,
- Und X ist die Anzahl der Ereignisse in diesem Zeitintervall.
Hier wird X als Poisson-Zufallsvariable und die Wahrscheinlichkeitsverteilung von X als Poisson-Verteilung bezeichnet.

Lassen Sie µ die mittlere Anzahl von Ereignissen in einem Intervall der Länge t bezeichnen.,

Der PMF von X nach einer Poisson-Verteilung ist gegeben durch:

Der Mittelwert µ ist der Parameter dieser Verteilung. µ ist auch definiert als die λ-fache Länge dieses Intervalls. Das Diagramm einer Poisson-Verteilung ist unten dargestellt:

Das unten gezeigte Diagramm veranschaulicht die Verschiebung der Kurve aufgrund einer Erhöhung des Mittelwerts.

Mit zunehmendem Mittelwert verschiebt sich die Kurve nach rechts.,

Der Mittelwert und die Varianz von X nach einer Poisson-Verteilung:

Mean -> E(X) = µ
Variance -> Var(X) = µ

Exponentialverteilung

Betrachten wir das Callcenter-Beispiel noch einmal. Was ist mit dem Zeitintervall zwischen den Anrufen ? Hier kommt die exponentielle Verteilung zu unserer Rettung. Die Exponentialverteilung modelliert das Zeitintervall zwischen den Aufrufen.

Weitere Beispiele sind:

1. Länge der Zeit beteen U-Bahn-Ankünfte,
2., Länge der Zeit zwischen der Ankunft an einer Tankstelle
3. Die Lebensdauer einer Klimaanlage

Exponentialverteilung ist für die Überlebensanalyse weit verbreitet. Von der erwarteten Lebensdauer einer Maschine bis zur erwarteten Lebensdauer eines Menschen liefert die Exponentialverteilung erfolgreich das Ergebnis.

Eine Zufallsvariable X soll eine Exponentialverteilung mit PDF haben:

f(x) = { λe-λx, x ≥ 0

und Parameter λ>0 was auch als rate bezeichnet wird.,

Für die Überlebensanalyse wird λ jederzeit als Ausfallrate eines Gerätes t bezeichnet, da es bis t überlebt hat.

Mittelwert und Varianz einer Zufallsvariablen X nach einer Exponentialverteilung:

Mittelwert -> E(X) = 1/λ

Varianz -> Var(X) = (1/λ)2

Je größer die Rate, desto schneller fällt die Kurve und desto niedriger die Rate, flacher die Kurve. Dies wird besser mit der unten gezeigten Grafik erklärt.,

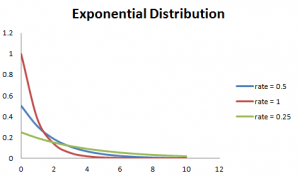
Um die Berechnung zu erleichtern, gibt es unten einige Formeln.
P{X≤x} = 1 – e-λx, entspricht der Fläche unter der Dichtekurve links von x.

P{X>x} = e-λx, entspricht der Fläche unter der Dichtekurve rechts von x.

P{x1<X≤ x2} = e-λx1 – e-λx2, entspricht der Fläche unter der Dichtekurve unter der Dichtekurve zwischen x1 und x2.

Beziehungen zwischen den Verteilungen

Beziehung zwischen Bernoulli und Binomialverteilung

1., Die Bernoulli-Verteilung ist ein Sonderfall der Binomialverteilung mit einer einzigen Studie.

2. Es gibt nur zwei mögliche Ergebnisse einer Bernoulli-und Binomialverteilung, nämlich Erfolg und Misserfolg.

3. Sowohl Bernoulli als auch Binomialverteilungen haben unabhängige Trails.

Beziehung zwischen Poisson und Binomialverteilung

Die Poisson-Verteilung ist ein limitierender Fall der Binomialverteilung unter den folgenden Bedingungen:
1. Die Anzahl der Versuche ist unbegrenzt groß oder n → ∞.,
2. Die Erfolgswahrscheinlichkeit für jede Studie ist gleich und unbegrenzt klein oder p →0.
3. np = λ, endlich ist.
Beziehung zwischen Normal – und Binomialverteilung & Normal-und Poisson-Verteilung:

Normalverteilung ist eine weitere limitierende Form der Binomialverteilung unter den folgenden Bedingungen:
1. Die Anzahl der Versuche ist unbegrenzt groß, n → ∞.
2. Sowohl p als auch q sind nicht unbegrenzt klein.
Die Normalverteilung ist auch ein limitierender Fall der Poisson-Verteilung mit dem Parameter λ →∞.,

Beziehung zwischen exponentieller und Poisson-Verteilung:

Wenn die Zeiten zwischen zufälligen Ereignissen der Exponentialverteilung mit der Rate λ folgen, folgt die Gesamtzahl der Ereignisse in einem Zeitraum der Länge t der Poisson-Verteilung mit dem Parameter λt.

Teste dein Wissen

So weit bist du gekommen. Können Sie nun die folgenden Fragen beantworten? Lass es mich in den Kommentaren unten wissen!

1. Die Formel zur Berechnung der standard-normalverteilte Zufallsvariable ist:

ein. (x+µ) / σ
b. (x-µ) / σ
c. (x-σ) / µ

2., In der Bernoulli-Verteilung ist die Formel zur Berechnung der Standardabweichung gegeben durch:

a. p (1-p)
b. SQRT(p(p – 1))
c. SQRT(p (1 – p))

3. Für eine Normalverteilung wird eine Erhöhung des Mittelwerts:

a. Verschieben Sie die Kurve nach links
b. Verschieben Sie die Kurve nach rechts
c. Glätten Sie die Kurve

4. Die Lebensdauer einer Batterie wird exponentiell mit λ = 0,05 pro Stunde verteilt. Die Wahrscheinlichkeit, dass eine Batterie zwischen 10 und 15 Stunden hält, ist:

a. 0. 1341
b. 0. 1540
c. 0.,0079

Endnoten

Wahrscheinlichkeitsverteilungen sind in vielen Sektoren weit verbreitet, nämlich in den Bereichen Versicherung, Physik, Ingenieurwesen, Informatik und sogar Sozialwissenschaften, wobei die Studenten der Psychologie und Medizin häufig Wahrscheinlichkeitsverteilungen verwenden. Es hat eine einfache Anwendung und weit verbreitete Verwendung. Dieser Artikel hob sechs wichtige Verteilungen hervor, die im täglichen Leben beobachtet werden, und erläuterte deren Anwendung. Jetzt können Sie diese Verteilungen identifizieren, zuordnen und unterscheiden.,

Wenn Sie Zweifel haben und weitere Artikel zu Distributionen sehen möchten, schreiben Sie bitte in den Kommentarbereich unten. Für ein detaillierteres Aufschreiben dieser Distributionen können Sie auf diese Ressource verweisen.