På denne side skitserer vi de tre principper, du skal forstå vedrørende seriekredsløb:
- strøm: mængden af strøm er den samme gennem enhver komponent i et seriekredsløb.
- modstand: den samlede modstand af ethvert seriekredsløb er lig med summen af de individuelle modstande.
- spænding: forsyningsspændingen i et seriekredsløb er lig med summen af de individuelle spændingsfald.,
lad os se på nogle eksempler på seriekredsløb, der demonstrerer disse principper.
Vi vil starte med en række kredsløb, der består af tre modstande og et enkelt batteri:

Det første princip for at forstå, om serien kredsløb er som følger:
Den mængde strøm, der i en serie kredsløb, er den samme gennem alle komponent i kredsløbet.
dette skyldes, at der kun er en sti til strømstrøm i et seriekredsløb., Da elektrisk ladning strømmer gennem ledere som kugler i et rør, skal strømningshastigheden (marmorhastighed) på ethvert tidspunkt i kredsløbet (rør) på et bestemt tidspunkt være ens.
brug af Ohms lov i seriekredsløb
fra den måde, hvorpå 9-volt-batteriet er arrangeret, kan vi fortælle, at strømmen i dette kredsløb vil strømme i urets retning, fra punkt 1 til 2 til 3 til 4 og tilbage til 1. Vi har dog en kilde til spænding og tre modstande. Hvordan bruger vi Ohms lov her?,
en vigtig advarsel til Ohms lov er, at alle mængder (spænding, strøm, modstand og strøm) skal forholde sig til hinanden med hensyn til de samme to punkter i et kredsløb. Vi kan se dette koncept i aktion i eksemplet med enkelt modstandskredsløb nedenfor.,
ved Hjælp af Ohm ‘ s Lov i et Simpelt, Enkelt Modstand Kredsløb
Med en enkelt-batteri, single-modstand kredsløb, kunne vi nemt kan beregne hvilken som helst mængde, fordi de alle anvendes til de samme to punkter i kredsløb:


Siden punkt 1 og 2 er forbundet sammen med ledninger af ringe modstand, som er punkt 3 og 4, kan vi sige, at punkt 1 er elektrisk fælles for punkt 2, og punkt 3 er elektrisk fælles punkt 4., Da vi ved, at vi har 9 volt electromotive force mellem punkt 1 og 4 (lige over batteriet), og siden punkt 2 er fælles for punkt 1 og punkt 3 er fælles for punkt 4, skal vi også have 9 volt mellem punkt 2 og 3 (direkte over modstanden).
derfor kan vi anvende Ohms lov (i = E / R) på strømmen gennem modstanden, fordi vi kender spændingen (e) over modstanden og modstanden (R) for den modstand. Alle udtryk (e, i, R) gælder for de samme to punkter i kredsløbet, til den samme modstand, så vi kan bruge Ohms Lovformel uden forbehold.,
brug af Ohms lov i kredsløb med flere modstande
i kredsløb, der indeholder mere end en modstand, skal vi være forsigtige med, hvordan vi anvender Ohms lov. I tremodstandseksemplet nedenfor ved vi, at vi har 9 volt mellem punkterne 1 og 4, hvilket er mængden af elektromotorisk kraft, der driver strømmen gennem seriekombinationen af R1, R2 og R3. Vi kan dog ikke tage værdien på 9 volt og dividere den med 3k, 10k eller 5k Ω for at forsøge at finde en nuværende værdi, fordi vi ikke ved, hvor meget spænding der er på tværs af en af disse modstande, individuelt.,

tallet på 9 volt er en samlet mængde for hele kredsløbet, mens tallene på 3k, 10k og 5k Ω er individuelle mængder for individuelle modstande. Hvis vi skulle sætte et tal for total spænding i en Ohms Lovligning med et tal for individuel modstand, ville resultatet ikke forholde sig nøjagtigt til nogen mængde i det virkelige kredsløb.,
For R1, Ohm ‘ s Lov, der vedrører mængden af spænding over R1 med strøm gennem R1, da R1 er modstanden, 3kΩ:

Men, da vi ikke kender den spænding over R1 (kun den samlede spænding, der leveres af batteriet på tværs af de tre-modstand serie kombination) og vi kender ikke strøm gennem R1, vi kan ikke gøre noget beregninger med enten formel. Det samme gælder for R2 og R3: vi kan anvende Ohms Lov ligninger, hvis og kun, hvis alle betingelser er repræsentative for deres respektive mængder mellem de samme to punkter i kredsløbet.,
Så hvad kan vi gøre? Vi kender spændingen af kilden (9 volt) anvendt på tværs af seriekombinationen af R1, R2 og R3, og vi kender modstanden for hver modstand, men da disse mængder ikke er i samme sammenhæng, kan vi ikke bruge Ohms lov til at bestemme kredsløbsstrømmen. Hvis vi kun vidste, hvad den samlede modstand var for kredsløbet: så kunne vi beregne den samlede strøm med vores tal for total spænding (i=E/R).,
Kombinere Flere Modstande til en Tilsvarende Samlede Modstand
Dette bringer os til det andet princip-serie kredsløb:
Den samlede modstand af nogen serie kredsløb er lig med summen af de enkelte modstande.
dette skal give intuitiv mening: jo flere modstande i serie, som strømmen skal strømme igennem, jo vanskeligere vil det være for strømmen at strømme.,
I eksemplet problem, vi havde en 3 kΩ, 10 kΩ, og 5 kΩ modstande i serie, hvilket giver os et samlet modstand af 18 kΩ:

I det væsentlige, har vi beregnet de tilsvarende modstand af R1, R2 og R3 kombineret.,oltages ved Hjælp af Ohm ‘ s Lov
Vide, at nuværende er lige gennem alle komponenter af en række kredsløb (og det har vi lige konstateret den nuværende gennem batteriet), kan vi gå tilbage til vores oprindelige kredsløb skematisk og bemærk den nuværende gennem hver komponent:
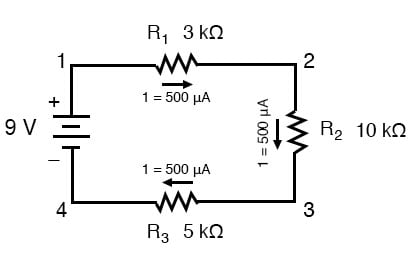
Nu, at vi kender mængden af strøm gennem hver enkelt modstand, vi kan bruge Ohms Lov at bestemme spændingsfaldet over hver enkelt at anvende Ohms Lov i dens rette sammenhæng):

Bemærk spændingen falder over hver enkelt modstand, og hvordan summen af spændingen falder (1.,5 + 5 + 2.5) er lig med batteriet (forsyning) spænding: 9 volt.
dette er det tredje princip i seriekredsløb:
forsyningsspændingen i et seriekredsløb er lig med summen af de individuelle spændingsfald.
analyse af enkle seriekredsløb med “Tabelmetoden” og Ohms lov
den metode, vi lige brugte til at analysere dette enkle seriekredsløb, kan imidlertid strømlines for bedre forståelse., Ved at bruge en tabel til at liste alle spænding, strøm og modstand i kredsløbet, bliver det meget nemt at se, hvilke af disse mængder kan være korrekt, der er relateret Ohm ‘ s Lov ligning:

regel med en sådan tabel er at anvende Ohms Lov kun at værdierne inden for hver lodret kolonne. For eksempel, ER1 kun med IR1 og R1; ER2 kun med IR2 og R2, osv., Du begynder din analyse ved at udfylde de dele af tabellen, der er givet til dig fra begyndelsen:

Som du kan se på placeringen af data, kan vi ikke anvende den 9 volt af ET (total spænding) til nogen af de modstande (R1, R2 eller R3) i Ohm ‘ s Lov, formel, fordi de er i forskellige kolonner. 9 volt batterispænding påføres ikke direkte over R1, R2 eller R3. Vi kan dog bruge vores “regler” for seriekredsløb til at udfylde tomme pletter på en vandret række.,t 500 µA:

Så, vel vidende, at strømmen er fordelt ligeligt af alle komponenter af en række kredsløb (en anden “regel” i serien kredsløb), kan vi fylde i strømme for hver modstand fra det nuværende tal kun beregnet:

Endelig, vi kan bruge Ohms Lov at bestemme spændingsfaldet over hver enkelt modstand, én kolonne ad gangen:

Verificere Beregninger med Edb-Analyse (SPICE)
Bare for sjov, vi kan bruge en computer til at analysere dette meget samme kredsløb automatisk., Det vil være en god måde at verificere vores beregninger og også blive mere fortrolig med computeranalyse. Først skal vi beskrive kredsløbet til computeren i et format, der kan genkendes af Soft .aren.SPICE-programmet, vi bruger, kræver, at alle elektrisk unikke punkter i et kredsløb nummereres, og komponentplacering forstås af hvilke af de nummererede punkter eller “noder”, de deler. For klarhedens skyld nummererede jeg de fire hjørner af vores eksempelkredsløb 1 til 4., SPICE, men kræver, at der skal være en knude nul, et eller andet sted i kredsløbet, så jeg vil gentegne kredsløb, skiftende nummerrækkefølgen lidt:

Alt hvad jeg har gjort her, er at re-nummererede det nederste venstre hjørne af kredsløb 0 i stedet for 4. Nu Kan jeg indtaste flere tekstlinjer i en computerfil, der beskriver kredsløbet med hensyn til SPICE vil forstå, komplet med et par ekstra kodelinjer, der dirigerer programmet til at vise spænding og aktuelle data til vores oplevelse., Denne fil på computeren, der er kendt som netlist i SPICE terminologi:
series circuit v1 1 0 r1 1 2 3k r2 2 3 10k r3 3 0 5k .dc v1 9 9 1 .print dc v(1,2) v(2,3) v(3,0) .end
Nu, er alt jeg har at gøre, er at køre SPICE program til at behandle netlist og output resultaterne:
| v1 | v(1,2) | v(2,3) | v(3) | i(v1) |
|---|---|---|---|---|
| 9.000 E+00 | 1.500 E+00 | 5.000 E+00 | 2.500 E+00 | -5.,000E-04 |
Denne udskrift er at fortælle os, batterispændingen er 9 volt, og spændingen falder over R1, R2 og R3 er 1,5 volt, 5 volt, og 2,5 volt, hhv. Spændingsfald over en hvilken som helst komponent i SPICE refereres af nodenumrene komponenten ligger imellem, så V(1,2) refererer spændingen mellem knudepunkter 1 og 2 i kredsløbet, som er de punkter, mellem hvilke R1 er placeret.,
rækkefølgen af knudenumre er vigtig: når SPICE udsender et tal for v(1,2), betragter det polariteten på samme måde som om vi holdt et voltmeter med den røde testledning på node 1 og den sorte testledning på node 2. Vi har også et display, der viser strøm (omend med en negativ værdi) ved 0, 5 milliamps eller 500 mikroamps. Så vores matematiske analyse er blevet retfærdiggjort af computeren. Dette tal fremstår som et negativt tal i KRYDDERIANALYSEN, på grund af en særhed i den måde, SPICE håndterer aktuelle beregninger på.,
sammenfattende defineres et seriekredsløb som kun at have en sti, gennem hvilken strøm kan strømme. Fra denne definition følger tre regler for seriekredsløb: alle komponenter deler den samme strøm; modstande tilføjer lige en større, total modstand; og spændingsfald tilføjer lige en større, total spænding. Alle disse regler finder rod i definitionen af et seriekredsløb. Hvis du forstår denne definition fuldt ud, er reglerne intet andet end fodnoter til definitionen.
anmeldelse:
- komponenter i en serie kredsløb deler den samme strøm: ITotal = I1 = I2 = . . ., I
- er den samlede modstand i et seriekredsløb lig med summen af de individuelle modstande: RTotal = R1 + R2 + . . . Rn
- Total spænding i et seriekredsløb er lig med summen af de individuelle spændingsfald ETotal = E1 + E2 + . . . En
prøv vores Ohms Lovberegner i vores Værktøjssektion.
RELATERET REGNEARK:
- Serie DC Kredsløb Praksis Regneark med Svar Regneark
- Algebraisk Ligning Manipulation for Elektriske Kredsløb Regneark