en ting, som vi vil gøre meget med algoritmerne i denne serie, er graf traversal. Hvad betyder det præcist?
grundlæggende er ideen, at vi bevæger os rundt i grafen fra et hjørne til et andet og opdager egenskaberne ved deres sammenkoblede forhold.to af de mest anvendte algoritmer, som vi bruger meget, er: dybde-første søgning (DFS) og bredde-første søgning (bfs).,mens begge disse algoritmer tillader os at krydse grafer, adskiller de sig på forskellige måder. Lad os starte med DFS.
DFS udnytter “gå dybt, hoved først” filosofi i dens gennemførelse. Ideen er, at vi starter fra et indledende toppunkt (eller sted), vi går ned ad en sti, indtil vi når slutningen, og hvis vi ikke når vores destination, kommer vi tilbage og går ned ad en anden sti.
lad os se på et eksempel., Antag at vi har en orienteret graf, der ligner denne:

Nu ideen er, at vi starter på vertex s, og vi bliver bedt om at finde vertex t. Ved hjælp af DFS, vi kommer til at udforske en sti, gå hele vejen til slutningen, og hvis vi ikke kan finde t, så vi går ned ad en anden vej., Her er processen:

Så her, vi går ned af stien (p1) i første tilstødende vertex, og vi kan se, at det ikke er slutningen, fordi det er en vej mod en anden vinkelspids., Så vi går videre ad den vej:
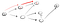
Det er helt klart ikke isse t, så er vi nødt til at gå tilbage, fordi vi nået til en blindgyde. Da den forrige knude ikke har længere naboer, går vi tilbage til s., Fra s, vi går til sin anden nabo node:
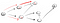
at Gå ned ad den sti (p2), vi er konfronteret med tre naboer., Da den første har allerede været besøgt, er vi nødt til at gå ned til den anden:
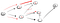
Nu, endnu engang har vi nået en blindgyde, som ikke isse t, så er vi nødt til at gå tilbage., Da der er en anden nabo, der ikke har været besøgt, vi går ad den tilstødende vej, og til sidst fandt vi vertex t:

Dette er, hvordan DFS værker. Gå ned ad en sti og fortsæt, indtil du har nået destinationen eller en blindgyde. Hvis det er destinationen, er du færdig. Hvis det ikke er tilfældet, så gå tilbage og fortsæt ned ad en anden sti, indtil du har udtømt alle muligheder inden for den sti.,
Vi kan se, at vi følger den samme procedure ved hver vertex, at vi besøg:
har en DFS-for hver nabo for vertex
Da dette indebærer, at gøre den samme procedure, som ved hvert skridt, noget siger os, at vi bliver nødt til at bruge rekursion for at gennemføre denne algoritme.
Her er den kode i JavaScript:
Bemærk: Denne specifikke DFS algoritme giver os mulighed for at afgøre, om det er muligt at nå fra et sted til et andet., DFS kan bruges på forskellige måder, og der kan være subtile ændringer i algoritmen ovenfor. Men det generelle koncept forbliver det samme.
analyse af DFS
lad os nu analysere denne algoritme. Da vi krydser gennem hver nabo af noden, og vi ignorerer de besøgte, har vi en runtime på O(V + E).
en hurtig forklaring på præcis, hvad V+E betyder:
v repræsenterer det samlede antal hjørner. E repræsenterer det samlede antal kanter. Hvert hjørne har en række kanter., selvom det kan se ud til, at man kan blive ført til at tro, at det er V•e i stedet for V + e, lad os tænke over, hvad V•E betyder nøjagtigt.
for at noget skal være V•E, ville det betyde, at vi for hvert toppunkt skal se på alle kanterne i grafen, uanset om disse kanter er forbundet med det specifikke toppunkt eller ej.
mens V + E på den anden side betyder, at vi for hvert toppunkt kun ser på antallet af kanter, der vedrører det toppunkt. Husk fra det forrige indlæg, at det rum, vi tager op til adjacency-listen, er o (V + E)., Hvert toppunkt har et antal kanter, og i værste fald, hvis vi skulle køre DFS på hvert toppunkt, ville vi have gjort O(V) arbejde sammen med at udforske alle kanterne af toppunkterne, hvilket er O(E). Når vi har set på alle v antal knudepunkter, vi ville også have set på i alt E kanter. Derfor er det V + E.
nu, da DFS bruger rekursion på hvert toppunkt, betyder det, at der bruges en stak (hvorfor det kaldes en stakoverløbsfejl, når du løber ind i et uendeligt rekursivt opkald). Derfor er rumkompleksiteten O (V).,
lad os nu se, hvordan bredden-første søgning adskiller sig.
bredde-første søgning
bredde-første søgning (bfs) følger filosofien “gå bredt, fugleperspektiv”. Hvad det dybest set betyder er, at i stedet for at gå helt ned ad en sti indtil slutningen, bevæger BFS sig mod sin destination en nabo ad gangen., Lad os se på, hvad det betyder:

Så i stedet for bare at gå hele vejen ned i dens første nabo, BFS ville besøge alle de naboer af s første, og derefter besøge dem, naboer naboer og så videre, indtil det når t.,fd17d”> 

See how different DFS and BFS behave?, Mens jeg kan lide at tro, at DFS kan lide at gå hovedet på, BFS kan lide at se tage det langsomt og observere alt et skridt ad gangen.nu skal et spørgsmål, der skiller sig ud for os, være: “Hvordan ved vi, hvilke naboer der først skal besøge fra S’ S naboer?”
Nå, vi kunne bruge en kø ‘ s first-in-first-out (FIFO) ejendom, hvor vi pop det første hjørne af køen, Tilføj sine ubesøgte naboer til køen, og fortsæt derefter denne proces, indtil køen er enten tom eller det toppunkt, vi tilføjer til det, er det toppunkt, vi har ledt efter.,
lad os Nu se på koden i JavaScript:
Analyser af BFS
Det kan synes som BFS er langsommere. Men hvis du ser nøje på visualiseringerne af både BFS og DFS, vil du opdage, at de faktisk har den samme runtime.
køen sikrer, at højst hvert toppunkt behandles, indtil det når destinationen. Så det betyder i værste fald, at BFS også vil se på alle hjørner og alle kanter.,selvom BFS kan virke langsommere, anses det faktisk hurtigere, fordi hvis vi skulle implementere dem på større grafer, vil du opdage, at DFS spilder meget tid på at gå ned lange stier, der i sidste ende er forkerte. Faktisk bruges BFS ofte i algoritmer til at bestemme den korteste vej fra et hjørne til et andet, men vi vil røre ved dem senere.
så da driftstiderne er de samme, har BFS en runtime på O(V + E), og på grund af brugen af en kø, der højst kan indeholde v-hjørner, har den en rumkompleksitet på O(V).,
analogier til at forlade med
Jeg vil forlade dig med andre måder, som jeg personligt forestiller mig, hvordan DFS og BFS fungerer i håb om, at det også hjælper dig med at huske.
hver gang jeg tænker på DFS, kan jeg godt lide at tænke på noget, der finder den rigtige vej ved at støde på mange døde ender. Normalt ville dette være som en mus, der går gennem en labyrint for at lede efter mad.,ville prøve en vej, finde ud af, at den vej er en blindgyde, drej derefter til en anden vej, og gentag denne proces, indtil det når sit mål:

Og dette er, hvad en forenklet version af processen ville se ud:

Nu for BFS, Jeg har altid forestillet mig det som en krusning.,div>

Meget gerne, hvordan BFS starter ved kilden og besøg på kilden naboer først og derefter går udad ved at besøge deres naboer og så videre:

Resumé
- Dybde-Først Søgning (DFS) og Bredde-Først-Søgning (BFS) er både bruges til at krydse grafer.,
- DFS opkræver en sti, indtil den har udtømt den sti for at finde sit mål, mens BFS krusninger gennem tilstødende hjørner for at finde sit mål.
- DFS bruger en stak, mens BFS bruger en kø.
- både DFS og BFS har en driftstid på O(V + E) og en rumkompleksitet på O (V).begge algoritmer har forskellige filosofier, men deler lige stor betydning for, hvordan vi krydser grafer.