Sandsynlighedsfordeling /typer af distributioner

introduktion

velkommen til Sandsynlighedsverdenen inden for datavidenskab! Lad mig starte tingene med et intuitivt eksempel.Antag, at du er lærer på et universitet. Efter at have tjekket opgaver i en uge, sorterede du alle eleverne. Du gav disse sorterede papirer til en dataindtastnings fyr på universitetet og bad ham om at oprette et regneark, der indeholder karaktererne for alle studerende., Men fyren gemmer kun karaktererne og ikke de tilsvarende studerende.

han lavede en anden bommert, han savnede et par poster i en fart, og vi har ingen ID.om, hvis karakterer mangler. Lad os finde en måde at løse dette på.en måde er, at du visualiserer karaktererne og ser om du kan finde en tendens i dataene.

den Graf, du har plot kaldes frekvensfordelingen af dataene. Du ser, at der er en glat kurve som struktur, der definerer vores data, men bemærker du en anomali?, Vi har en unormalt lav frekvens på et bestemt scoreområde. Så det bedste gæt ville være at have manglende værdier, der fjerner bukken i distributionen.

sådan vil du forsøge at løse et ægte problem ved hjælp af dataanalyse. For enhver dataforsker, en studerende eller en praktiserende læge er distribution et must kno. – koncept. Det giver grundlag for analytics og inferential statistik.

mens begrebet sandsynlighed giver os de matematiske beregninger, distributioner hjælpe os faktisk visualisere, hvad der sker nedenunder.,

i denne artikel har jeg dækket nogle vigtige sandsynlighedsfordelinger, der forklares på en klar og omfattende måde.Bemærk: Denne artikel forudsætter, at du har et grundlæggende kendskab til Sandsynlighed. Hvis ikke, kan du henvise denne sandsynlighedsfordelinger.,

Indholdsfortegnelse

Fælles datatyper
Typer af Distributioner
1. Bernoulli Distribution
2. Uniform Fordeling
3. Binomial Distribution
4. Normal Fordeling
5. Poisson-Fordeling
6. Eksponentiel Fordeling
Forbindelser mellem Distributioner
Test din Viden!

almindelige datatyper

før vi går videre til forklaringen af distributioner, lad os se, hvilken slags data vi kan støde på. Dataene kan være diskrete eller kontinuerlige.,

diskrete Data, som navnet antyder, kan kun tage angivne værdier. For eksempel, når du ruller en terning, er de mulige resultater 1, 2, 3, 4, 5 eller 6 og ikke 1.5 eller 2.45.

kontinuerlige Data kan tage en hvilken som helst værdi inden for et givet område. Området kan være begrænset eller uendeligt. For eksempel, en piges vægt eller højde, længden af vejen. Vægten af en pige kan være en værdi fra 54 kg eller 54,5 kg eller 54.5436 kg.

lad os nu starte med de typer distributioner.,

typer af distributioner

Bernoulli Distribution

lad os starte med den nemmeste distribution, der er Bernoulli Distribution. Det er faktisk lettere at forstå, end det lyder!

alle jer cricket junkies derude! I begyndelsen af enhver cricket-kamp, Hvordan bestemmer du, hvem der skal bat eller bold? Et kast! Det hele afhænger af, om du vinder eller taber kastet, ikke? Lad os sige, hvis kastet resulterer i et hoved, vinder du. Ellers taber du. Der er ingen midtvejs.

en Bernoulli-distribution har kun to mulige resultater, nemlig 1 (succes) og 0 (fiasko) og et enkelt forsøg., Så den stokastiske variabel X, som har en Bernoulli-distribution kan tage værdien 1 med sandsynligheden for succes, siger s, og værdien 0 med sandsynlighed for fiasko, siger, q eller 1-p.

Her, er forekomsten af et hoved, der angiver succes, og forekomsten af en hale betegner fiasko.
Sandsynlighed for at få et hoved = 0.5 = Sandsynlighed for at få en hale, da der kun er to mulige resultater.

sandsynlighedsmassefunktionen er givet ved: P. (1-p)1-where hvor where € (0, 1).,
Det kan også skrives som

sandsynlighederne for succes og fiasko behøver ikke være lige sandsynlige, som resultatet af en kamp mellem mig og Undertaker. Han er temmelig sikker på at vinde. Så i dette tilfælde er sandsynligheden for, at min succes er, 0.15, mens min fiasko er 0.85

Her, er sandsynligheden for succes(p) ikke er den samme som sandsynligheden for fiasko. Så nedenstående diagram viser Bernoulli-fordelingen af vores kamp.

Her, er sandsynligheden for succes = 0.15, og sandsynligheden for fiasko = 0.85., Den forventede værdi er præcis, hvad det lyder. Hvis jeg slår dig, kan jeg forvente, at du slår mig tilbage. Dybest set forventede værdi af enhver fordeling er middelværdien af fordelingen., Den forventede værdi af en stokastisk variabel X fra en Bernoulli-distributionen er fundet som følger:

E(X) = 1*p + 0*(1-p) = p

variansen af en tilfældig variabel fra en bernoulli-distributionen er:

V(X) = E(X2) – 2 = p – p2 = p(1-p)

Der er mange eksempler på Bernoulli-distribution såsom om det bliver regnvejr i morgen eller ej, hvor regnen står for succes og ingen regn angiver, svigt og Vinde (succes), eller at miste (manglende) spil.

ensartet fordeling

Når du ruller en retfærdig matrice, er resultaterne 1 til 6., Sandsynligheden for at få disse resultater er lige så sandsynlige, og det er grundlaget for en ensartet fordeling. I modsætning til Bernoulli Distribution, alle n antallet af mulige resultater af en ensartet fordeling er lige sandsynlige.

En variabel X siges at være jævnt fordelt, hvis tæthedsfunktionen er:

grafen for en ensartet fordeling kurve ligner

Du kan se, at den form for Uniform fordeling kurve er rektangulært, grunden til, at en Ensartet fordeling kaldes rektangulær fordeling.,

for en ensartet fordeling er A og b parametrene.

antallet af buketter, der sælges dagligt i en blomsterbutik, fordeles ensartet med maksimalt 40 og mindst 10.

lad os prøve at beregne sandsynligheden for, at det daglige salg falder mellem 15 og 30.

sandsynligheden for, at det daglige salg falder mellem 15 og 30, er (30-15)*(1/(40-10)) = 0.5

tilsvarende er sandsynligheden for, at det daglige salg er større end 20 = 0.,667

Det er middelværdi og varians af X efter en ensartet fordeling er:

Mean -> E(X) = (a+b)/2

Varians -> V(X) = (b-a)2/12

standard uniform tæthed er parametre a = 0 og b = 1, så PDF-standard for ensartet tæthed givet ved:

Binomial Distribution

Lad os komme tilbage til cricket. Antag at du vandt kastet i dag, og det indikerer en vellykket begivenhed. Du kaster igen, men du tabte denne gang., Hvis du vinder et kast i dag, kræver det ikke, at du vinder kastet i morgen. Lad os tildele en tilfældig variabel, siger X, til det antal gange, du vandt kastet. Hvad kan være den mulige værdi af?? Det kan være et vilkårligt antal afhængigt af antallet af gange, du kastede en mønt.

Der er kun to mulige resultater. Hoved betegner succes og hale betegner fiasko. Derfor kan sandsynligheden for at få et hoved = 0, 5 og sandsynligheden for fiasko let beregnes som: = = 1 – p = 0, 5.,

en distribution, hvor kun to resultater er mulige, såsom succes eller fiasko, gevinst eller tab, sejr eller tab, og hvor sandsynligheden for succes og fiasko er den samme for alle forsøgene kaldes en Binomial Distribution.

resultaterne behøver ikke være lige sandsynlige. Kan du huske eksemplet på en kamp mellem mig og Undertaker? Så hvis sandsynligheden for succes i et eksperiment er 0,2 derefter sandsynligheden for fiasko kan let beregnes som 1 = 1-0,2 = 0,8.

hvert forsøg er uafhængigt, da resultatet af det foregående kast ikke bestemmer eller påvirker resultatet af det aktuelle kast., Et eksperiment med kun to mulige udfald gentaget n antal gange kaldes binomial. Parametrene for en binomial fordeling er n og p hvor n er det samlede antal forsøg, og p er sandsynligheden for succes i hvert forsøg.

på grundlag af ovenstående forklaring er egenskaberne for en Binomial fordeling

hvert forsøg er uafhængigt.
der er kun to mulige resultater i et forsøg – enten en succes eller en fiasko.
der udføres et samlet antal n-identiske forsøg.
sandsynligheden for succes og fiasko er den samme for alle forsøg., (Forsøg er identiske.,

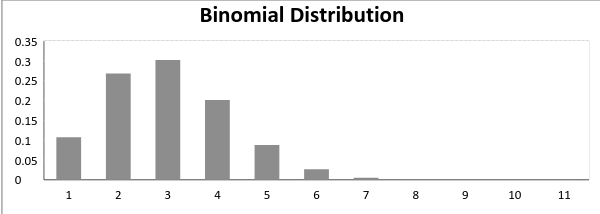
Nu, hvor sandsynligheden for succes = sandsynligheden for svigt, i en sådan situation grafen for binomialfordelingen ligner

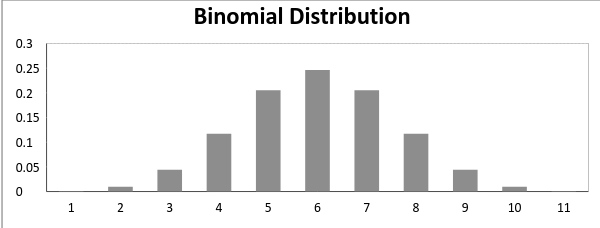
Det er middelværdi og varians af en binomial fordeling er givet ved:

Mean -> μ = n*p

Varians -> Var(X) = n*p*q

Normal Fordeling

Normal fordeling repræsenterer den adfærd, der af de fleste af de situationer i universet (Det er derfor det hedder en “normal” distribution., Jeg gætter!). Den store sum af (små) tilfældige variabler viser sig ofte at være normalt fordelt, hvilket bidrager til dens udbredte anvendelse. Enhver distribution er kendt som Normal distribution, hvis den har følgende egenskaber:
1. distributionens middel, median og tilstand falder sammen.
2. kurven for fordelingen er klokkeformet og symmetrisk omkring linjen= = μ.
3. det samlede areal under kurven er 1.
4. præcis halvdelen af værdierne er til venstre for midten og den anden halvdel til højre.,
en normal fordeling er meget forskellig fra Binomial Distribution. Men hvis antallet af forsøg nærmer sig uendeligt, vil formerne være ret ens.

PDF af en stokastisk variabel X at følge en normal fordeling er givet ved:

middelværdien og variansen af en stokastisk variabel X, som siges at være normalt fordelt, er givet ved:

Mean -> E(X) = µ

Varians -> Var(X) = σ^2

Her, µ (mean) og σ (standard afvigelsen) er de parametre.,
grafen for en tilfældig variabel ~ ~ n (,,)) er vist nedenfor.

en normal normalfordeling defineres som fordelingen med Middel 0 og standardafvigelse 1. For sådan en sag, PDF-bliver:

Poisson-Fordeling

Antag, at du arbejder på et call center, omtrent hvor mange opkald du får på en dag? Det kan være et hvilket som helst nummer. Nu er hele antallet af opkald på et callcenter på en dag modelleret af Poisson distribution., Nogle flere eksempler er
1. antallet af nødopkald optaget på et hospital om dagen.
2. antallet af tyverier rapporteret i et område på en dag.
3. antallet af kunder, der ankommer til en salon om en time.
4. antallet af selvmord rapporteret i en bestemt by.
5. antallet af trykfejl på hver side i bogen.
Du kan nu tænke på mange eksempler efter det samme kursus., Poisson Distribution er anvendelig i situationer, hvor begivenheder forekommer på tilfældige tidspunkter og rum, hvor vores interesse kun ligger i antallet af forekomster af begivenheden.

en distribution kaldes Poisson distribution, når følgende antagelser er gyldige:

1. Enhver vellykket begivenhed bør ikke påvirke resultatet af en anden vellykket begivenhed.
2. Sandsynligheden for succes over et kort interval skal svare til sandsynligheden for succes over et længere interval.
3. Sandsynligheden for succes i et interval nærmer sig nul, da intervallet bliver mindre.,

nu, hvis en distribution validerer ovenstående antagelser, er det en Poisson-distribution. Nogle notationer, der bruges i Poisson-distributionen, er:
- λ er den hastighed, hvormed en begivenhed opstår,
- t er længden af et tidsinterval,
- og And er antallet af begivenheder i det tidsinterval.
Her kaldes Random en Poisson tilfældig variabel, og sandsynlighedsfordelingen af.kaldes Poisson distribution.

lad µ betegne det gennemsnitlige antal hændelser i et interval af længde t. derefter µ = λ*t.,

PMF for pois efter en Poisson-distribution er givet ved:

den gennemsnitlige µ er parameteren for denne distribution. µ er også defineret som interval gange længden af dette interval. Grafen for en Poisson-distribution er vist nedenfor:

grafen vist nedenfor illustrerer skiftet i kurven på grund af stigning i middelværdien.

det er mærkbart, at når gennemsnittet stiger, skifter kurven til højre.,

Det er middelværdi og varians af X følger en Poisson-fordeling:

Mean -> E(X) = µ
Varians -> Var(X) = µ

Eksponentiel Fordeling

Lad os overveje call center eksempel en gang mere. Hvad med tidsintervallet mellem opkaldene ? Her kommer eksponentiel distribution til vores redning. Eksponentiel distribution modellerer tidsintervallet mellem opkaldene.

andre eksempler er:

1. Længde af tid beteeen metro ankomster,
2., Længden af tid mellem ankomster på en tankstation
3. Levetiden for et klimaanlæg

eksponentiel distribution bruges i vid udstrækning til overlevelsesanalyse. Fra en maskines forventede levetid til et menneskes forventede liv leverer eksponentiel distribution med succes resultatet.

En stokastisk variabel X siges at have en eksponentiel fordeling med PDF:

f(x) = { λe-λx, x ≥ 0

og parameter λ>0, hvilket også kaldes sats.,

For overlevelse analyse, λ kaldes fejlrate af en anordning, der på ethvert tidspunkt t, givet at det har overlevet op til t.

Middelværdien og Variansen af en stokastisk variabel X efter en eksponentiel fordeling:

Mean -> E(X) = 1/λ

Varians -> Var(X) = (1/λ)2

Også, at jo større sats, jo hurtigere kurven falder og den lavere sats, fladere kurve. Dette forklares bedre med grafen vist nedenfor.,

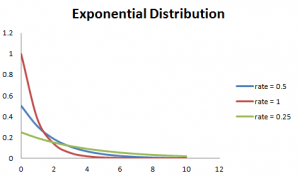
for at lette beregningen er der nogle formler angivet nedenfor.
P{X≤x} = 1 – e-λx, svarer til arealet under tæthed kurve til venstre for x.

P{X>x} = e-λx, svarer til arealet under tæthed kurven til højre for x.

P (x1<X≤ x2} = e-λx1 – e-λx2, svarer til arealet under tæthed kurven mellem x1 og x2.

forholdet mellem distributionerne

forholdet mellem Bernoulli og Binomial Distribution

1., Bernoulli Distribution er et specielt tilfælde af Binomial Distribution med et enkelt forsøg.

2. Der er kun to mulige resultater af en Bernoulli og Binomial fordeling, nemlig succes og fiasko.

3. Både Bernoulli og Binomial distributioner har uafhængige stier.

Forhold mellem Poisson og Binomial Distribution

Poisson-Fordeling er en begrænsning af tilfælde af binomialfordelingen under følgende betingelser:
1. antallet af forsøg er uendeligt store, eller n → ∞.,
2. sandsynligheden for succes for hvert forsøg er den samme og på ubestemt tid lille eller p 0 0.
3. np = λ, er begrænset.
Forhold mellem Normal og Binomial Distribution & Normal og Poisson-Fordeling:

Normal distribution er en anden begrænsning form af binomialfordelingen under følgende betingelser:
1. antallet af forsøg er uendeligt stort, n → ∞.
2. både p og q er ikke på ubestemt tid små.
den normale fordeling er også et begrænsende tilfælde af Poisson distribution med parameteren λ→..,

forholdet mellem eksponentiel og Poisson Distribution:

hvis tiderne mellem tilfældige begivenheder følger eksponentiel distribution med hastighed., følger det samlede antal begivenheder i en tidsperiode af længde t Poisson distribution med parameterentt.

Test din viden

Du er kommet så langt. Nu, er du i stand til at besvare følgende spørgsmål? Lad mig vide i kommentarerne nedenfor!

1. Formlen til beregning af standard normal tilfældig variabel er:

a. (++µ) / b. (–)) / c. (. -))/

2., I Bernoulli-distributionen er formlen til beregning af standardafvigelse givet ved:

a. p (1 – p)
b. s .rt(p(p – 1))
c. s .rt(p(1 – p))

3. For en normal fordeling vil en stigning i middelværdien:

a. skift kurven til venstre
b. skift kurven til højre
c. flad kurven

4. Levetiden af et batteri er eksponentielt fordelt med 0.0 = 0,05 per time. Sandsynligheden for, at et batteri varer mellem 10 og 15 timer, er:

a.0.1341
b.0.1540
c.0.,0079

End Notes

sandsynlighedsfordelinger er udbredt i mange sektorer, nemlig forsikring, fysik, teknik, datalogi og endda samfundsvidenskab, hvor eleverne i psykologi og medicinsk i vid udstrækning bruger sandsynlighedsfordelinger. Det har en nem anvendelse og udbredt brug. Denne artikel fremhævede seks vigtige distributioner, der observeres i det daglige liv og forklarede deres anvendelse. Nu vil du være i stand til at identificere, relatere og differentiere mellem disse distributioner.,

Hvis du er i tvivl og vil se flere artikler om distributioner, skal du skrive i kommentarafsnittet nedenfor. For en mere dybdegående nedskrivning af disse distributioner kan du henvise denne ressource.